Принцип Гюгенца (иллюстрация, геомерическая тень) свет на границе раздела двух сред.
Поляризация света.
Поляризация света
одно из фундаментальных свойств оптического излучения (света), состоящее в неравноправии различных направлений в плоскости, перпендикулярной световому лучу (направлению распространения световой волны). П. с. называются также геометрические характеристики, которые отражают особенности этого неравноправия. Впервые понятие о П. с. было введено в оптику И. Ньютоном в 1704-06, хотя явления, обусловленные ею, изучались и ранее (открытие двойного лучепреломления в кристаллах Э. Бартолином в 1669 и его теоретическое рассмотрение Х. Гюйгенсом в 1678-90). Сам термин "П. с." предложен в 1808 Э. Малюсом. С его именем и с именами Ж. Био, О. Френеля, Д. Араго, Д. Брюстера и др. связано начало широкого исследования эффектов, в основе которых лежит П. с.
Существенное значение для понимания П. с. имело её проявление в эффекте интерференции света. Именно тот факт, что два световых луча, линейно поляризованных (см. ниже) под прямым углом друг к другу, при простейшей постановке опыта не интерферируют, явился решающим доказательством поперечности световых волн (Френель, Араго, Т. Юнг, 1816-19). П. с. нашла естественное объяснение в электромагнитной теории света Дж. К. Максвелла (1865-73) (см. Оптика).
Поперечность световых волн (как и любых др. электромагнитных волн) выражается в том, что колеблющиеся в них векторы напряжённости электрического поля Е и напряжённости магнитного поля Н перпендикулярны направлению распространения волны. Е и Н выделяют (отсюда указанное выше неравноправие) определённые направления в пространстве, занятом волной. Кроме того, Е и Н почти всегда (об исключениях см. ниже) взаимно перпендикулярны, поэтому для полного описания состояния П. с. требуется знать поведение лишь одного из них. Обычно для этой цели выбирают вектор Е.
Световой импульс, испускаемый каким-либо отдельно взятым элементарным излучателем (атом, молекула) в единичном акте излучения, всегда поляризован полностью. Но макроскопические источники света состоят из огромного числа таких частиц-излучателей; пространственная ориентации векторов Е (и моменты актов излучения) световых импульсов отдельных частиц в большинстве случаев распределены хаотически (это не относится, например, к лазерам). Кроме того, поляризация меняется в результате процессов взаимодействия между частицами-излучателями. Поэтому в общем излучении подавляющего большинства источников направление Е не определено (оно непрерывно и беспорядочно меняется за чрезвычайно малые промежутки времени). Подобное излучение называется неполяризованным, или естественным, светом. Е, как и всякий вектор, всегда можно представить в виде суммы его проекций на 2 взаимно перпендикулярных направления (выбираемых в плоскости, поперечной направлению распространения света). В естественном свете разность фаз между такими проекциями непрерывно и хаотически меняется. В полностью поляризованном свете эта разность фаз строго постоянна, т. е. взаимно перпендикулярные компоненты Е когерентны (см. Когерентность). Создав определённые условия на пути распространения естественного света, можно выделить из него поляризованную (полностью или частично) составляющую. Кроме того, полная или частичная (о смысле этого понятия см. ниже) П. с. возникает в ряде природных процессов испускания света и его взаимодействия с веществом.
Полную поляризацию монохроматического света характеризуют проекцией траектории конца вектора Е (рис. 1) в каждой точке луча на плоскость, перпендикулярную лучу. В самом общем случае т. н. эллиптической поляризации такая проекция - эллипс, что легко понять, учитывая постоянство разности фаз между взаимно перпендикулярными компонентами Е и одинаковость частоты их колебаний в монохроматической волне. Для полного описания эллиптической П. с. необходимо знать направление вращения Е по эллипсу (правое или левое), ориентацию осей эллипса и его эксцентриситет (см., например, рис. 2, б, г, е). Наибольший интерес представляют предельные случаи эллиптической П. с. - линейная П. с. (разность фаз 0, kp, где k - целое число, рис. 2, а и д), когда эллипс вырождается в отрезок прямой, и круговая, или циркулярна я, П. с. [разность фаз =(2k + 1)p/2], при которой эллипс поляризации превращается в окружность. Определяя состояние линейно- или плоскополяризованного света, достаточно указать положение плоскости поляризации света, поляризованного по кругу,- направление вращения (правое - рис. 2, в, или левое). В сложных неоднородных световых волнах (например, в металлах или при полном внутреннем отражении) мгновенные направления векторов Е и Н уже не связаны простым соотношением ортогональности, и для полного описания П. с. в таких волнах требуется знание поведения каждого из этих векторов по отдельности.
Если фазовое соотношение между компонентами (проекциями) Е меняется за времена, много меньшие времени измерения П. с., нельзя говорить о полной П. с. Однако может случиться, что в составляющих пучок света монохроматических волнах Е меняется не совершенно хаотически, а между взаимно перпендикулярными компонентами Е существует некоторый преимущественный фазовый сдвиг (фазовая корреляция), сохраняющийся в течение достаточно длительного времени. Физически это означает, что в поле световой волны амплитуда проекции Е на одно из взаимно перпендикулярных направлений всегда больше, чем на другое. Степень подобной фазовой корреляции в таком - частично поляризованном - свете описывают параметром р - степенью П. с. Так, если преимущественный фазовый сдвиг равен 0, свет частично линейно поляризован; = p/2 - частично поляризован по кругу. Частично поляризованный свет можно рассматривать как "смесь" двух крайних видов - полностью поляризованного и естественного. Их соотношение и характеризуют параметром р, который часто (но не всегда) определяют как 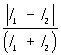 , где индексы 1 и 2 относятся к интенсивностям I света двух "ортогональных" поляризаций, например линейных во взаимно перпендикулярных плоскостях или соответствующих правой и левой круговым поляризациям; р может меняться от 0 до 100%, отражая все количественные градации состояния П. с. (Следует иметь в виду, что свет, проявляющийся в одних опытах как неполяризованный, в других может оказаться полностью поляризованным - с П. с., меняющейся во времени, по сечению пучка или по спектру.)
, где индексы 1 и 2 относятся к интенсивностям I света двух "ортогональных" поляризаций, например линейных во взаимно перпендикулярных плоскостях или соответствующих правой и левой круговым поляризациям; р может меняться от 0 до 100%, отражая все количественные градации состояния П. с. (Следует иметь в виду, что свет, проявляющийся в одних опытах как неполяризованный, в других может оказаться полностью поляризованным - с П. с., меняющейся во времени, по сечению пучка или по спектру.)
В квантовой оптике электромагнитное излучение рассматривают как поток фотонов (см. Излучение, Квантовая механика, Оптика). Состояния П. с. с квантовой точки зрения определяются тем, каким моментом количества движения обладают фотоны в потоке. Так, фотоны с круговой поляризацией (правой или левой) обладают моментом, равным = 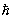 (
( 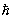 - Планка постоянная). Любое состояние П. с. может быть выражено всего через два т. н. базисных состояния. При описании П. с. выбор пары исходных базисных состояний неоднозначен - ими могут служить, например, любые две взаимно-ортогональные линейные П. с., правая и левая круговые П. с. и т.д., причём в каждом случае от одной пары базисных состояний можно по определённым правилам перейти к др. паре.
- Планка постоянная). Любое состояние П. с. может быть выражено всего через два т. н. базисных состояния. При описании П. с. выбор пары исходных базисных состояний неоднозначен - ими могут служить, например, любые две взаимно-ортогональные линейные П. с., правая и левая круговые П. с. и т.д., причём в каждом случае от одной пары базисных состояний можно по определённым правилам перейти к др. паре.
Эта неоднозначность имеет в квантовом подходе принципиальный характер, однако "произвол" обычно ограничивают конкретные физические условия: наиболее удобно выбирать за базисную пару такие состояния П. с., которые преобладают в актах испускания фотонов элементарными излучателями либо определяют рассматриваемый процесс взаимодействия света и вещества. (Определение состояния П. с. на опыте осуществляется с помощью такого взаимодействия; по общим правилам квантовой механики подобный эксперимент всегда меняет - иногда пренебрежимо мало, иногда существенно - исходную П. с.) Базисные состояния и состояния, описываемые любой линейной комбинацией базисных (суперпозицией, см. Суперпозиции принцип), называются чистыми. Они соответствуют полной П. с., со степенью П. с. 100%. Фотоны могут находиться не только в чистых, но и в т. н. смешанных состояниях, в которых степень их поляризации меньше 100% и может доходить до нуля (естественный свет). Смешанные состояния также выражаются через базисные, но более сложным образом, чем линейная суперпозиция (их называют некогерентной смесью чистых состояний). Взаимодействие света и вещества может в определённых условиях приводить к полному или частичному "выделению" чистых состояний из смешанных (за счёт упомянутого выше изменения П. с. при таком взаимодействии).
Это явление используется для получения полностью поляризованного света или увеличения степени П. с. во многих поляризационных приборах. Если за базисные состояния П. с. выбраны две круговые (правая и левая) П. с., то при их наложении (когерентной суперпозиции) в равных долях наблюдается линейная П. с.; суперпозиции их в различных др. соотношениях дают эллиптические П. с. со всевозможными характеристиками. Через эти же базисные состояния могут быть выражены любые смешанные состояния. Т. о., тот или иной выбор всего двух базисных состояний даёт возможность описать все состояния П. с.
Эксперименты подтверждают теоретический вывод о том, что каждый фотон, поляризованный по кругу, обладает моментом количества движения 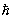 = h/2p (см. Оптическая ориентация, Садовского эффект). Характер поляризации фотонов определяется законом сохранения момента количества движения системы элементарный излучатель - испущенный фотон (при условии, что взаимодействием отдельных излучателей между собой можно пренебречь).
= h/2p (см. Оптическая ориентация, Садовского эффект). Характер поляризации фотонов определяется законом сохранения момента количества движения системы элементарный излучатель - испущенный фотон (при условии, что взаимодействием отдельных излучателей между собой можно пренебречь).
Кроме особенностей элементарных актов излучения, к частичной (а иногда и полной) П. с. приводит множество физических процессов. К ним относятся, например, отражение света и преломление света, при которых П. с. обусловлена различием оптических характеристик границы раздела двух сред для компонент светового пучка, поляризованных параллельно и перпендикулярно плоскости падения (см. Брюстера закон). Свет может поляризоваться при прохождении через среды, обладающие естественной или вызванной внешними воздействиями (индуцированной) оптической анизотропией (вследствие неодинаковости коэффициентов поглощения света при различных состояниях П. с., например при правой и левой круговых П. с. - т. н. круговой дихроизм, являющийся частным случаем плеохроизма; вследствие различия преломления показателей среды для лучей различных линейных поляризаций - двойного лучепреломления, см. также Кристаллооптика). Очень часто полностью поляризовано излучение лазеров; одной из основных (но не единственной!) причин П. с. в лазерах является специфический характер вынужденного излучения, при котором поляризации испускаемого фотона и фотона, вызвавшего акт испускания, абсолютно тождественны; т. о. при лавинообразном умножении числа испускаемых фотонов в лазерном импульсе их поляризации могут быть совершенно одинаковыми. П. с. возникает при резонансном излучении в парах, жидкостях и твёрдых телах. П. с. при рассеянии света столь характерна, что её исследование - один из основных способов изучения как особенностей и условий самого рассеяния, так и свойств рассеивающих центров, в частности их структуры и взаимодействия между собой (см., например, Атмосферная оптика, Комбинационное рассеяние света, Поляризация небесного свода). (При рассеянии поляризованного света происходит и его деполяризация - уменьшение степени П. с.) В определённых условиях сильно поляризовано люминесцентное свечение (см. Люминесценция), особенно при возбуждении его поляризованным светом. П. с. весьма чувствительна к величине напряжённости и ориентации электрических и магнитных полей; в сильных полях компоненты, на которые расщепляются спектральные линии испускания, поглощения и люминесценции газообразных и конденсированных систем, оказываются поляризованными (см. Зеемана эффект. Магнитооптика, Штарка эффект).
Одним из эффектов интерференции поляризованных лучей света является хроматическая П. с.
Характерная для всех интерференционных явлений зависимость от длины волны ("цвета") излучения приводит при этой "П. с." (как показывает само название) к окрашиванию интерференционной картины, если исходный поток был белым светом. Обычная схема получения картины хроматической П. с. в параллельных лучах приведена на рис. 3. В зависимости от разности хода обыкновенного и необыкновенного лучей, приобретаемой в двулучепреломляющей пластинке, наблюдатель видит эту пластинку (в свете, выходящем из анализатора) тёмной или светлой в монохроматическом свете либо окрашенной - в белом. Если пластинка неоднородна по толщине или по показателю преломления, её участки, в которых эти параметры одинаковы, видны соответственно одинаково тёмными или светлыми либо одинаково окрашенными. Линии одинаковой цветности называют изохромами. Схема для наблюдения хроматической П. с. в сходящихся лучах показана на рис. 4, а получаемые при этом картины - на рис. 5.
На многих из перечисленных явлений основаны принципы действия разнообразных поляризационных приборов, с помощью которых не только анализируют состояние П. с., испускаемого внешними источниками, но и получают требуемую П. с. и преобразуют одни её виды в другие.
Особенности взаимодействия поляризованного света с веществом обусловили его исключительно широкое применение в научных исследованиях кристаллохимической и магнитной структуры твёрдых тел, строения биологических объектов (например, поляризационная микроскопия, см. Микроскоп), состояний элементарных излучателей и их отдельных центров, ответственных за квантовые переходы, для получения информации о чрезвычайно удалённых (в частности, астрофизических) объектах. Вообще, П. с. как существенно анизотропное свойство излучения позволяет изучать все виды анизотропии вещества - поведение газообразных, жидких и твёрдых тел в полях анизотропных возмущений (механических, звуковых, электрических, магнитных, световых), в кристаллооптике - структуру кристаллов (в подавляющем большинстве - оптически анизотропных), в технике (например, в машиностроении) - упругие напряжения в конструкциях (см. Поляризационно-оптический метод исследования напряжений) и т.д. Изучение П. с., испускаемого или рассеиваемого плазмой, играет важную роль в диагностике плазмы. Взаимодействие поляризованного света с веществом может приводить к оптической ориентации или т. н. выстраиванию атомов, генерации мощного поляризованного излучения в лазерах и пр. Напротив, исследование деполяризации света при фотолюминесценции даёт сведения о взаимодействии поглощающих и излучающих центров в частицах вещества, при рассеянии света - ценные данные о структуре и свойствах рассеивающих молекул или иных частиц, в др. случаях - о протекании фазовых переходов и т.д. П. с. широко используется в технике, например при необходимости плавной регулировки интенсивности светового пучка (см. Малюса закон), для усиления контраста и устранения световых бликов в фотографии, при создании светофильтров, модуляторов излучения (см. Модуляция света), служащих одними из основных элементов систем оптической локации и оптической связи, для изучения протекания химических реакций, строения молекул, определения концентраций растворов (см. Поляриметрия, Сахариметрия) и мн. др. П. с. играет заметную роль в живой природе. Многие живые существа способны чувствовать П. с., а некоторые насекомые (пчёлы, муравьи) ориентируются в пространстве по поляризованному (в результате рассеяния в атмосфере) свечению голубого неба. При определённых условиях к П. с. становится чувствительным и человеческий глаз (т. н. явление Хайдингера).
Интерференция света.
Это явление наложения волн с образованием устойчивой картины максимумов и минимумов. При интерференции света на экране наблюдается чередование светлых и темных полос, если свет монохроматический (излучаются электромагнитные волны одной длины), или цветных полос, если цвет белый или состоит из волн разной длинны. Необходимым условием наблюдения интерференционной картины является когерентность волн. Два различных источника света не могут быть когерентны. Свет излучается возбужденными атомами, время излучения атома длится ~10-8с, период колебаний, возбуждаемых световой волной ~10-15с. Невозможно согласовать излучение двух атомов одного источника, тем более, невозможно согласовать излучение двух разных источников. Каждый атом излучает короткий цуг волн, который можно представить как сумму монохроматических волн с начальной фазой, определяемой моментом излучения. Поэтому интерферировать могут лишь волны, испускаемые в одном и том же акте излучения. Для получения интерференционной картины видимого света необходимо разделить излучения от одного источника на два потока, эти потоки направить по двум разным траекториям, а затем соединить их в некоторой области пространства. В этом случае в данной точке пространства будут сходиться волны, испущенные одним атомом в одном акте излучения, и разность фаз колебаний, возбуждаемых в этой точке этими волнами, будет определятся только разностью хода волн. Например, луч, падающий непосредственно на экран SA, и луч, отразившийся от зеркала, ОА, будут когерентны. Разность геометрических волн в данном случае является разностью хода волн D=(SO+OA)-SA. Очевидно, что разность хода волн не должна превышать 3 м. Если D>3 м, то в точке A встречаются волны, излученные разными атомами, так как за время 10-8с одним атомом излучается цуг волн длиной l=ct=3 м, где с – скорость света, равная 300000 км/с.
сложение световых волн, при котором обычно наблюдается характерное пространственное распределение интенсивности света (интерференционная картина) в виде чередующихся светлых и тёмных полос вследствие нарушения принципа сложения интенсивностей (см. Интерференция волн). Некоторые явления И. с. наблюдались ещё И. Ньютоном, но не могли быть объяснены с точки зрения его корпускулярной теории (см. Свет, Оптика). Правильное объяснение И. с. как типично волнового явления было дано в начале 19 в. Т. Юнгом и О. Френелем.
И. с. возникает только в случае, если разность фаз постоянна во времени, т. е. волны когерентны (см. Когерентность). До создания лазеров когерентные световые пучки могли быть получены только путём разделения и последующего сведения лучей, исходящих из одного и того же источника света. При этом разность фаз этих колебаний постоянна и определяется только разностью путей, проходимых лучами, или разностью хода D. Существует несколько способов создания когерентных пучков света. Например, в опыте Френеля (рис. 1) два плоских зеркала I и II, образующих двугранный угол, близкий к 180°, дают два мнимых изображения S1 и S2 источника S. На экране AB получается светлая полоса при разности хода D лучей S1M и S2M, равной чётному числу полуволн, и тёмная полоса - при D, равной нечётному числу полуволн. Другой способ был предложен Юнгом (рис. 2). Свет из отверстия S падает на экран AB с двумя отверстиями (или щелями) S1 и S2. И. с. наблюдается на экране CD. Расстояние между соседними светлыми или тёмными интерференционными полосами Dх " l/a, где a - угол S1MS2, под которым сходятся интерферирующие лучи. В этих опытах И. с. наблюдается только при сложении волн, испущенных из одной и той же точки источника. Интерференционные полосы, соответствующие разным точкам источника, сдвинуты относительно друг друга, и при наложении интерференционные картины смазываются. Предельный размер источника, ещё дающего чёткую интерференционную картину, определяется соотношением d = l/b, где b - угол, под которым расходятся лучи из источника (например, ÐS1SS2 на рис. 2).
Это ограничение не имеет места в случае И. с., отражённого от двух поверхностей плоской или слабоклиновидной прозрачной пластинки (рис. 3). При этом между отражёнными лучами возникает разность хода D = 2hn cos i"¢ + l/2, где h - толщина пластинки, n - её показатель преломления, i¢ - угол преломления. Добавочная разность хода l/2 возникает из-за различия сдвига фазы при отражении от верхней и нижней поверхностей пластинки. В строго плоскопараллельных пластинках (с точностью до долей l) одинаковую разность хода будут иметь лучи, падающие на пластинку под одним и тем же углом i, а интерференционные полосы в этом случае называются полосами равного наклона. Они локализованы в бесконечности, поэтому их можно наблюдать в главной фокальной плоскости линзы. В тонких пластинках переменной толщины линии максимумов и минимумов проходят по точкам, соответствующим равной толщине пластинки, и называются полосами равной толщины. Они локализованы в плоскости пластинки. При этом данная интерференционная полоса в монохроматическом свете вычерчивает линию, соответствующую одной и той же толщине пластинки (рис. 4). Если свет не монохроматический, происходит наложение описанных картин для различных длин волн (между собой не интерферирующих); причём положения максимумов и минимумов смещены, поэтому в случае тонкой пластинки наблюдатель видит последовательность цветных полос. Этим явлением И. с. в тонких плёнках объясняются радужная окраска пятен масла или нефти на воде, цвета побежалости на закалённых металлах и др. И. с. в тонких плёнках играет большую роль при просветлении оптики, в интерференциальных светофильтрах, в интерференциальной микроскопии и др. И. с. в тонких плёнках изучается в оптике тонких слоев.
Возможность наблюдения И. с. зависит от степени монохроматичности света. В белом свете можно наблюдать только несколько интерференционных полос вблизи D = 0, которые в этом случае окрашены, потому что положение максимумов и минимумов зависит от длины волны. Если из источника света выделена одна узкая спектральная линия, максимальная разность хода Dmax может достигать нескольких десятков см. Чёткие интерференционные полосы ещё можно наблюдать при Dmax " l2/Dl, где Dl - ширина спектра. Dmax можно связать со временем t, в течение которого фаза волны не сбивается, т. е. излучается волна в виде отрезка синусоиды ("цуг волн"). При этом Dmax оказывается равной длине цуга: Dmax = l2/Dl = ct (c - скорость света), что поясняет невозможность И. с. при D > Dmax, так как соответствующие цуги в двух интерферирующих пучках перестают перекрываться друг другом.
Ограничения размеров источника в приведённых выше опытах снимаются, если источником света служит излучение лазера, которое обладает пространственной когерентностью, и И. с. может наблюдаться при сложении волн, испускаемых разными точками источника. Высокая монохроматичность лазерного излучения позволяет наблюдать И. с. при огромной разности хода.
При очень малых интенсивностях света, когда при помощи чувствительных приёмников регистрируются отдельные фотоны, И. с. проявляется как статистическое явление. Среднее число квантов, попавших на тот или другой участок экрана в течение определённого времени, даёт такое же распределение интенсивности, что и при обычном способе наблюдения. Это находится в полном соответствии с квантовой теорией, согласно которой И. с. происходит не в результате сложения разных фотонов, а в результате "интерференции фотона самого с собой".
И. с. имеет самое широкое применение для измерения длины волны излучения, исследования тонкой структуры спектральной линии, определения плотности, показателей преломления и дисперсионных свойств веществ, для измерения углов, линейных размеров деталей в длинах световой волны, для контроля качества оптических систем и многого другого. На использовании И. с. основано действие интерферометров и интерференционных спектроскопов; метод голографии также основан на И. с.
Важный случай И. с. - интерференция поляризованных лучей (см. Поляризация света). В общем случае, когда складываются две различно поляризованные когерентные световые волны, происходит векторное сложение их амплитуд, что приводит к эллиптической поляризации. Это явление наблюдается, например, при прохождении линейно поляризованного света через анизотропные среды. Попадая в такую среду, линейно поляризованный луч разделяется на 2 когерентных, поляризованных во взаимно перпендикулярных плоскостях луча. Вследствие различного состояния поляризации скорость их распространения в этой среде различна и между ними возникает разность фаз D, зависящая от расстояния, пройденного в веществе. Величина D будет определять состояние эллиптической поляризации; в частности, при D, равной целому числу полуволн, поляризация будет линейной.
Интерференцию поляризованных лучей широко используют в кристаллооптике для определения структуры и ориентации осей кристалла, в минералогии для определения минералов и горных пород, для обнаружения и исследования напряжений и деформаций в твёрдых телах, для создания особо узкополосных светофильтров и др.
Дифракция света.
Явление огибания волнами препятствий и попадания света в область геометрической тени называется дифракцией. Пусть плоская волна падает на щель в плоском экране АВ. Согласно принципа Гюйгенса-Френеля, каждая точка волнового фронта является источником вторичных волн, причем все эти различные источники когерентны. Огибающая к фронтам волн от вторичных источников дает положение нового фронта волны. Явление дифракции наблюдается при условии соизмеримости препятствий с длинной волны l~d. Все вторичные источники когерентны и распределение интенсивности есть результат интерференции волн, излучаемых вторичными источниками.
Дифракционная решетка состоит из чередующихся прозрачных и непрозрачных полос. Суммарная ширина прозрачной и непрозрачной полосы называется периодом дифракционной решетки d. Пусть на решетку падает плоская волна. Так как l~d, то лучи начинают откланяться от первоначального направления распространения. Щели являются когерентными источниками.
Фотоэффект. Фотоэлектрическим эффектом называется испускание электронов с поверхности металла под действием света. Если к электродам откачанной трубки приложить напряжение, ток по цепи не потечет, так как пространстве между катодом и анодом нет носителей тока. Но при облучении катода световым потоком в цепи появится ток. При увеличении напряжения сила тока растет, все большее число электронов, покинувших катод под действием света, достигает анода. Начиная с некоторого значения напряжения U1 сила тока в цепи не изменяется. Это означает, что все электроны, вышедшие из катода за 1 с, достигают анода. Этот ток Iн называется фототоком насыщения. Он позволяет определить количество электронов, покидающих катод за 1 с. При U, равном нулю, фототок отличен от нуля. Это объясняется тем, что электроны вылетают из металлической пластинки с некоторой скоростью и не нужно создавать электрического поля для того, чтобы они достигали анода. Для того, чтобы фототок был равен нулю, надо создать поле, препятствующие движению электронов к аноду. Разность потенциалов, при которой электроны не достигают анода, называется задерживающим напряжением Uз. Изменение кинематической энергии должно быть равно работе электростатических сил поля, созданного между электродами: qeUз=mv2/2, где qe и Uз < 0.
 Рис. 1 Тень винта, окруженная дифракционными полосами Рис. 1 Тень винта, окруженная дифракционными полосами  Рис. 3 Дифракция Фраунгофера на щели Рис. 3 Дифракция Фраунгофера на щели | |
Дифракция света, явления, наблюдающиеся при распространении света мимо резких краёв непрозрачных или прозрачных тел, сквозь узкие отверстия. При этом происходит нарушение прямолинейности распространения света, т. е. отклонение от законов геометрической оптики. Вследствие Д. с. при освещении непрозрачных экранов точечным источником света на границе тени, где, согласно законам геометрической оптики, должен был бы происходить скачкообразный переход от тени к свету, наблюдается ряд светлых и тёмных дифракционных полос (рис. 1 и 2). Поскольку дифракция свойственна всякому волновому движению, открытие Д. с. в 17 в. итальянским физиком и астрономом Ф. Гримальди и её объяснение в начале 19 в. французским физиком О. Френелем явились одним из основных доказательств волновой природы света.
Приближённая теория Д. с. основана на применении Гюйгенса- Френеля принципа. Для качественного рассмотрения простейших случаев Д. с. может быть применено построение зон Френеля. При прохождении света от точечного источника через небольшое круглое отверстие в непрозрачном экране (рис. 2, а) или вокруг круглого непрозрачного экрана (рис. 2, б) наблюдаются дифракционные полосы в виде концентрических окружностей. Если отверстие оставляет открытым чётное число зон, то в центре дифракционной картины получается тёмное пятнышко, при нечётном числе зон — светлое. В центре тени от круглого экрана, закрывающего не слишком большое число зон Френеля, получается светлое пятнышко.
Различают 2 случая Д. с. — дифракция сферической волны, при которой размер отверстия сравним с размером зоны Френеля, т. е.
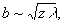
где b — размер отверстия, z — расстояние точки наблюдения от экрана, l — длина волны (дифракция Френеля), и Д. с. в параллельных лучах, при которой отверстие много меньше одной зоны Френеля, т. е.
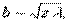
(дифракция Фраунгофера). В последнем случае при падении параллельного пучка света на отверстие пучок становится расходящимся с углом расходимости j ~ l/b (дифракционная расходимость).
Большое практическое значение имеет случай Д. с. на щели. При освещении щели параллельным пучком монохроматического света на экране получается ряд тёмных и светлых полос, быстро убывающих по интенсивности. Если свет падает перпендикулярно к плоскости щели, то полосы расположены симметрично относительно центральной полосы (рис. 3), а освещённость меняется вдоль экрана периодически с изменением j, обращаясь в нуль при углах j, для которых sin j = m/lb (m = 1, 2, 3 ....). При промежуточных значениях освещённость достигает максимальных значений. Главный максимум имеет место при m = 0, при этом sin j = 0, т. е. j = 0. Следующие максимумы, значительно уступающие по величине главному, соответствуют значениям j, определённым из условий: sin j = 1,43 l/b, 2,46 l/b, 3,47 l/b и т.д.
С уменьшением ширины щели центральная светлая полоса расширяется, а при данной ширине щели положение минимумов и максимумов зависит от l, т. е. расстояние между полосами тем больше, чем больше l. Поэтому в случае белого света имеет место совокупность соответствующих картин для разных цветов. При этом главный максимум будет общим для всех l и представится в виде белой полоски, переходящей в цветные полосы с чередованием цветов от фиолетового к красному.
Если имеются 2 идентичные параллельные щели, то они дают одинаковые накладывающиеся друг на друга дифракционные картины, вследствие чего максимумы соответственно усиливаются, а кроме того, происходит взаимная интерференция волн от первой и второй щелей, значительно осложняющая картину. В результате минимумы будут на прежних местах, т.к. это те направления, по которым ни одна из щелей не посылает света. Кроме того, возможны направления, в которых свет, посылаемый двумя щелями, взаимно уничтожается. Т. о., прежние минимумы определяются условиями: b sin j = l, 2l, 3l, ..., добавочные минимумы d sin j = l/2, 3l/2, 5l/2, ... (d — размер щели b вместе с непрозрачным промежутком а), главные максимумы d sin j = 0,l, 2l, 3l, ..., т. е. между двумя главными максимумами располагается один добавочный минимум, а максимумы становятся более узкими, чем при одной щели. Увеличение числа щелей делает это явление ещё более отчётливым (см. Дифракционная решётка).
Д. с. играет существенную роль при рассеянии света в мутных средах, например на пылинках, капельках тумана и т.п. На Д. с. основано действие спектральных приборов с дифракционной решёткой (дифракционных спектрометров). Д. с. определяет предел разрешающей способности оптических приборов (телескопов, микроскопов и др.). Благодаря Д. с. изображение точечного источника (например, звезды в телескопе) имеет вид кружка с диаметром lflD, где D — диаметр объектива, а f — его фокусное расстояние. Расходимость излучения лазеров также определяется Д. с. Для уменьшения расходимости лазерного пучка его преобразуют в более широкий пучок при помощи телескопа, и тогда расходимость излучения определяется диаметром D объектива по формуле j ~ l/D.
