Закон Ома. Сопротивление проводников. См. 3 случая.

Сопротивление проводников

Сопротивление является основной электрической характеристикой проводника.

Сопротивление проводника можно определить из закона Ома:

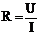
Единица электрического сопротивления в СИ – Ом. Электрическим сопротивлением 1 Обладает такой участок цепи, на котором при силе тока 1 А напряжение равно 1 В.

Опыт показывает, что электрическое сопротивление проводника прямо пропорционально его длине и обратно пропорционально площади поперечного сечения:

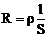Зависимость удельного электрического сопротивления от температуры – см. стр. 16

Постоянный для данного вещества параметр 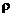называется удельным электрическим сопротивлением вещества. Удельное сопротивление зависит от рода вещества и его состояния (в первую очередь от температуры).

Зависимость сопротивления проводника от температуры.

Если пропустить ток от аккумулятора через стальную спираль, то амперметр покажет уменьшение силы тока. Это означает, что с сопротивлением температуры сопротивление проводника меняется.

Если при температуре, равной 0°С, сопротивление проводника равно R₀, а при температуре t оно равно R, то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры t:

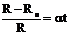(1)

Коэффициент 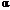называется температурным коэффициентом сопротивления. Он характеризует зависимость сопротивления вещества от температуры.

Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при повышении температура на 1 К.

Для всех металлов 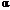>0 и незначительно меняется с изменением температуры. У растворов электролитов сопротивление с ростом температуры не уменьшается, а увеличивается. Для них 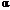<0.

При нагревании проводника его геометрические размеры меняются незначительно. Сопротивление проводника меняется в основном за счет изменения его удельного сопротивления. Можно найти зависимость этого удельного сопротивления от температуры, если в формулу (1) подставить значения

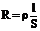и :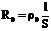

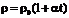
Так как 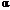мало меняется при изменении температуры, то можно считать, что удельное сопротивление проводника линейно зависит от температуры.

С приближением температуры к абсолютному нулю удельное сопротивление монокристаллов становится очень малым. Этот факт свидетельствует о том, что в идеальной кристаллической решетке металла электроны перемещаются под действием электрического поля, не взаимодействуя с ионами решетки. Электроны взаимодействуют лишь с ионами, не находящимися в узлах кристаллической решетки.

При повышении температуры возрастает число дефектов кристаллической решетки из-за тепловых колебаний ионов, – и это приводит к возрастанию удельного сопротивления кристалла.

Сверхпроводимость

В 1911 г. нидерландский ученый Камерлинг-Оннес обнаружил, что при понижении температуры ртути до 4,1 К ее удельное сопротивление скачком уменьшается до нуля. Явление уменьшения удельного сопротивления до нуля при температуре, отличной от абсолютного нуля, называется сверхпроводимостью. Материалы, обнаруживающие способность переходить при некоторых температурах, отличных от абсолютного нуля, в сверхпроводящее состояние, называются сверхпроводниками.

Прохождение тока в сверхпроводнике происходит без потерь энергии, поэтому однажды возбужденный в сверхпроводящем кольце электрический ток может существовать неограниченно долго без изменения.

Сверхпроводящие вещества уже используются в электромагнитах. Однако получить сколь угодно сильное магнитное поле с помощью сверхпроводящего магнита нельзя, т. к. очень сильное магнитное поле разрушает сверхпроводящее состояние. Поэтому для каждого проводника в сверхпроводящем состоянии существует критическое значение силы тока, превзойти которое, не нарушая сверхпроводящего состояния, нельзя.

Объяснение сверхпроводимости возможно только на основе квантовой теории. Оно было дано лишь в 1957 г.

В 1986 г. была открыта высокотемпературная сверхпроводимость керамик – соединений лантана, бария, меди и кислорода. Сверхпроводимость таких керамик сохраняется до температур около 100 К.