Абсолютно упругий и неупругий удары

1. Удар – кратковременное взаимодействие тел, приводящее к их деформации.

2. При абсолютно упругом ударе возникшие деформации полностью исчезают и тела после удара движутся порознь.

При этом выполняются законы сохранения импульса и кинетической энергии.

Пусть тела массами m₁ и m₂, двигавшиеся со скоростями и соудараются упруго, тогда по закону сохранения импульса 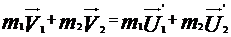, где и 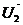- скорости тел после удара, а по закону сохранения кинетической энергии

Решив эти уравнения (с учетом направлений и ), можно получить (для случая, когда ): ;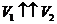

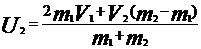
3. При абсолютно неупругом ударе возникшие деформации полностью сохраняются и тела после удара движутся как единое целое. При этом выполняется закон сохранения импульса 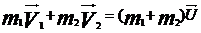, где – скорость совместного движения после удара.

Кинетическая энергия системы не сохраняется, часть суммарной первоначальной кинетической энергии превращается при неупругом ударе в теплоту + Q, где Q - выделяемая теплота.

Решив эти уравнения (с учетом направлений и ) можно получить (для случая, когда ):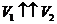

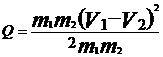
- № 34, 111, 112

ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

1. Момент инерции материальной точки, вращающейся по окружности

радиуса r: – скалярная величина.

Для сплошного тела 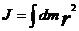, m - масса выделенного бесконечно малого участка.

В случае вращения вокруг оси, проходящей через центр масс тела (центр тяжести) момент инерции равен для:

- цилиндра (диск) 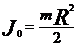, R – радиус основания, ось 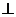основанию;

- шара , R - радиус шара;

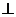- стержня , - длина стержня, ось стержню

2. Теорема Штейнера: 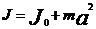, J₀ – момент инерции относительно оси, проходящей через центр масс, J – относительно оси параллельной первой оси и отстоящей на расстоянии а, m – масса

- № 37, 175, 235, 250

3. Момент импульса для материальной точки, вращающейся со скоростью V по окружности радиуса r

, по величине , направление определяется по правилу буравчика.

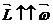Момент импульса для сплошного тела , J – момент инерции, – угловая скорость. Т.о. , т.е. направлена по оси вращения.

4. Момент силы 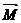- векторная величина , где 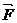– сила, 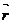– радиус-вектор точки приложения силы (относительно оси вращения). По величине , а направление – правилом буравчика

- № 59

5. II Закон Ньютона для вращательного движения – изменение момента импульса за единицу времени равно моменту силы: или учитывая, что и полагая J=Const, имеем , в случае нескольких сил = +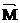

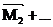
- № 24, 52, 110, 162, 208, 274, 317, 360, 488

6. В замкнутой системе суммарный момент импульса сохраняется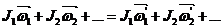

РАБОТА ПРИ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ

При повороте на бесконечно малый угол работа 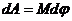, где M -момент силы.

Полная работа , если M=Const, то , где 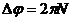, N -число оборотов

- № 9

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА

- при неподвижной оси вращения:

- при движении оси вращения со скоростью V :

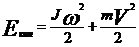, m – масса тела

- № 293, 304

СТАТИКА

Тело находится в равновесии (не перемещается и не вращается), если: а) сумма сил, действующих на тело 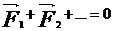; б) сумма моментов сил, действующих на тело + 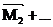= 0

Если при выводе тела из состояния равновесия потенциальная энергия:

а) не изменяется, то равновесие безразличное;

б) увеличивается, то равновесие устойчивое;

в) уменьшается, то равновесие неустойчивое.