Динамика поступательного движения

ГЛОССАРИЙ

по физике для студентов

Технических специальностей

ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ

1. Основные понятия кинематики

- материальная точка – тело, размером и формой которого можно пренебречь при изучении его движения;

- система отсчета – условное или реальное тело, по отношению к которому рассматривается движение данного тела; система отсчета должна быть снабжена устройством для отсчета времени (часы);

- радиус-вектор – вектор, соединяющий начало координат с движущимся телом; 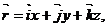где x, y, z - координаты тела;

- вектор-перемещения – вектор, проведенный из начальной точки в конечную: 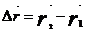, модуль вектора перемещения ;

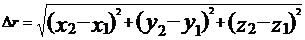- кинематические уравнения – уравнения, описывающие зависимость координат от времени: x=x(t), y=y(t), z=z(t);

- траектория – линия, которую описывает конец радиуса-вектора движущегося тела; чтобы найти уравнение траектории, нужно из кинематических уравнений исключить время.

2. Скорость – векторная величина, характеризующая быстроту движения; 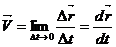– мгновенная скорость; 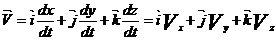, где V_х, V_у, V_z - проекции скорости; модуль скорости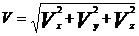

Средняя скорость V_cp= 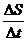, 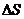- путь, пройденный за время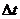

3. Равномерное движение – движение с постоянной скоростью (по величине и направлению), 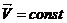(V_x=Const, V_y=Const, V_z=Const). Равномерное движение только прямолинейное. Кинематические уравнения x=V_xt+x_o, y=V_yt+y_o, z=V_zt+z_o, где x_o, y_o, z_o - координаты тела в момент времени t = 0.

Пройденный путь S = Vt.

- № 113, 197, 296, 77, 318

4. Ускорение – векторная величина, характеризующая быстроту изменения скорости 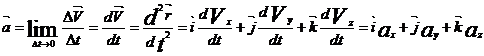; 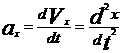- проекция ускорения на ось ОХ, аналогично α_у и α_z.

Модуль ускорения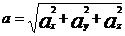

Если а > о, то движение ускоренное, если а < о, то – замедленное. При равномерном движении а = о.

Если движение прямолинейное, то при а > о векторы 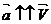, а при а < о векторы .

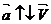5. Равнопеременное движение – движение с постоянным ускорением 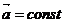(α_х, α_у, α_z – Const).

Формулы для проекций скоростей: V_x=±α_хt+V_ox, V_у=±α_уt+V_oу, V_z=±α_zt+V_oz, где V_ox, V_oу, V_oz – проекции скорости в момент времени t = 0.

Кинематические уравнения: 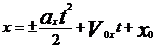, аналогично для y и z.

При прямолинейном движении , .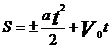

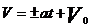6. Свободное падение – движение под действием силы тяжести (частный случай равнопеременного движения).

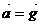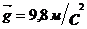Ускорение , где и всегда направлено вертикально вниз.

Если тело падает с некоторой высоты 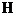с начальной скоростью V_o, направленной вниз, то высота тела над поверхностью земли .

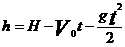Если тело брошено вертикально вверх с начальной скоростью V_o с поверхности земли, то высота движущегося тела над поверхностью земли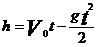

При таком выборе осей координат

Y

0 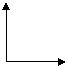x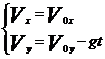

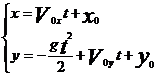
- № 23, 136, 159, 198, 236, 252

7. Равномерное движение по окружности

Линейная скорость 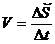, где 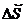– длина дуги, линейная скорость направлена по касательной к траектории.

Угловая скорость 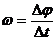, где 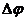– угол поворота радиуса-вектора, угловая скорость направлена вдоль оси вращения (по правилу буравчика).

Так как 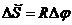, где R - радиус окружности, то между линейной и угловой скоростями связь .

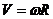Период обращения 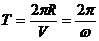– время одного полного оборота.

Частота вращения 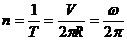– число оборотов за единицу времени.

При равномерном вращении по окружности по величине скорость не изменяется, но изменяется по направлению, т.е. в целом 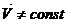, следовательно, тело обладает ускорением, его называют центростремительным (направлено к центру окружности)

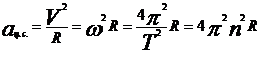
- № 76, 84, 183, 234, 270, 334, 335, 381

8. Ускоренное движение по окружности.

Скорость изменяется как по величине, так и по направлению. Тангенциальное ускорение 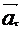характеризует изменение скорости по величине, направлено по касательной к окружности и равно по величине 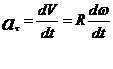. Нормальное ускорение характеризует изменение скорости по направлению, направлено к центру окружности и равно по величине .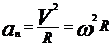

Ясно, что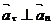

Ускорение 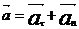называется полным, по величине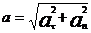

- № 27, 55, 151, 486, 495

9. Угловое ускорение 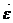характеризует быстроту изменения угловой скорости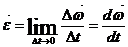

Угловое ускорение, как и угловая скорость направлена вдоль оси вращения. Если вращение ускоренное, то 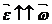, если замедленное, то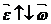

Угловое ускорение связано с тангенциальным .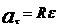

Угловая скорость и угол поворота радиуса-вектора ,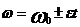

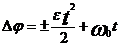
- № 226, 339

ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА

1. Замкнутая система – система тел, взаимодействующих только между собою (действуют только внутренние силы).

2. В замкнутой системе суммарный импульс тел есть величина постоянная – закон сохранения импульса: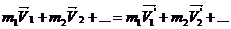

Суммарный импульс сохраняется как по величине, так и по направлению.

3. Координаты центра масс системы материальных точек 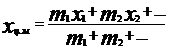; 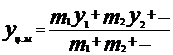, где m_i - массы точек, x_i, y_i - их координаты.

4. В замкнутой системе центр масс сохраняет свое положение

- № 441

СТАТИКА

Тело находится в равновесии (не перемещается и не вращается), если: а) сумма сил, действующих на тело 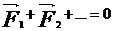; б) сумма моментов сил, действующих на тело + 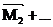= 0

Если при выводе тела из состояния равновесия потенциальная энергия:

а) не изменяется, то равновесие безразличное;

б) увеличивается, то равновесие устойчивое;

в) уменьшается, то равновесие неустойчивое.

ВСЕМИРНОЕ ТЯГОТЕНИЕ

1. Ньютон, 1687, закон: сила тяготения 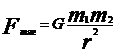, m₁, m₂ – массы, r– расстояние. Гравитационная постоянная 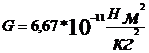есть сила притяжения масс по 1 кг. на расстоянии 1 м. Формула справедлива для материальных точек и тел сферической формы.

2. Ускорение свободного падения (ускорение силы тяжести, напряженность поля тяготения) g – ускорение, сообщаемое телу силой тяготения. По II Закону Ньютона .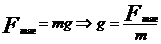

На поверхности Земли 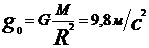, где M, R – масса и радиус Земли.

На высоте h над поверхностью Земли 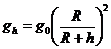, на глубине h под поверхностью Земли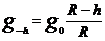

3. Потенциальная энергия тела, поднятого на высоту h над поверхностью Земли, 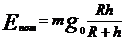(при условии, что на поверхности Земли потенциальная энергия принимается за нуль)

При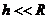

4. I космическая скорость – скорость, которую нужно сообщить телу, чтобы оно стало искусственным спутником Земли (ИСЗ).

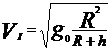, h - высота орбиты над поверхностью Земли

При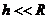

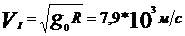
5. II космическая скорость – скорость, которую нужно сообщить телу, чтобы оно преодолело притяжение Земли и удалилось на 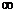(практически попадает в поле притяжения Солнца и становится искусственной планетой)

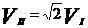, при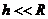

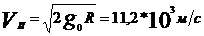
6. III Закон Кеплера – квадраты периодов обращения планет относятся как кубы больших полуосей орбит (планеты движутся по эллипсам)

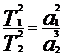, a₁, a₂ – большие полуоси

- № 276

УРАВНЕНИЕ МЕЩЕРСКОГО

1. Рассмотрим движение тела, масса которого в процессе движения изменяется (на примере автомобиля, поливающего водой улицу). Для описания такого движения нужно применить II Закон Ньютона в общем виде:

=

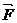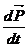
2. Пусть за время dt масса автомобиля изменилась на dm, тогда величина 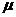= 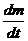называется расходом воды. Обозначим через m и 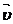массу и скорость автомобиля в данный момент времени, а через 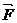силу тяги двигателя автомобиля. Скорость воды, выливающейся из автомобиля, обозначим через .

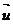Тогда уравнение, описывающее движение автомобиля имеет вид:

m 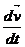= 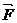- - 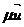уравнение Мещерского

3. Величина (- 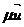) называется реактивной силой, она направлена против направления выброса воды из автомобиля. Она действует до тех пор, пока выбрасывается вода из автомобиля.

ФОРМУЛА ЦИОЛКОВСКОГО

1. Применим уравнение Мещерского для случая движения ракеты. При этом нужно учесть 2 фактора:

а) реактивная сила по величине больше намного всех остальных сил, действующих на ракету, и ими пренебрегают;

б) продукты сгорания топлива выбрасываются не по ходу движения ракеты, а в обратную сторону.

Тогда уравнение Мещерского примет вид:

m= 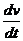= 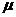u

2. Масса ракеты в процессе движения со временем изменяется:

m=m₀e^-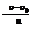

m и m₀ – масса ракеты в данный момент времени и в начальный момент времен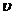и, и 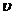₀– скорость ракеты в данный момент времени и в начальный момент времени, u– скорость, с которой продукты сгорания топлива выбрасываются из ракеты.

3. Скорость, которую достигнет ракета через время t после старта, вычисляется по формуле: 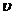= 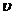₀+u ln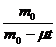, где 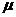- изменение массы ракеты за единицу времени (расход топлива), а остальные обозначения такие же, как и в формуле для массы в пункте 2.

4. Приведенные формулы называются формулами Циолковского.

КОЛЕБАНИЯ И ВОЛНЫ

ВОЛНЫ. БЕГУЩИЕ ВОЛНЫ

1. Волны – распространяющиеся в среде колебания. Частица среды, находящаяся на расстоянии S от источника волн, совершает колебания по закону

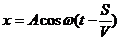– уравнение бегущей волны, 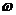- частота колебаний, V - скорость распространения волны. Напомним, что 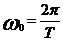, 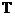– период колебаний

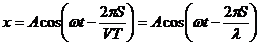, где 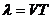- длина волны; 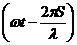– фаза; 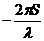– начальная фаза.

2. Фронт волны – геометрическое место точек среды, до которых дошла волна в данный момент времени

Волновая поверхность – геометрическое место точек среды, колеблющихся в одинаковой фазе.

По виду волновой поверхности различают плоские и сферические волны.

Волна называется продольной, если направление колебаний в волне совпадает с направлением распространения волны. Волна называется поперечной, если колебания совершаются в направлении перпендикулярном направлению распространения волны.

3. Когерентные волны – волны, в которых колебания совершаются с одинаковой частотой и в одинаковом направлении, а разность фаз постоянна.

В результате наложения когерентных волн наблюдается интерференция (усиление или ослабление волн)

4. Амплитуда результирующей волны при интерференции 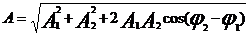, где ₁ и ₂ – амплитуды налагаемых волн, ( ₂ - ₁) – разность фаз волн.

Если ( ₂ - ₁) = 2 nπ, где n= 0, 1, 2..., то = ₁ + ₂, если ( ₂ - ₁) = (2n – 1)π, где n= 1, 2..., то = ₁ - ₂, Первое условие называется условием max, а второе – условием min.

Учитывая, что начальная фаза 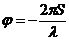, для разности фаз 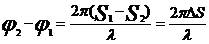, где 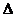S – разность хода волн.

Условия max и min можно выразить через 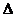S.

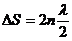– условие max, n=0, 1, 2

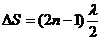– условие min, n=1, 2

- № 19, 68, 70, 263, 331, 416, 481

ГИДРОСТАТИКА

1. Закон Паскаля – давление, оказываемой на жидкость передается по всем направлениям одинаково.

2. Гидростатическое давление – давление, оказываемой жидкостью вследствие силы тяжести.

На глубине h под поверхностью жидкости давление равно 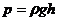, ρ- плотность жидкости.

3. Закон Архимеда: на тело, погруженное в жидкость действует выталкивающая сила, равная весу вытесненной жидкости

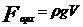, V. – объем вытесненной жидкости

4. Условие плавания тела ρ_T < ρ_Ж, ρ_T и ρ_Ж – плотности тела и жидкости.

ГИДРОДИНАМИКА

1. Идеальная жидкость – несжимаемая жидкость, лишенная вязкости (внутреннего трения).

2. Уравнение неразрывности потока жидкости SV=Const, S – площадь поперечного сечения, V – скорость течения жидкости в данном сечении.

3. Ламинарное течение жидкости – течение жидкости параллельными слоями (траектории частиц жидкости не пересекаются).

4. При турбулентном течении траектории частиц и их скорости хаотично изменяются, движение частиц носит вихревой характер.

5. Уравнение Бернулли для ламинарного течения идеальной жидкости 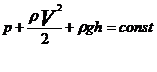, где 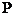– статическое давление, ρqh – гидростатическое давление, 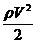– динамическое давление (напор).

6. Сила внутреннего трения между слоями текущей жидкости 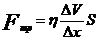, где 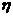– коэффициент вязкости жидкости, S – площадь соприкасающихся слоев, 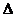V - разность скоростей течения жидкости в слоях, отстоящих друг от друга на расстоянии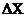

7. Сила сопротивления при движении в жидкости тела сферической формы – формула Стокса

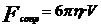, r – радиус шара, V – его скорость.

8. В общем случае сила сопротивления при движении в жидкости (газе) имеет составляющую параллельную направлению движения тела (лобовое сопротивление) и перпендикулярную составляющую (подъемная сила).

9. Формула Пуазейля определяет объем жидкости, протекающий через трубку радиусом R и длиной 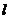за время t

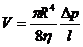, где 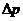– разность давлений на концах трубки

- № 109, 424, 487

ЗАКОНЫ ИДЕАЛЬНЫХ ГАЗОВ

1. Уравнение Клайперана - Менделеева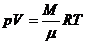

2. Процесс – изменение хотя бы одного из параметров газа. Изопроцесс – процесс, при котором один из параметров остается неизменным

а) изотермический: 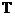=Const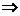 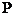V=Const, 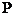₁V ₁ = 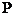₂V ₂

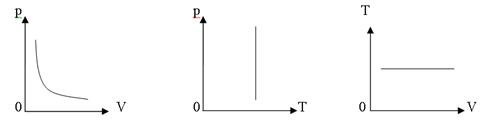
б) изохорный: ,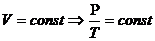

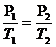
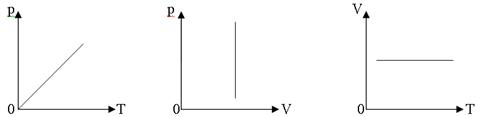
в) изобарный: ,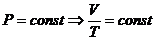

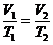
Графики как для изохорного процесса, только вместо 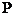будет V, а вместо V будет .

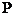3. Разделив обе части уравнения Клайперона – Менделеева на объем 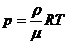, ρ – плотность газа

- № 3, 10, 12, 60, 61, 99, 128, 163, 184, 209, 224, 227, 255, 268, 319, 320, 336, 422

4. Барометрическая формула, описывает изменение концентрации молекул в поле силы тяжести земли

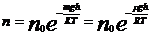
n и n₀– соответственно концентрации молекул на высоте h над поверхностью земли и на поверхности земли

m – масса молекулы, 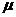– молярная масса, 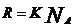– универсальная газовая постоянная

- № 57, 123, 280

5. Распределение Максвелла описывает распределение молекул по скоростям

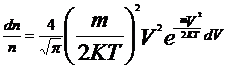- доля молекул, скорости которых лежат в интервале скоростей от V до V+dV.

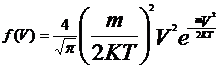- функция распределения.

а) наивероятнейшая скорость 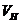– скорость, которой соответствует max функции распределения,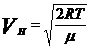

б) средняя арифметическая скорость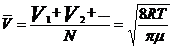

в) средняя квадратичная скорость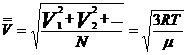

- № 4, 164, 185, 240, 453

ЯВЛЕНИЯ ПЕРЕНОСА

1. Диффузия – процесс взаимного проникновения газов при их соприкосновении, при этом происходит перенос определенной массы вещества

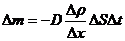– закон Фика, D – коэффициент диффузии, 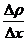- градиент плотности, 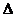S – площадь, 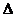t – время, 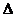m – переносимая масса.

2. Вязкость (внутреннее трение) – процесс переноса импульса между слоями, движущимися с различными скоростями, при этом между слоями возникает сила трения.

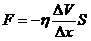– Закон Ньютона, 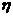– коэффициент вязкости, 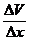– градиент скорости, S – площадь соприкасающихся слоев, F – сила внутреннего трения.

3. Теплопроводность – процесс передачи теплоты в случае неравномерной нагретости тела

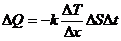– Закон Фурье, k – коэффициент теплопроводности, 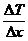– градиент температуры

4. Средняя длина свободного пробега молекул – среднее расстояние, пробегаемое молекулой между двумя последовательными соударениями

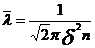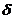, - диаметр молекулы, n – концентрация

5. 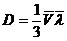, , 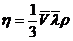, 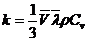где V – средняя арифметическая скорость молекул, ρ - плотность, C_v – удельная теплоемкость при постоянном объеме.

- № 233

ТЕРМОДИНАМИКА

1. Внутренняя энергия U – сумма кинетических энергий движения молекул и потенциальной энергии их взаимодействия (для идеального газа только 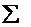E_кин).

Для идеального газа 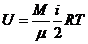, где i=3, 5, 6, изменение внутренней энергии 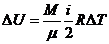зависит только от конечного и начального состояний газа, другими словами U есть функция состояния.

При изотермическом процессе ( 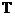=Const) 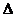U=0.

2. Работа расширения газа при изменении объема на dV равна 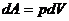, где p - давление

Полная работа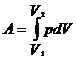

Работа является функцией процесса, т.к. она зависит от того каким образом изменяется объем,

а) при V=Const (изохорный) _v=0, т.к. dV =0

б) при 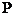=Const (изобарный) _р=p 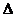V =p(V ₂- V ₁)

в) при 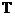=Const (изотермический)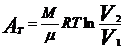

Работа может быть определена графически на диаграмме 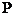V

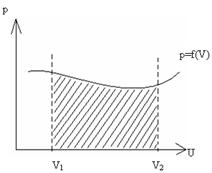
Работа равна численно площади заштрихованной фигуры

3. Количество теплоты, необходимое для нагревания вещества от температуры Т₁ до Т₂

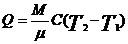или 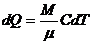, где С – молярная теплоемкость.

Количество теплоты также является функцией процесса, т.к. оно зависит от того каким образом изменяется температура.

а) при V=Const, 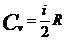, i=3, 5, 6

б) при 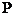=Const, , i=3, 5, 6

в) при 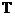=Const, 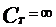, т.к. d 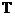=0

- № 79, 98, 177, 464

4. I Закон термодинамики (т/д): теплота подводимая к системе идет на изменение внутренней энергии 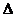U и на совершение работы :

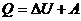или

Правило знаков:

а) если система получает теплоту, то Q>0, если отдает, то Q<0;

б) если внутренняя энергия увеличивается, то 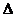U >0, если уменьшается, то 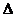U <0;

в) если газ расширяется, то >0, если сжимается, то <0 (работа совершается не газом, а посторонними силами).

5. Применение I Закона термодинамики к изопроцессам:

а) V=Const 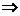=0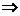

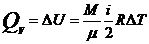
б) 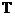=Const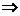 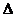U=0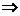

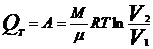
в) 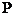=Const: 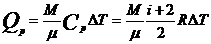, при этом 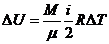, поэтому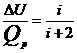

- № 39, 62, 210, 300, 340, 394, 412

6. Адиабатный процесс – процесс, происходящий без теплообмена с окружающей средой (Q=0)

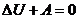или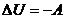

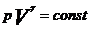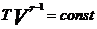Уравнение Пуассона или , где 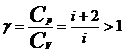– показатель адиабаты.

Теплоемкость адиабатного процесса 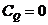(т.к )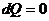

Работа адиабатного процесса 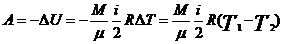, i=3, 5, 6

- № 122, 200, 446

7. Формулировки II Закона термодинамики:

а) теплота не может самопроизвольно передаваться от менее нагретого тела к более нагретому;

б) невозможно построить периодически действующую машину, которая бы совершала работу за счет теплоты, отнятой у наиболее холодного из имеющихся в системе тел («вечный» двигатель II рода).

8. Цикл Карно – цикл, состоящий из чередующихся 2-х изотермических и 2-х адиабатических процессов.

К.п.д. цикла Карно

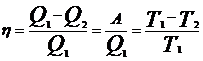, где Q₁ и Q₂ - соответственно теплота, полученная от нагревания и отданная холодильнику, А – работа, производимая за цикл, 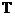₁ и 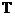₂ – соответственно температура нагревателя и холодильника.

Цикл Карно является идеальным. При заданных 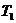и цикл Карно обладает max к.п.д.

- № 11, 40, 41, 124, 133, 139, 238, 257, 282, 305, 306

9. Пусть система перешла из одного состояния в другое получив количества тепла dQ при температуре 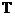, тогда 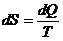– изменение энтропии или 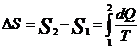, S – энтропия.

Энтропия, как и внутренняя энергия, является функцией состояния, т.е. ее изменение не зависит от того каким путем система перешла из начального состояния в конечное. С учетом I Закона термодинамики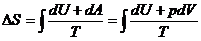

При изотермическом процессе ( 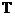=Const) 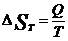, а при адиабатическом процессе (Q=0) 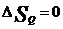, т.е. энтропия при адиабатическом процессе не изменяется (S=Const).

На диаграмме S 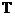цикл Карно выглядит так:

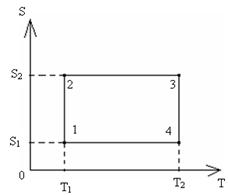
1 2, 3 4 – изотермы

2 3, 4 1 – адиабаты

При обратимом цикле 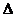S=0 (энтропия не изменяется), при необратимом 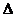S>0 (энтропия увеличивается). Все реальные процессы являются необратимыми, поэтому все реальные процессы приводят к увеличению энтропии.

В равновесном состоянии (все параметры во всех точках одинаковы) энтропия максимальна.

- № 86, 299, 423

10. III Закон термодинамики: абсолютный нуль температуры недостижим (т.е. охлаждая систему невозможно достичь температуры 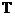= 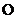⁰ ).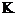

РЕАЛЬНЫЕ ГАЗЫ

1. В уравнение Клайперона-Менделеева необходимо ввести поправки, учитывающие размеры молекул и взаимодействие между ними.

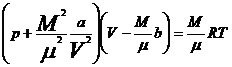- уравнение Ван-дер-Ваальса

a, b - постоянные В-q-В (учет сил взаимодействия – притяжения и размеров молекул – сил отталкивания)

Зависимость 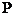от V при постоянном 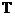на практике графически выглядит так:

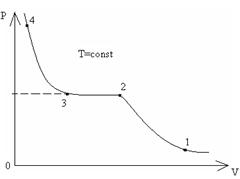
Кривая 12 описывает газообразное состояние, 23 – двухфазное (газ + жидкость), 34 – жидкое состояние вещества

2. С увеличением 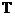ширина горизонтального участка 23 уменьшается, а при некоторой температуре 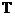_кр превращается в точку перегиба. В таком состоянии исчезает различие между жидкостью и газом. Такое состояние называется критическим. Соответствующее давление и объем также называются критическими.

3. Внутренняя энергия реального газа помимо кинетической энергии движения молекул должна учитывать потенциальную энергию из взаимодействия.

Для реального газа

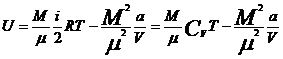
- № 42, 452

ЖИДКОСТИ

1. Вследствие разницы в плотностях жидкости и пара молекулы, находящиеся на поверхности жидкости, испытывают результирующую силу, направленную вглубь жидкости. Поэтому эти молекулы обладают избыточной энергией по сравнению с молекулами, находящимися в объеме жидкости.

По этой причине жидкость принимает такую форму, при которой площадь поверхности минимальна (этим объясняется сферическая форма капель жидкости).

Коэффициентом поверхностного натяжения называется работа, необходимая для увеличения площади поверхности жидкости на единицу .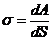

По-другому 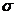можно определить как силу поверхностного натяжения, действующую на единицу длины границы раздела жидкости с другой средой 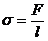, F – сила, – длина границы.

Коэффициент 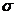зависит от природы жидкости и ее температуры. С увеличением температуры 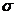уменьшается, а в критическом состоянии 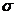=0.

2. Силы поверхностного натяжения стягивают поверхность жидкости, поэтому давление под искривленной поверхностью жидкости больше, чем под плоской поверхностью. Избыточное давление равно 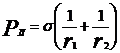– формула Лапласа.

В случае сферической поверхности r₁=r₂ и 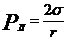, а для цилиндрической поверхности один из радиусов r= 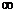и поэтому 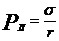, т.е. вдвое меньше, чем при сферической.

3. Из-за избыточного лапласовского давления в тонких трубках (капилляры) жидкость поднимается вверх (смачивающая жидкость) или опускается вниз (несмачивающая жидкость) по сравнению с уровнем жидкости в широкой части сосуда на величину 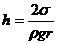, где ρ – плотность жидкости, 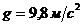, r – радиус капилляра.

ТВЕРДЫЕ ТЕЛА

1. Твердые тела делятся на аморфные и кристаллические. В кристаллах расположение частиц упорядоченное и этот порядок распространяется по всему объему, а в аморфных имеет место ближний порядок, т.е. он нарушается. Аморфные тела изотропны, т.е. их свойства одинаковы во всех направлениях. Кристаллы анизотропны, т.е. их свойства зависят от направления, в котором они рассматриваются.

2. Элементарная ячейка, повторением кото