Стационарное уравнение Шрёдингера

Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда 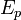не является функцией времени, можно записать в виде:

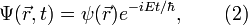где функция 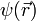должна удовлетворять уравнению:

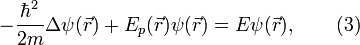
которое получается из уравнения Шрёдингера(1) при подстановке в него указанной выше формулы для 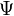(2). Заметим, что это уравнение вообще не содержит времени; в связи с этим оно называется стационарным уравнением Шрёдингера (уравнение Шрёдингера, не содержащее времени).Выражение (2) является лишь частным решением зависящего от времени уравнения Шрёдингера(1), общее решение представляет собой линейную комбинацию всех частных решений вида (2). Зависимость функции 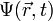от времени проста, но зависимость её от координаты не всегда имеет элементарный вид, так как уравнение (3) при одном выборе вида потенциальной функции 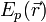совершенно отличается от того же уравнения при другом выборе этой функции. В действительности, уравнение (3) может быть решено аналитически лишь для небольшого числа частных типов функции 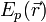.Важное значение имеет интерпретация величины 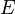в уравнении (2). Она производится следующим путём: временна́я зависимость функции 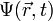в уравнении (2) имеет экспоненциальный характер, причём коэффициент при 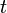в показателе экспоненты выбран так, что правая часть уравнения (3) содержит просто постоянный множитель 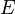. В левой же части уравнения (3)функция 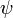умножается на потенциальную энергию 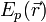. Следовательно, из соображений размерности вытекает, что величина 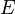должна иметь размерность энергии. Единственной величиной с размерностью энергии, которая постоянна в механике, является полная (сохраняющаяся) энергия системы; таким образом, можно предполагать, что 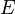представляет собой полную энергию. Согласно физической интерпретации уравнения Шрёдингера, 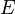действительно является полной энергией частицы при движении, описываемом функцией .

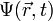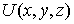16.Трехмерная потенциальная яма. Рассмотрим частицу, находящуюся в трехмерной потенциальной яме с бесконечно высокими стенками (потенциальном ящике). Обозначим через внутреннюю область прямоугольного параллелепипеда (рис.4.6). В данной задаче потенциальная энергия частицы имеет вид

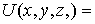
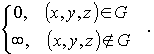
Вне потенциальной ямы волновая функция частицы 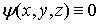. Внутри

Рис. 4.6.

ямы будем, так же как и в двумерном случае, искать волновую функцию в виде произведения

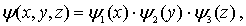
где функция 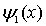зависит только от координаты 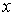, 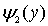- зависит только от , 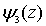- только от .

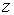Используя тот же самый метод решения, что и для двумерной ямы, из уравнения Шредингера в трехмерном случае получаем три одномерных уравнения

где 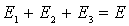. Решение этих уравнений, обращающееся в нуль на границе области 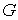, т.е. на непроницаемых стенках потенциального ящика, определяет вид волновой функции частицы

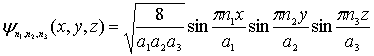(4.26)

и ее энергетический спектр

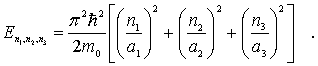(4.27)

Здесь квантовые числа 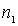, и 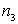принимают значения 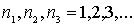. Отметим, что и волновая функция частицы, и ее энергия в случае трехмерной потенциальной ямы зависят от трех квантовых чисел.

Рассмотрим движение частицы в кубической потенциальной яме, т.е. будем считать, что . В этом случае энергетический спектр частицы имеет вид

(4.28)

Энергетические уровни в кубической яме, для которых 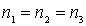, являются невырожденными, все остальные уровни вырождены. Вопрос о кратности вырождения энергетических уровней в кубической яме рассмотрен в задаче 4.4.

Задача 4.3. Частица массы находится в двумерной квадратной потенциальной яме с абсолютно непроницаемыми стенками во втором возбужденном состоянии. Найдите вероятность обнаружения частицы в области 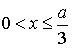, , 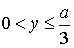где - сторона ямы, а также разность энергий второго и первого возбужденных состояний.

Решение: Волновая функция частицы, находящейся в двумерной квадратной потенциальной яме, согласно (4.23), имеет вид

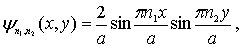
а ее энергетический спектр описывается выражением (4.25)

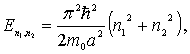
где квантовые числа 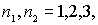.... Первому возбужденному состоянию частицы отвечают квантовые числа 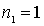, ( или, наоборот, , 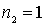) . Следовательно, соответствующий ему энергетический уровень оказывается двукратно вырожденным. Второму возбужденному состоянию соответствуют квантовые числа 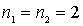, соответствующий ему энергетический уровень невырожден.

Вероятность обнаружить частицу в области 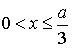, 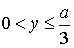определяется выражением

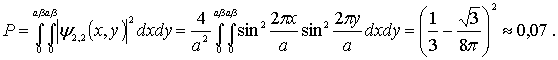
Разность энергий второго и первого возбужденных состояний частицы равна

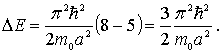
Задача 4.4. Частица массы находится в трехмерной кубической потенциальной яме с абсолютно непроницаемыми стенками. Сторона куба равна . Найдите: а) разность энергий 6-го и 5-го уровней; б) энергию 6-го уровня; в) кратность вырождения 6-го уровня.

Решение: Состояние частицы, находящейся в трехмерной кубической потенциальной яме с абсолютно непроницаемыми стенками, описывается волновой функцией

а энергия частицы, согласно (4.28) , может принимать значения

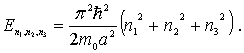
где квантовые числа . Основному состоянию частицы, т.е. состоянию с наименьшей энергией, отвечают квантовые числа . Энергетические уровни возбужденных состояний определяются приведенным выражением для 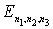при последовательном увеличении суммы квадратов квантовых чисел

Как следует из таблицы, шестому энергетическому уровню соответствует сумма квадратов квантовых чисел, равная четырнадцати, тогда как для пятого уровня эта сумма равна двенадцати. Таким образом, разность энергий шестого и пятого уровней составляет

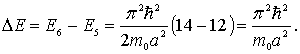
Для энергии шестого уровня получаем

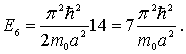
Обсудим теперь вопрос о кратности вырождения энергетических уровней частицы, находящейся в трехмерной кубической яме. Если квантовые числа , 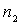и равны между собой, то соответствующий энергетический уровень оказывается невырожденным. Таковы, например, энергетические уровни, отвечающие набору квантовых чисел (1,1,1), (2,2,2) и т.д. Если два из трех квантовых чисел равны между собой, но не равны третьему квантовому числу, то соответствующий энергетический уровень имеет кратность вырождения, равную трем. В частности, трехкратно вырожденными являются второй, третий и четвертый энергетические уровни. И, наконец, если квантовые числа не равны между собой, т.е. если 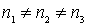, то кратность вырождения определяется числом возможных перестановок из трех чисел, т.е. равна шести. Именно эта ситуация реализуется для шестого энергетического уровня. Таким образом, кратность вырождения шестого уровня .

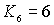Задача 4.5. Нуклон в ядре за счет действия ядерных сил находится в сферической потенциальной яме радиуса 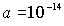м с непроницаемыми стенками. Считая, что основное состояние частицы в поле ядерных сил является сферически симметричным, оцените низший энергетический уровень нуклона в ядре. Массу покоя нуклона считать равной = 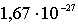кг .

Решение: Ядра атомов состоят из протонов и нейтронов. Эти частицы в ядерном взаимодействии ведут себя одинаковым образом, поэтому и протоны, и нейтроны в ядре называют общим названием - нуклоны.

Мощные короткодействующие ядерные силы удерживают нуклоны в ядре. По условию задачи поле ядерных сил 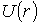в первом приближении можно моделировать сферической потенциальной ямой с непроницаемыми стенками

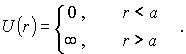
Здесь - расстояние нуклона от центра ядра, а - радиус потенциальной ямы, равный по порядку величины размеру ядра.

Стенки рассматриваемой потенциальной ямы ( ) непроницаемы для частицы из-за бесконечности их энергетической высоты. Поэтому вне ямы, т.е. при 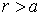, волновая функция нуклона равна нулю. Это означает, что нуклон находится только внутри ямы, где .

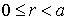Для того, чтобы найти энергию нуклона в сферической потенциальной яме, нужно решить уравнение Шредингера для стационарных состояний

(4.6). С учетом того, что внутри ямы потенциальная энергия нуклона , уравнение Шредингера имеет вид

В силу того, что задача имеет сферическую симметрию, следует перейти в сферическую систему координат и рассматривать волновую функцию как функцию радиальной координаты 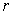и угловых переменных 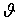и , т.е. 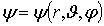. Но поскольку, согласно условию задачи, основное состояние частицы в яме является сферически симметричным, т.е. не зависит от углов 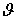и , мы будем считать, что волновая функция частицы зависит только от радиальной координаты . В этом случае оператор Лапласа имеет вид:

Таким образом, уравнение Шредингера для частицы в сферической можно представить в виде

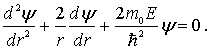
Искомое решение этого уравнения должно удовлетворять двум условиям:

Первое из этих условий является следствием ограниченности волновой функции в любой точке пространства, а второе - следствием непрерывности волновой функции с учетом непроницаемости стенок потенциальной ямы.

Будем искать волновую функцию 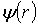в виде 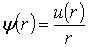. Производные функции 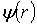по координате есть

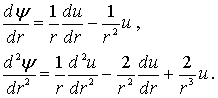
Подставляя их в уравнение Шредингера, получаем уравнение для функции

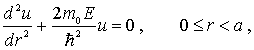
с граничными условиями

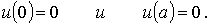
Эта задача формально полностью эквивалентна задаче о движении частицы в одномерной потенциальной яме шириной с бесконечно высокими стенками (см. раздел 4.2 ). Поэтому, с учетом соотношений (4.16), (4.17) , ее решения можно записать в виде

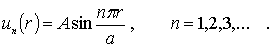
Возвращаясь к функции 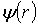, запишем ненормированные ( 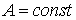) волновые функции

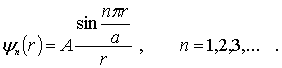
являющиеся решением исходной задачи и описывающие все возможные сферически симметричные квантовые состояния частицы в данной потенциальной яме. Этим квантовым состояниям соответствуют значения полной энергии частицы

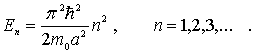
При это выражение определяет минимально возможную полную энергию нуклона в рассматриваемой модели ядра. Подставляя численные значения кг и 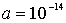м , находим 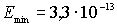Дж =

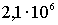эВ = 2,1 МэВ . Это значение энергии значительно превышает энергию электрона в атоме, что указывает на возможность выделения в ядерных процессах энергии, в миллионы раз превышающей энергию химических реакций. Осуществление реакций деления тяжелых ядер и синтеза легких ядер с выделением ядерной энергии подтверждает этот вывод, полученный как следствие законов квантовой механики.