Энергетические соотношения для гармонических колебаний.
59 затух колебания, характеристики, диф ур-е. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ - колебания с постоянно убывающей со временем амплитудой.
Свободные колебания реальных систем всегда затухают. Затухание обусловлено в основном трением (механические системы) и сопротивлением ( в электромагнитных колебательных контурах).
Чем меньше силы трения в системе, тем медленнее затухают колебания, тем лучше колебательная система. Для характеристики качества колебательной системы вводится ряд параметров:
t = 1/b - время релаксации затухающих колебаний (за t амплитуда уменьшается в e раз).
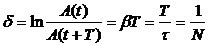 - логарифмический декремент затухания; N - число колебаний, в течение которых амплитуда уменьшается в e раз. Соответственно, exp(bT) - просто декремент затухания.
- логарифмический декремент затухания; N - число колебаний, в течение которых амплитуда уменьшается в e раз. Соответственно, exp(bT) - просто декремент затухания.
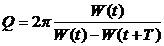 - добротность колебательной системы; W(t) - энергия (полная) колебательной системы в момент времени t.
- добротность колебательной системы; W(t) - энергия (полная) колебательной системы в момент времени t.
Получим дифференциальное уравнение свободных затухающих колебаний на примере реального пружинного маятника, совершающего колебания в среде с сопротивлением (простейший случай - трение о воздух). Пусть масса маятника m, коэффициент упругости пружины k, сила сопротивления, действующая на маятник, F = - bv, v - скорость маятника, b - коэффициент сопротивления среды, в которой находится маятник. Так как мы рассматриваем только линейные системы, b = const, k = const. x - смещение маятника от положения равновесия.
Второй закон Ньютона в нашем случае запишется так:
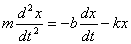
Это уравнение и есть дифференциальное уравнение свободных затухающих колебаний пружинного маятника. Его, однако, принято записывать в следующем, так называемомканоническом виде:
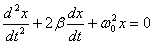
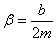 - коэффициент затухания,
- коэффициент затухания, 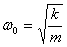 - собственная частота свободных (незатухающих) колебаний пружинного маятника, то, что раньше мы обозначали просто w.
- собственная частота свободных (незатухающих) колебаний пружинного маятника, то, что раньше мы обозначали просто w.
Уравнение затухающих колебаний в таком (каноническом) виде описывает затухающие колебания всех линейных систем; конкретная колебательная система отличается только выражениями для b и j0.
60 математический и физический маятники. Диф уравнение для колебаний физ маятника, решение. Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.
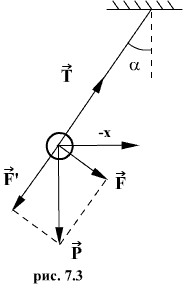
Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая 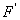 , направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения
, направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения 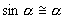 и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
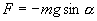
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
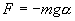
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Момент силы относительно точки О: 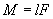 , и момент инерции:
, и момент инерции:
M = FL .
Момент инерции J в данном случае
Угловое ускорение:
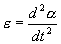
С учетом этих величин имеем:
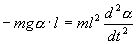
или
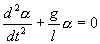 | (7.8) |
Его решение
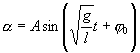 ,
,
где 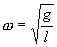 и и 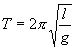 | (7.9) |
Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.
Физический маятник.
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
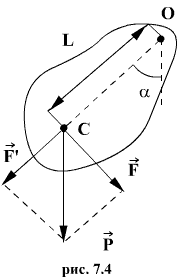
При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
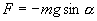
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
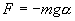
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
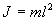 . Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
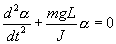 | (7.10) |
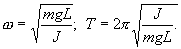 | (7.11) |
Решение этого уравнения
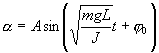
61работа и мощность переменного тока. Коэффициент мощности.нергия, поставляемая источником электродвижущей силы во внешнюю цепь, испытывает превращения в другие виды энергии. Если в цепи имеется только активное сопротивление, то вся энергия превращается в тепло, выделяемое на сопротивлении 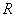 . Между током и напряжением сдвиг фаз отсутствует. Кроме того, в течение малого промежутка времени переменный ток можно рассматривать как постоянный. Поэтому мгновенная мощность, развиваемая переменным током на сопротивлении: При переменном токе различают: активную мощность, кажущуюся мощность и реактивную мощность. Активная мощность (или полезная) вычисляется по формуле:
. Между током и напряжением сдвиг фаз отсутствует. Кроме того, в течение малого промежутка времени переменный ток можно рассматривать как постоянный. Поэтому мгновенная мощность, развиваемая переменным током на сопротивлении: При переменном токе различают: активную мощность, кажущуюся мощность и реактивную мощность. Активная мощность (или полезная) вычисляется по формуле:
P= U*I*cosφ вт,
где φ - угол сдвига фаз между током и напряжением;
cos φ - коэффициент мощности. Он всегда меньше единицы.
Кажущаяся мощность (или полная) определяется выражением:
S= U*I ва.
Полная мощность выражается в вольт-амперах. Эта мощность учитывает активную, или полезную, мощность и реактивную. Реактивная мощность определяется выражением:
Q = U*I*sinφ вар.
Единицей реактивной мощности является вольт-ампер (или киловольт-ампер) реактивный (вар или квар). Активная мощность используется в приемниках тока (моторах, печах, лампах и т. д.), преобразуясь в механическую энергию, тепло и т. п. Реактивная мощность циркулирует между генератором и приемником тока, загружает линии и генератор. Она расходуется на создание и разрушение магнитных (при индуктивной нагрузке) и электрических (при емкостной нагрузке) полей. Чем ниже реактивная мощность, тем лучше используются электрические установки. Уменьшить реактивную мощность можно путем уменьшения сдвига фаз между током и напряжением, т. е. путем увеличения коэффициента мощности (cos φ). Низкий cos φ имеет следствием неполное использование оборудования электрической установки и уменьшение ее коэффициента полезного действия. Задача рационализаторов - добиваться поддержания cosφ установок на достаточно высоком уровне. Cosφ возможно повышать, применяя специальные компенсирующие установки (статические конденсаторы, синхронные компенсаторы) или добиваясь полной загрузки электродвигателей и трансформаторов (см. раздел «Пути экономии электроэнергии»).
62 принцип суперпозиции волн. Волновой пакет.Принцип суперпозиции (наложения) волн заключается в следующем: в линейных средах волны распространяются независимо друг от друга, то есть волна не изменяет свойства среды, и другая волна распространяется так, будто первой волны нет. Это позволяет вычислять итоговую волну как сумму всех волн, распространяющихся в данной среде.
При сложении двух или более синусоидальных волн результирующая волна в общем случае уже не будет синусоидальной.
Рассмотрим в качестве примера результат сложения двух плоских однонаправленных волн с одинаковыми амплитудами и разными, но близкими частотами и волновыми числами:
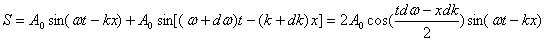
Полученная волна не является синусоидальной, так как величина перед синусом (амплитуда волны) меняется со временем и координатой. Однако, если на длине волны (и в течении периода) её изменения малы (что имеет место при малых dk и dw), волна ещё похожа на синусоиду; её иногда называют квазисинусоидальной. График этой волны представляет собой то, что мы в теории колебаний назвали биениями; однако здесь, в отличие от маятника, биения происходят не только во времени, но и в пространстве.
Волновой пакет — определённая совокупность волн, обладающих разными частотами, которые описывают обладающую волновыми свойствами формацию, в общем случае ограниченную во времени и пространстве. Так, в квантовой механике описание частицы в виде волновых пакетов способствовало принятию статистической интерпретации квадрата модуля волновой функции.[1]
Произвольная отдельная волна 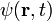 как функция радиус-вектора
как функция радиус-вектора 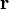 и времени
и времени 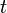 описывается выражением
описывается выражением
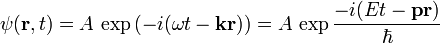
где 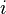 — мнимая единица,
— мнимая единица, 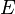 — энергия, переносимая волной,
— энергия, переносимая волной, 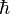 — редуцированная постоянная Планка,
— редуцированная постоянная Планка, 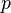 — импульс, переносимый волной,
— импульс, переносимый волной,  — её «круговая» частота (обычная частота, умноженная на
— её «круговая» частота (обычная частота, умноженная на 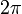 ),
), 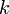 — волновое число (определяемое как
— волновое число (определяемое как 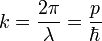 ; здесь
; здесь 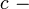 скорость света).
скорость света).
Для волнового описания отдельной частицы, обладающей массой покоя, необходимо просуммировать некоторое количество волн, обладающих близкими частотами,— и в таком случае волновая функция 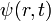 будет заметно отлична от нуля лишь в некоторой, сравнительно небольшой области пространства. Получится волновой пакет.
будет заметно отлична от нуля лишь в некоторой, сравнительно небольшой области пространства. Получится волновой пакет.
Образуем волновой пакет из суперпозиции (набора) плоских волн, для которых волновое число 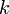 изменяется от
изменяется от 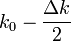 до
до 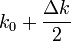 (для простоты предположим, что на имеющем основное значение интервале амплитуды остаются постоянными и равными
(для простоты предположим, что на имеющем основное значение интервале амплитуды остаются постоянными и равными 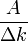 ):
):
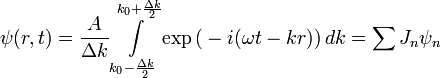
где теперь 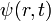 обозначает результирующую волновую функцию, а величины
обозначает результирующую волновую функцию, а величины 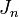 обозначают вклады волн
обозначают вклады волн 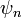 , из которых образован пакет, в результирующую волну, причем
, из которых образован пакет, в результирующую волну, причем 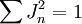 .
.
63 групповая скорость и ее связь с фазовой Итак, в результате суперпозиции нескольких синусоидальных волн образуется несинусоидальная волна с каким-то набором частот и волновых чисел. За скорость распространения такой волны в пространстве берётся скорость распространения фиксированной амплитуды. Но если в случае простой синусоидальной волны эта скорость совпадает со скоростью распространения фиксированной фазы (мы назвали эту скорость фазовой), то в случае сложной несинусоидальной волны сама амплитуда зависит от времени и координат (см. предыдущий пример). Амплитуда сложной волны есть:
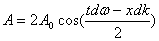
Фиксированная амплитуда А будет удовлетворять условию: 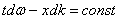
Взяв полный дифференциал от этого выражения, получим (независимые координаты у нас x и t): 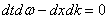
Скорость распространения фиксированной амплитуды в несинусоидальной волне получается следующей:
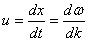
Эта скорость называется ГРУППОВОЙ СКОРОСТЬЮ волны. Она в общем случае отличается от фазовой скорости n:
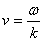
Связь между этими скоростями можно легко получить (учтя зависимость частоты и волнового числа от длины волны):
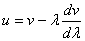
Дисперсия.
