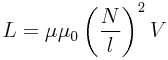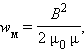Основные теоремы магнитостатики.
| Теорема Гаусса | 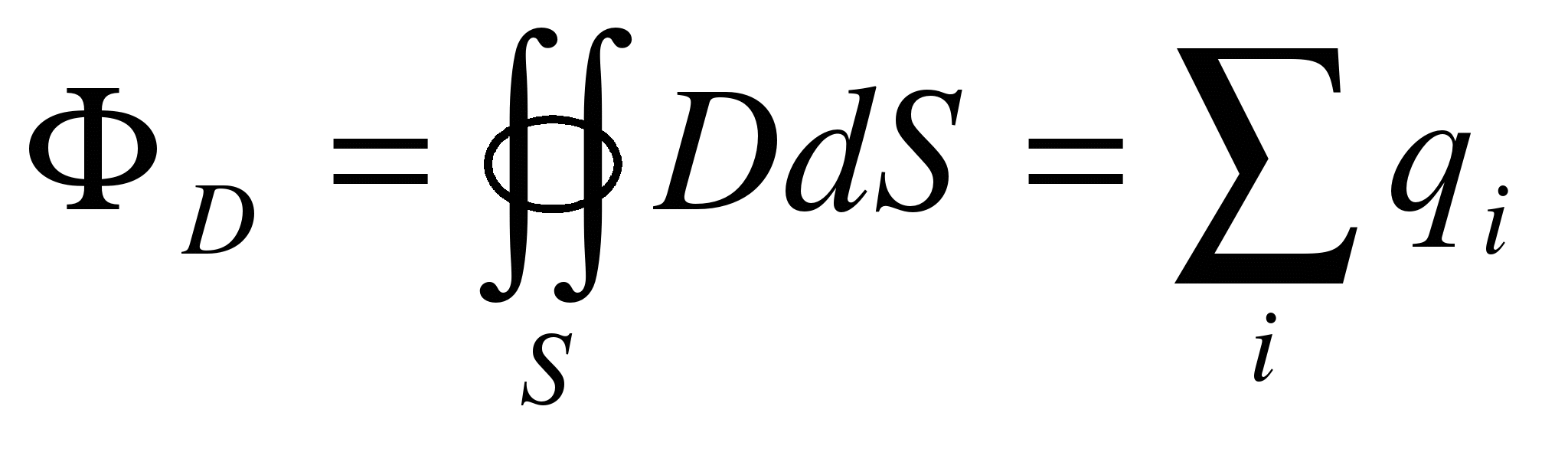 Источники электрического поля - заряды Источники электрического поля - заряды | 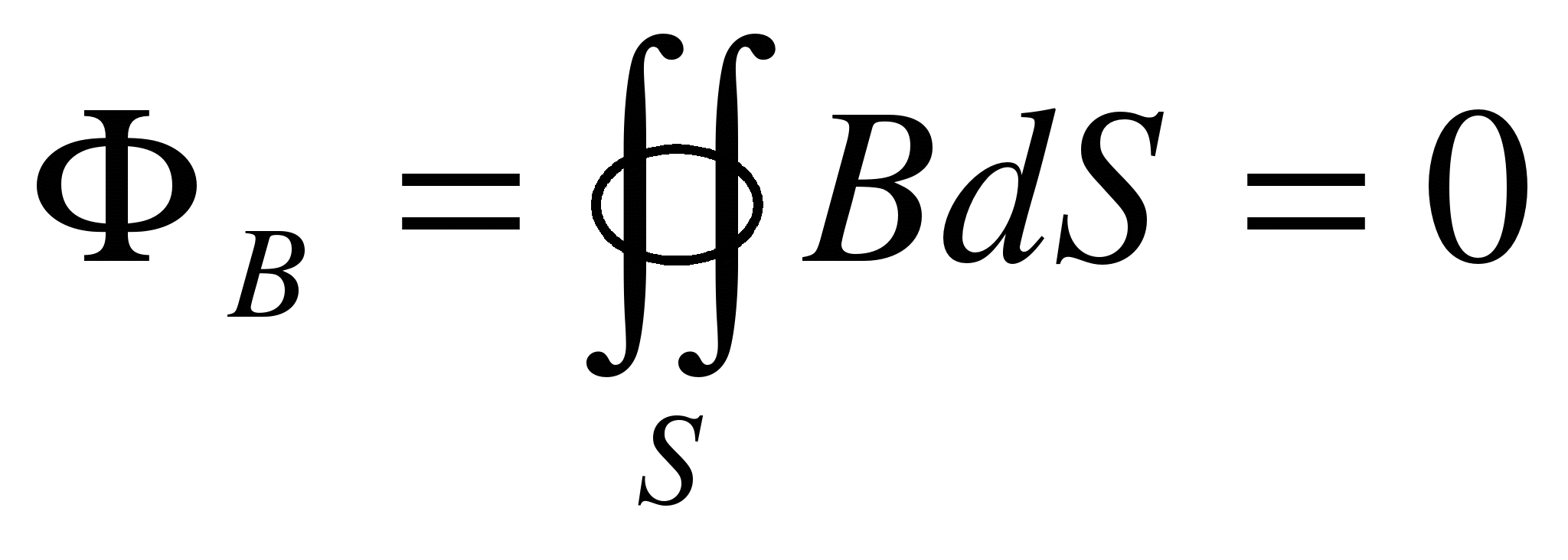 Соленоидальность магнитного поля Соленоидальность магнитного поля |
| ^ Теорема о циркуляции поля |  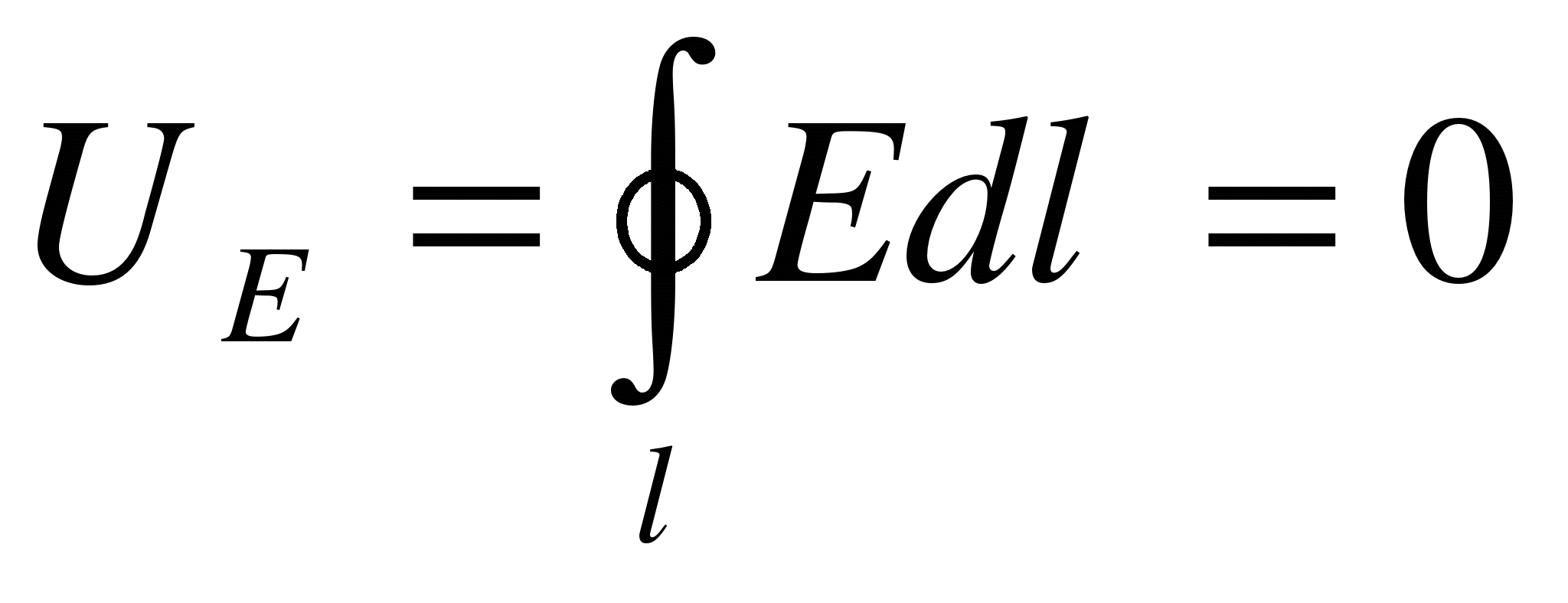 Потенциальность электрического поля Потенциальность электрического поля |  ^ Источники магнитного поля – токи ^ Источники магнитного поля – токи |
| Материальные уравнения |  | 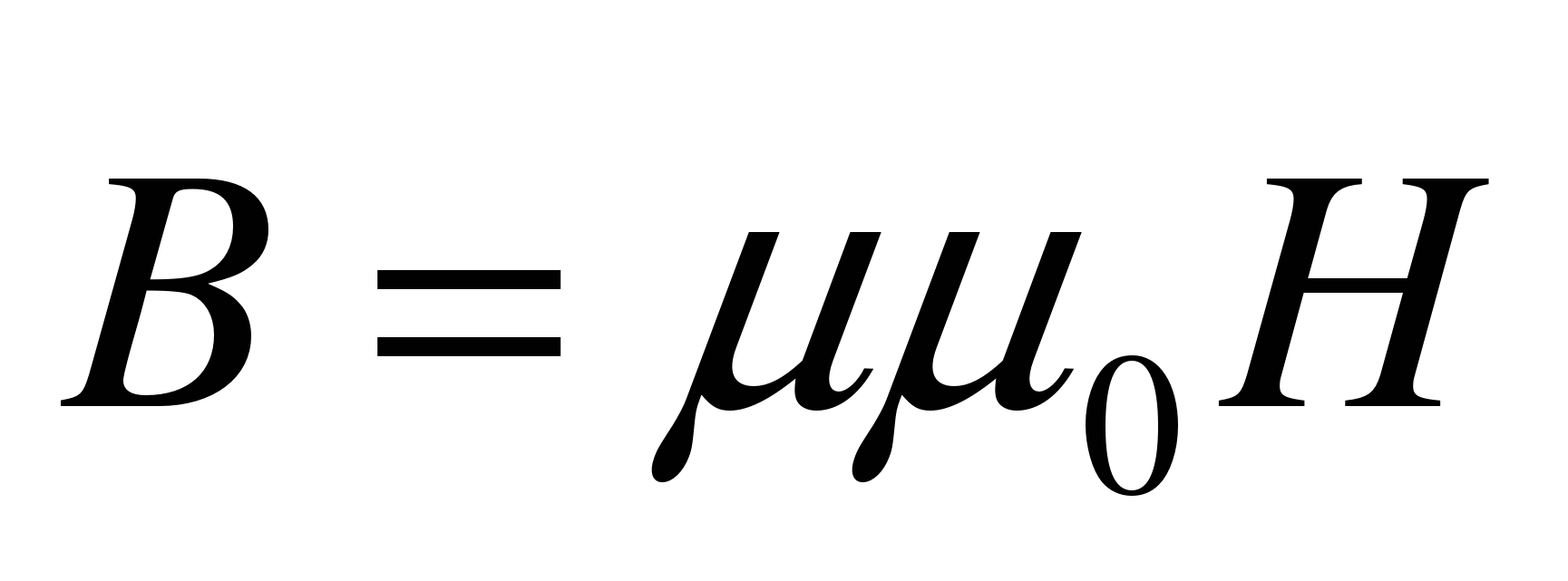 |
46 Магнитное поле соленоида. Соленоидом называют катушку цилиндрической формы из проволоки, витки которой намотаны вплотную в одном направлении, а длина катушки значительно больше радиуса витка.
Магнитное поле соленоида можно представить как результат сложения полей, создаваемых несколькими круговыми токами, имеющими общую ось. На рисунке 3.5 видно, что внутри соленоида линии магнитной индукции каждого отдельного витка имеют одинаковое направление, тогда как между соседними витками они имеют противоположное направление.
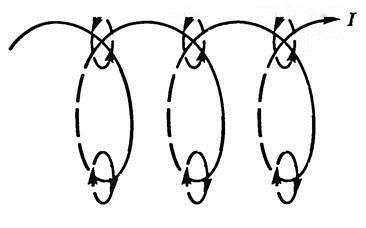
Рис. 3.5. Направление линий магнитной индукции в соленоиде.
Источник: http://www.physbook.ru/images/5/57/Img_T-99-003.jpg
Поэтому при достаточно плотной намотке соленоида противоположно направленные участки линий магнитной индукции соседних витков взаимно уничтожаются, а одинаково направленные участки сольются в общую линию магнитной индукции, проходящую внутри соленоида и охватывающую его снаружи. Изучение этого поля с помощью опилок показало, что внутри соленоида поле является однородным, магнитные линии представляют собой прямые линии, параллельные оси соленоида, которые расходятся на его концах и замыкаются вне соленоида (рис. 3.5).
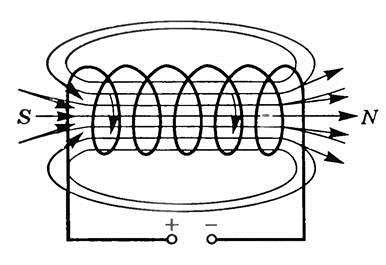
Рис. 3.6. Внутри соленоида магнитное поле однородное.
Источник: http://www.physbook.ru/images/c/c1/Img_T-99-004.jpg
Нетрудно заметить сходство между магнитным полем соленоида (вне его) и магнитным полем постоянного стержневого магнита (рис. 3.6). Конец соленоида, из которого магнитные линии выходят, аналогичен северному полюсу магнита N, другой же конец соленоида, в который магнитные линии входят, аналогичен южному полюсу магнита S.
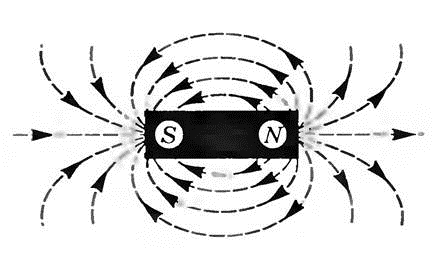
Рис. 3.6. Магнитное поле постоянного стержневого магнита.
Источник: http://www.physbook.ru/images/c/c7/Img_T-99-005.jpg
Полюсы соленоида с током на опыте легко определить с помощью магнитной стрелки. Зная же направление тока в витке, эти полюсы можно определить с помощью правила правого винта: вращаем головку правого винта по току в витке, тогда поступательное движение острия винта укажет направление магнитного поля соленоида, а следовательно, и его северного полюса. Модуль магнитной индукции внутри однослойного соленоида вычисляется по формуле
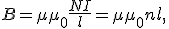
где Ν - число витков в соленоиде, I - длина соленоида, n - число витков, приходящееся на единицу длины соленоида
47 явление самоиндукции.Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.

При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции.

Это явление называется самоиндукцией.
Самоиндукция - явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока.
Возникающая при этом ЭДС называется ЭДС самоиндукции
48 индуктивность. Индуктивность соленоида. Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур.[2][3][4].
В формуле
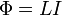
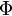 — магнитный поток,
— магнитный поток,  — ток в контуре,
— ток в контуре,  — индуктивность.
— индуктивность.
· Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно - в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока[4]:
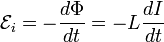 .
.
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током[4]:
 .
.
| Индуктивность соленоида | Магнетизм [ Физика ] | |
|
49 магнитная энергия тока. Объемная плотность энергии.Таким образом, энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна
|
Применим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, можно получить:
 |
где V – объем соленоида. Это выражение показывает, что магнитная энергия локализована не в витках катушки, по которым протекает ток, а рассредоточена по всему объему, в котором создано магнитное поле. Физическая величина
|
равная энергии магнитного поля в единице объема, называется объемной плотностью магнитной энергии. Дж. Максвелл показал, что выражение для объемной плотности магнитной энергии, выведенное здесь для случая длинного соленоида, справедливо для любых магнитных полей.
50 закон максвелла для распределения молекул по скоростям и кинетическим энергиям теплового движения.Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по модулям скоростей. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), скорости которых заключены в этом интервале.
Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, то есть:
dN(v)/N=f(v)dv, откуда f(v)=dN(v)/Ndv (28)
Применяя методы теории вероятностей, Дж. Максвелл нашел вид функции распределения молекул идеального газа по модулям скоростей хаотического движения:
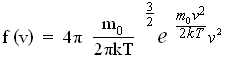 (29)
(29)
Из (29) следует, что конкретное распределение зависит от рода газа (от массы молекулы ) и от его термодинамической температуры. Очевидно, что функция распределения не зависит ни от давления, ни от объема газа. График функции распределения имеет вид, показанный на рис. 5.
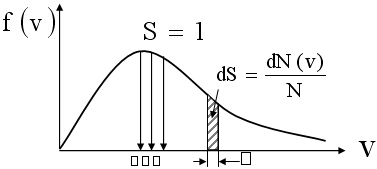
Рис. 5. График функции распределения молекул по скоростям
Выражение dN(v)/N=f(v)dv представляет собой вероятность встретить молекулу со скоростью, принадлежащей интервалу (v;v+dv). Эта вероятность равна площади заштрихованной полоски с основанием dv (рис. 5).
51 УРАВНЕНИЕ МАКСВЕЛЛА1. Первое уравнение Максвелла представляет собой закон Гаусса (да, того самого Карла Гаусса, чьё имя носит колоколообразное распределение случайных величин; в те времена можно было быть и выдающимся математиком и выдающимся физиком одновременно) для электрических полей. Максвелл записал его в дифференциальной форме. В современной записи оно выглядит так (не пугайтесь математики, и не бросайте чтение хотя бы еще несколько абзацев):
∇·E = ρ/εo
где:
E – векторное электрическое поле (здесь и далее жирным шрифтом выделены векторные величины, а курсивом - скалярные);
∇· – значок оператора дивергенции (потока);
ρ – суммарный заряд;
εo – диэлектрическая постоянная вакуума.
Первое уравнение говорит об очевидной вещи…
Но перед тем как ее озвучить, давайте разберемся, что такое дивергенция векторной величины. Вы видели водопроводный кран? Ну, тогда вы хорошо знаете, что такое дивергенция. В переводе с латинского это извержение наружу. Иначе говоря, поток. Для водопроводного крана это поток вытекающей воды, который тем больше, чем больше диаметр трубы и напор воды в ней. Если дивергенция больше нуля, то точка является источником, если меньше – стоком. Теперь вы знаете половину нужной векторной математики.
…Но вернемся к первому уравнению Максвелла (оно же – закон Гаусса). Оно говорит том, что поток электрического поля Е через любую замкнутую поверхность зависит от суммарного электрического заряда внутри этой поверхности. Иначе говоря, если из замкнутого бассейна вытекает воды больше, чем в него втекает (то есть суммарный поток из бассейна получается больше нуля), то ясно, что внутри бассейна прячется труба – источник этой самой воды (иначе бы она быстро кончилась).
С электрическим полем то же самое: если есть электрический заряд (труба-источник воды в бассейне), то поле от него будет вытекать наружу во все стороны (вода будет выливаться через края).
3. Третье (нарушим порядок следования для удобства понимания) уравнение Максвелла – это тоже закон Гаусса, записанный в дифференциальной форме. Но для магнитных полей:
∇·B = 0
где:
B – векторное магнитное поле.
Это уравнение говорит о том, что поток магнитного поля через любую замкнутую поверхность всегда равен нулю. Или, иначе говоря, что одиночных магнитных зарядов в природе не существует. Вот электрически отрицательный электрон и положительный электрически протон есть и могут успешно существовать отдельно друг от друга. А полюса магнита отдельными не бывают. Только вместе. Один такой полюс толкает вперед, другой – тянет назад.
В примере с бассейном это две трубы, разнесенные на какое-то расстояние: сколько по одной втекает, столько по другой и вытекает. Движение воды по кругу у нас есть. Но суммарный поток равен нулю: сколько пришло, столько и ушло. Наружу ничего не вытекает. Точно также как и в потоке магнитного поля через замкнутую поверхность.
2. Второе уравнение Максвелла это закон Фарадея (на всех конденсаторах написано имя Майкла Фарадея) впервые в дифференциальной форме записан Максвеллом в качестве его третьего уравнения:
∇×E = – ∂B/∂t
где:
∇× – значок оператора ротора (вихря);
∂B/∂t – частная производная (изменение) B по времени. Частная в том смысле, что магнитное поле вообще меняется и в пространстве и во времени, но тут нас интересует только его изменение во времени.
Это уравнение говорит, что ротор (интеграл по замкнутому контуру) электрического поля Е равен потоку (т.е. скорости изменения во времени) магнитного поля В сквозь этот контур.
… Тут надо остановиться и разобраться, что такое ротор векторного поля. Вы наблюдали, как вода уходит из ванной в сливное отверстие? Тогда вы этот самый ротор видели: крутящаяся воронка воды вокруг открытой пробки и есть ротор. Точнее говоря, не сама воронка, а сумма (еще точнее –интеграл: ведь любой интеграл это сумма чего-то) векторов угловых скоростей, частиц воды, крутящихся по замкнутому контуру вокруг отверстия пробки. Всё, теперь вы знаете векторную математику на уровне, достаточном для полного понимания Максвелла…
Но вернемся со второму уравнению Максвелла. Там то же самое, что и в ванне: чем больше и чем быстрее изменяется магнитное поле внутри контура (чем сильнее сосёт воду сливное отверстие), тем сильнее раскручивается вихревое электрическое поле (стекающая вода) вокруг этого контура (отверстия).
На законе Фарадея (т.е. на втором уравнении Максвелла) работают все генераторы электричества: механически вращающийся магнит создает изменяющееся магнитное поле внутри катушки, с которой снимается индуцированный электрический ток.
4. Четвертое уравнение Максвелла. Сначала Максвелл взял закон Андре Ампера (которого он называл "Ньютоном электричества", а мы вспоминаем при каждом измерении тока), связывающий постоянный ток и магнитное поле вокруг него:
∇×B = j/εoc2
где:
j – ток;
с – скорость света (на самом деле мы тут забегаем вперед, говоря, что это скорость света. Ни Ампер, ни Максвелл, когда писали свои уравнения этого еще не знали, и называли с2 "электромагнитной постоянной").
Этот закон говорит, что ротор (интеграл от B по замкнутому контуру) равен току, текущему сквозь этот контур. Ну не прямо равен, а с коэффициентом 1/εoc2. Иногда этот коэффициент обозначают как μo и называют магнитной постоянной вакуума. Но это делают только для упрощения записи: μo = 1/εoc2.
52 ток смещенияМаксвелл сделал вывод: всякое переменное электрическое поле порождает переменное магнитное поле.
Токи проводимости в проводнике замыкаются токами смещения в диэлектрике или в вакууме. Переменное электрическое поле в конденсаторе создает такое же магнитное поле, как если бы между обкладками существовал ток проводимости, имеющий величину, равную току в металлическом проводнике.
Это утверждение позволяет (на базе нашего примера с конденсатором) найти величину тока смещения. В свое время мы с вами доказали, что поверхностная плотность поляризационных зарядов σ равна 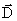 – вектору электрического смещения:
– вектору электрического смещения:
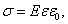

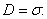 , , | (7.2.2) |
Полный заряд на поверхности диэлектрика и, следовательно, на обкладках конденсатора 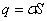 (S – площадь обкладки)
(S – площадь обкладки)

Тогда
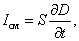 , , | (7.2.3) |
т.е. ток смещения пропорционален скорости изменения вектора электрического смещения 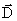 . Поэтому он и получил такое название – ток смещения.
. Поэтому он и получил такое название – ток смещения.
Плотность тока смещения
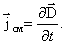 , , |
53 относительность электрических и магнитных полейДавайте подумаем, что произойдет с отрицательным зарядом, движущимся со скоростью v0 параллельно проволоке, покоторой течет ток (фиг. 13.10). Постараемся разобраться в происходящем, используя две системы отсчета: одну, связанную с проволокой, как на фиг. 13.10, а, а другую — с частицей, как на фиг. 13.10, б. Мы будем называть первую систему отсчета S, а вторую S`.
В системе S на частицу явно действует магнитная сила. Сила направлена к проволоке, поэтому, если заряду ничего не мешает, его траектория загнется в сторону проволоки. Но в системе S` магнитной силы на частицу быть не может, потому что скорость частицы равна нулю. Что же, следовательно, она так и будет стоять на месте? Увидим ли мы в разных системах разные вещи? Принцип относительности утверждает, что в системе S` мы увидели бы тоже, как частица приближается к проволоке. Мы должны попытаться понять, почему такое могло бы произойти.
 |
Вернемся к нашему атомному описанию проволоки, по которой идет ток. В обычном проводнике, вроде меди, электрические токи возникают за счет движения части отрицательных электронов (называемых электронами проводимости), тогда как положительные ядерные заряды и остальные электроны остаются закрепленными внутри материала. Пусть плотность электронов проводимости есть р_, а их скорость в системе S есть v. Плотность неподвижных зарядов в системе S есть р + , что должно быть равно р_ с обратным знаком, потому что мы берем незаряженную проволоку. Поэтому вне проволоки электрического поля нет, и сила на движущуюся частицу равна просто
 |
Используя результат, найденный нами в уравнении (13.18) для магнитного поля на расстоянии r от оси проволоки, мы заключаем, что сила, действующая на частицу, направлена к проволоке и равна по величине
54 экстратоки размыкания и замыкания в эл цепяхПри любом изменении силы тока в проводящем контуре возникает э.д.с. самоиндукции, после чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, по правилу Ленца, всегда имеют такое направление, чтобы оказывать сопротивление изменениям тока в цепи, т. е. имеет направление, противоположное току, создаваемому источником. При выключении источника тока экстратоки так же направлены, как и ослабевающий ток. Значит, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.
Исследуем процесс выключения тока в цепи, содержащей источник тока с э.д.с. ξ , катушку индуктивностью L и резистор сопротивлением R . Под действием внешней э. д. с. в цепи течет постоянный ток

(пренебрегаем внутренним сопротивлением источника тока).
В момент времени t=0 отключим источник тока. Ток в катушке индуктивностью L начнет убывать, что приведет к возникновению э.д.с. самоиндукции ξs = -L(dI/dt) оказывающей препятствие, согласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи задается законом Ома I= ξs/R, или
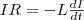 (1)
(1)
Разделив в формуле (1) переменные, получим (dI/I) = -(R/L)dt . Интегрируя эту формулу по I (от I0 до I) и t (от 0 до t), найдем ln (I/I0) = –Rt/L, или
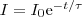 (2)
(2)
где τ = L/R — постоянная, которая называется временем релаксации. Из (2) видно, что τ есть время, в течение которого сила тока уменьшается в е раз.
Значит, в процессе отключения источника тока сила тока уменьшается по экспоненциальному закону (2) и задается кривой 1 на рис. 1. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше τ и, значит, тем медленнее убывает ток в цепи при ее размыкании.
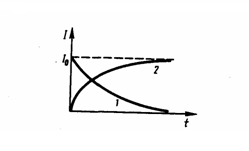
Рис.1
При замыкании цепи помимо внешней э. д. с. ξ возникает э. д. с. самоиндукции ξs = -L(dI/dt) оказывающая препятствие, согласно правилу Ленца, возрастанию тока. По закону Ома, IR = ξ+ξs или
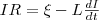
Зададим переменную u = (IR - ξ) преобразуем эту формулу как

где τ — время релаксации.
В момент замыкания (t=0) сила тока I = 0 и u = –ξ . Значит, интегрируя по u и (от –ξ до IR–ξ) и t (от 0 до t), найдем ln[(IR–ξ)]/(–ξ) = -t/τ, или
 (3)
(3)
где I0=ξ/R — установившийся ток (при t→∞).
Значит, в процессе включения источника тока увеличение силы тока в цепи определяется функцией (3) и кривой 2 на рис. 1. Сила тока увеличивается от начального значения I=0 и асимптотически стремится к установившемуся значению I0=ξ/R . При этом, скорость нарастания тока задается тем же временем релаксации τ = L/R, что и убывание тока. Установление тока осуществляется тем быстрее, чем меньше индуктивность цепи и чем больше ее сопротивление.
Оценим значение э.д.с. самоиндукции ξs , которая возникает при мгновенном нарастании сопротивления цепи постоянного тока от R0до R. Допустим, что мы размыкаем контур, когда в нем течет установившийся ток I0=ξ/R . При размыкании цепи ток будет менеться по формуле (2). Подставив в нее формулу для I0 и τ, найдем

Э.д.с. самоиндукции

т. е. при значительном возрастании сопротивления цепи (R/R0>>1), которая обладает большой индуктивностью, э.д.с. самоиндукции может во много раз быть больше э.д.с. источника тока, включенного в цепь. Значит, необходимо учитывать, что контур, который содержит индуктивность, нельзя резко размыкать, так как при этом (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и поломке измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции больших значений не достигнет.
55 гармонические колебания и их характеристики. Диффернециальное уравнение гармонических колебаний. Колебаниями называются движения или процессы, характеризующиеся определенной повторяемостью во времени. Колебательные процессы имеют широкое распространение в природе и технике, например качание маятника часов, переменный электрический ток и т. д. При колебательном движении маятника меняет свое положение координата его центра масс, при переменном токе меняют свои характеристики с определенной повторяемостью напряжение и ток в цепи. Колебательный процесс может имет различную физическую природу, поэтому различают колебания механические, электромагнитные и др. Но различные колебательные процессы характеризуются одинаковыми физическими параметрами и одинаковыми уравнениями. Отсюда вытекает целесообразность единого подхода к исследованию колебаний различной физической природы. Например, единый подход к исследованию механических и электромагнитных колебаний использовался английским физиком Д.У.Рэлеем (1842—1919), русским инженером-экспериментатором П. Н. Лебедевым (1866—1912), А.Г.Столетовым. Большой вклад в развитие теории колебаний сделали Л. И. Мандельштам (1879—1944) и его ученики.
Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на систему, которая совершает колебания. Простейшим типом колебаний являютсягармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Исследование гармонических колебаний важно по двум причинам: 1) колебания, которые встречаются в природе и технике, часто имеют близкий к гармоническому характер ; 2) различные периодические процессы (процессы, которые повторяются через равные промежутки времени) можно представить как суперпозицию (наложение) гармонических колебаний. Гармонические колебания некоторой величины s описываются уравнением вида
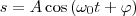 (1)
(1)
где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А.
Определенные состояния системы, которая совершает гармонические колебания, повторяются через промежуток времени Т, имеющий название период колебания, за который фаза колебания получает приращение (изменение) 2π, т. е.

откуда
 (2)
(2)
Величина, обратная периоду колебаний,
 (3)
(3)
т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем

Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса.
Найдем первую и вторую производные по времени от величины s, совершающей гармонические колебания:
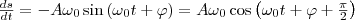 (4)
(4)
 (5)
(5)
т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин в формулах (4) и (5) соответственно равны Аω0 и Аω02 . Фаза величины в формуле (4) отличается от фазы величины в формуле (1) на π/2, а фаза величины в выражении (5) отличается от фазы величины (1) на π. Значит, в моменты времени, когда s=0, ds/dt имеет наибольшие значения; когда же s становится равным максимальному отрицательному значению, то d2s/dt2 равен наибольшему положительному значению (рис. 1).

Рис.1
Из выражения (5) непосредственно вытекает дифференциальное уравнение гармонических колебаний
 (6)
(6)
(где s = A cos(ω0t+φ)). Решением данного дифференциального уравнения является выражение (1).
56 гармонические осцилляторы. Математическим маятником называется идеализированная система, состоящая из невесомой нерастяжимой нити, на которую подвешена масса, сосредоточенная в одной точке (шарик на длинной тонкой нити).
Используйте клавиши, размещенные в панели демонстрационного окна,
для просмотра других изображений и пояснений.
Для доступа к еще одной демонстрации математического маятника подведите курсор к выделенному здесь тексту.
Колебания гармонического осциллятора являются важным примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются: пружинный, математический и физический маятники, а также колебательный контур (для малых токов и напряжений).
Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине с жесткостью k, совершающий гармонические колебания под действием упругой силы (рис. 1.7).
Уравнение движения маятника:
| или . | (1.6.1) |
Из сравнения выражений (1.4.3) и (1.6.1) следует, что пружинный маятник совершает гармонические колебания по закону с циклической частотой ω и периодом Т, где
; .
Рис. 1.7
Эти формулы справедливы для упругих колебаний в пределах, когда выполняется закон Гука, т.е. когда масса пружины мала по сравнению с массой тела и ее деформация не превышает предела упругости.