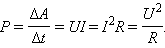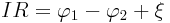Поляризация диэлектриков. Вектор поляризации. (поляризованность).
Диэлектрик, помещенный во внешнее электрическое поле, поляризуется под действием этого поля. Поляризацией диэлектрика называется процесс приобретения им отличного от нуля макроскопического дипольного момента.
Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации (P). Поляризованность определяется как электрический момент единицы объема диэлектрика
,
где N - число молекул в объеме 
. Поляризованность P часто называют поляризацией, понимая под этим количественную меру этого процесса.
28 связь вектора напряженности с вектором смещения. Теорема гаусса для вектора смещения.Напряженность электростатического поля, согласно (88.5), зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна e. Вектор напряженности Е, переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчетах электростатических полей. Поэтому оказалось необходимым помимо вектора напряженности характеризовать поле еще вектором электрического смещения, который для электрически изотропной среды, по определению, равен
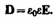(89.1)
Используя формулы (88.6) и (88.2), вектор электрического смещения можно выразить как
(89.2)
Единица электрического смещения — кулон на метр в квадрате (Кл/м2).
Рассмотрим, с чем можно связать вектор электрического смещения. Связанные заряды появляются в диэлектрике при наличии внешнего электростатического поля, создаваемого системой свободных электрических зарядов, т. е. в диэлектрике на электростатическое поле свободных зарядов накладывается дополнительное поле связанных зарядов. Результирующее поле в диэлектрике описывается вектором напряженности Е, и потому он зависит от свойств диэлектрика. Вектором D описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, возникающие в диэлектрике, могут вызвать, однако, перераспределение свободных зарядов, создающих поле. Поэтому вектор D характеризует электростатическое поле, создаваемое свободными зарядами (т. е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.
Аналогично, как и поле Е, поле D изображается с помощью линий электрического смещения, направление и густота которых определяются точно так же, как и для линий напряженности (см. §79).
Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.
Для произвольной замкнутой поверхности S поток вектора D сквозь эту поверхность
где Dn — проекция вектора D на нормаль n к площадке dS.
Теорема Гаусса для электростатического поля в диэлектрике:
(89.3)
т. е. поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.
Для вакуума Dn = e0En (e =1), тогда поток вектора напряженности Е сквозь произвольную замкнутую поверхность (ср. с (81.2)) равен
Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса (81.2) для поля Е в самом общем виде можно записать как
где 
— соответственно алгебраические суммы свободных и связанных зарядов, охватываемых замкнутой поверхностью S. Однако эта формула неприемлема для описания поля Е в диэлектрике, так как она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз доказывает целесообразность введения вектора электрического смещения.
Условия на границе раздела двух диэлектрических сред
Рассмотрим связь между векторами Е и D на границе раздела двух однородных изотропных диэлектриков (диэлектрические проницаемости которых e1 и e2) при отсутствии на границе свободных зарядов. Построим вблизи границы раздела диэлектриков 1 и 2 небольшой замкнутый прямоугольный контур ABCDA длины l, ориентировав его так, как показано на рис. 136. Согласно теореме (83.3) о циркуляции вектора Е,
откуда
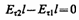
(знаки интегралов по АВ и CD разные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DA ничтожно малы). Поэтому
(90.1)
Заменив, согласно (89.1), проекции вектора Е проекциями вектора D, деленными на e0e, получим
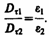(90.2)
На границе раздела двух диэлектриков (рис. 137) построим прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом диэлектрике, другое — во втором. Основания DS настолько малы, что в пределах каждого из них вектор D одинаков. Согласно теореме Гаусса (89.3),
(нормали n и n' к основаниям цилиндра направлены противоположно). Поэтому
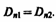(90.3)
Заменив, согласно (89.1), проекции вектора D проекциями вектора Е, умноженными на e0e, получим
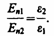(90.4)
Таким образом, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора Е (Еt) и нормальная составляющая вектора D (Dn) изменяются непрерывно (не претерпевают скачка), а нормальная составляющая вектора Е (En) и тангенциальная составляющая вектора D (Dt) претерпевают скачок.
Из условий (90.1) — (90.4) для составляющих векторов Е и D следует, что линии этих векторов испытывают излом (преломляются). Найдем связь между углами a1 и a2 (на рис. 138e1>e2). Согласно (90.1) и (90.4), Еt2 = Еt1 и e2En2 = e1En1. Разложим векторы E1 и E2 у границы раздела на тангенциальные и нормальные составляющие. Из рис. 138 следует, что
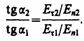
29 распределение заряда на проводнике. Проводник во внешнем электрическом поле. Электростатическая защита. Емкость проводника.Если зарядить изолированный проводник, заряд распределится только на поверхности проводника по следующим причинам:
· поскольку одноимённые заряды отталкиваются, избыточные электрические заряды стремятся расположиться как можно дальше друг от друга; это соответствует распределению заряда на поверхности;
· то же можно доказать с помощью теоремы Гаусса: поля внутри проводника быть не может (иначе заряды ещё бы двигались, и не было бы равновесия), следовательно, и поток поля через любую замкнутую поверхность, построенную внутри проводника, равен нулю; из теоремы Гаусса тогда следует, что внутри проводника нет нескомпенсированных электрических зарядов.
Заряд должен распределиться по поверхности проводника таким образом, что бы эта поверхность была эквипотенциальной. Иначе вдоль поверхности существовало бы электрическое поле, что приводило бы к перемещению зарядов, то есть не было бы равновесия.
Электрическое поле, созданное зарядами на изолированном проводнике, всегда направлено перпендикулярно поверхности проводника. Это поле не приводит к движению зарядов, ибо заряды не могут покинуть проводник (на поверхности металла существует потенциальный барьер, "запирающий" электроны внутри металла, так называемая "работа выхода электрона из металла").
Если внести незаряженный проводник в электрическое поле, то носители заряда приходят в движение. Они распределяются так, чтобы созданное ими электрическое поле было противоположно внешнему полю, то есть поле внутри проводника будет ослабляться. Заряды будут перераспределяться до тех пор, пока не будут выполнены условия равновесия зарядов на проводнике, то есть:
, 
.
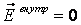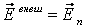Таким образом, нейтральный проводник, внесенный в электрическое поле, разрывает линии напряженности. Они заканчиваются на отрицательных индуцированных зарядах и начинаются на положительных (рис. 2.2).
 |
Если проводник полый, и в полости нет зарядов, то электрическое поле внутри проводника отсутствует, то есть внешние заряды не создают в полости никакого электрического поля. На этом основана так называемая электростатическая защита. Чтобы защитить какое-то тело, например, измерительные приборы, от влияния внешних электростатических полей их окружают проводящей оболочкой. При этом поверхностные заряды располагаются на этой оболочке таким разумным образом, что их поле полностью уничтожает поле внешних источников внутри оболочки.
Электростатическое поле не проникает внутрь проводника, потому что при внесении проводника в электрическое поле оно будет скомпенсировано полем, которое возникает в связи с перемещением свободных зарядов. Электростатическая защита состоит в том, что измерительные приборы помещают в металлические корпуса, чтобы на них не действовали электростатические поля.
Независимо от геометрической формы, которую имеет источник поля (шар, цилиндр, параллельные пластины и т.д.), потенциал поля пропорционален заряду источника. Увеличивая заряд вдвое, мы увеличим вдвое и потенциал. Однако для достижения одного и того же потенциала разным телам требуется разный заряд. Отношение величины заряда уединенного проводника к его потенциалу называется электрической емкостью или просто емкостью уединенного проводника.
,
то есть ёмкость численно равна заряду, сообщение которого проводнику повышает его потенциал на единицу. Если тело имеет большую емкость, то оно может иметь большой электрический заряд при относительно небольшом потенциале. Емкость зависит только от размеров и формы проводника, а также от свойств среды, в которую помещен проводник.
Единицу емкости в системе СИ называют Фарадом. Она названа так в честь Майкла Фарадея. Если при сообщении телу заряда в 1 Кл его потенциал увеличивается на 1 В, то емкость тела равна 1 Ф. Это очень большая емкость. Даже емкость Земли всего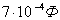 
. Поэтому часто пользуются меньшими единицами емкости: 1 микрофарад (мкФ) = 
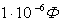или 1 пикофарад (пФ) = 
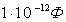. В системе СГС емкость выражается в сантиметрах: 1 Ф = 
.
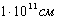30 постоянный электрический ток. Характеристики и условия существования тока. Стационарное электрическое поле, уравнение непрерывности.Металл в твердом состоянии имеет кристаллическое строение. В узлах кристаллической решетки металла расположены положительные ионы, а в пространстве между ними движутся свободные электроны. В обычных условиях в соответствии с законом сохранения заряда металл электрически нейтрален. Если в металле создать электрическое поле, то свободные электроны под действием электрических сил (притяжения и отталкивания) начнут двигаться упорядоченно, т. е. преимущественно в одном направлении. Такое движение электронов называется электрическим током. Скорость движения электронов — до нескольких миллиметров в секунду, а скорость распространения электрического поля 300 000 км/с. Поэтому при создании электрического тока в проводнике все свободные электроны практически одновременно придут в упорядоченное движение.
Если число электронов, проходящих через поперечное сечение проводника, не изменяется со временем, то такой ток называют постоянным. Для создания постоянного тока в проводнике необходимо в нем все время поддерживать электрическое поле. Электрическое поле в проводниках замкнутой электрической цепи создается и поддерживается с помощью источников постоянного тока. Наиболее широкое применение в практике получили гальванические элементы, аккумуляторы, генераторы, солнечные батареи.
В итоге условия существования электрического тока таковы: наличие свободных зарядов, источника тока, потребителя и замкнутой электрической цепи.
Электрический ток возникает не только при упорядоченном движении свободных электронов в металле, но и при упорядоченном движении положительных и отрицательных ионов в растворах электролитов, ионов в газах и т. д.
Электрический заряд частиц, проходящих через поперечное сечение проводника в 1 с, определяет силу тока в цепи, т. е.
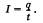
Единица силы тока — ампер (А), но используют и кратные единицы: 1 мА = 10~3 А, 1 кА = = 103 А.
Силу тока в цепи измеряют амперметром.
Электрический ток в замкнутой цепи совершает работу, которая в первую очередь зависит от источника тока, вернее, от его напряжения.
Напряжение показывает, какую работу совершает электрическое поле источника при перемещении единичного положительного заряда из начальной точки в конечную: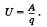 
Единица напряжения — вольт (В), но используют и кратные единицы: 1 мВ = 10~3 В, 1 кВ = = 103 В.
Из стационарности распределения зарядов в поле постоянных токов вытекает, что токи эти необходимо должны быть либо замкнутыми, либо уходить в бесконечность, ибо, в противном
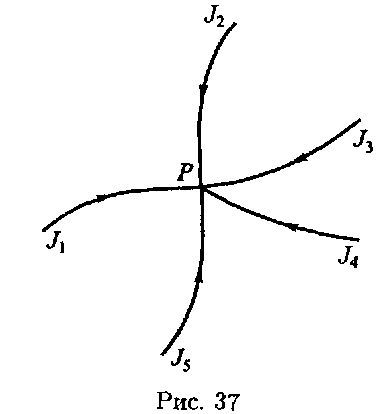
случае, в месте начала (истоков) и окончания (стоков) тока происходило бы с течением времени накопление и убывание зарядов. По той же причине через различные сечения проводника (если только между этими сечениями нет разветвлений проводника) должен протекать ток одинаковой силы. Наконец, в каждой точке Р разветвления цепи тока, в которой соприкасаются между собой два или вообще п проводников, несущих соответственно токи Ji (i = 1, 2, ..., n), должен удовлетворяться так называемый первый закон Кирхгофа, согласно которому алгебраическая
сумма сил токов, притекающих к точке разветвления цепи, должна равняться НУЛЮ:
в противном случае в точке Р происходило бы накопление электрических зарядов. При этом для всех проводников, соприкасающихся в точке Р, положительное направление тока должно быть, конечно, выбрано одинаковым образом, т. е. совпадающим либо с направлением к точке Р, либо с направлением от точки Р (рис. 37). 3. Самое общее условие стационарности токов и поля может быть получено следующим образом. Согласно (36.3) интеграл § jn dS по произвольной замкнутой поверхности S должен равняться алгебраической сумме сил токов, проходящих через отдельные элементы dS этой поверхности, т. е. должен равняться количеству электричества, выходящего за единицу времени из ограниченного поверхностью S объема V (если п есть внешняя нормаль к 5). С другой стороны, согласно лежащему в основе теории электричества закону сохранения электричества ) , количество электричества, вышедшего за 1 с за пределы объема V, должно равняться —de/dt, т. е. убыли за тот же промежуток времени заряда е, находящегося внутри этого объема). Таким образом мы приходим к равенству
Это весьма важное уравнение, по установившейся терминологии, носит название уравнения непрерывности и является математическим выражением постулата сохранения количества электричества. К этому уравнению нам еще придется вернуться в дальнейшем. В интересующем же нас здесь случае постоянных токов распределение зарядов стационарно, т. е. de/dt = 0, так что уравнение непрерывности принимает вид
31 закон ома и джоуля ленца в интегральной и диффернециальной форме.Закон Ома в интегральной форме
Закон Ома для участка электрической цепи имеет вид:
U = RI
где:
U — напряжение или разность потенциалов,
I — сила тока,
R — сопротивление.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:
I=E/(R+r),
где:
e — ЭДС цепи,
I — сила тока в цепи,
R — сопротивление всех элементов цепи,
r — внутреннее сопротивление источника питания.
Закон Ома в дифференциальной форме
Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
j=σ*E
Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов , тогда работу по переносу заряда q на этом участке равна
По определению I= q/t. откуда q= I t. Следовательно 
Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил
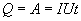 | (17.13) |
Соотношение (17.13) выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности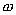 
, равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника
где S - поперечное сечение проводника,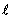 
- его длина. Используя (1.13) и соотношение 
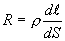, получим
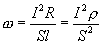
Но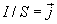 
- плотность тока, а 
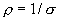, тогда
с учетом закона Ома в дифференциальной форме 
, окончательно получаем
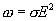 | (17.14) |
Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.
32 работа и мощность тока.При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном учестке совершает работу
| ΔA = (φ1 – φ2) Δq = Δφ12 I Δt = U I Δt, |
где U = Δφ12 – напряжение. Эту работу называют работой электрического тока. Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:
|
33 электрический ток. Сила и плотность тока. Условия существоания тока.Электрический ток - упорядоченное по направлению движение электрических зарядов. За направление тока принимается направление движения положительных зарядов.
Прохождение тока по проводнику сопровождается следующими его действиями:
 | магнитным (наблюдается во всех проводниках) |
| | тепловым (наблюдается во всех проводниках, кроме сверхпроводников) |
| | химическим (наблюдается в электролитах). |
УСЛОВИЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА
Для возникновения и поддержания тока в какой-либо среде необходимо выполнение двух условий:
| | наличие в среде свободных электрических зарядов |
| | создание в среде электрического поля. |
В разных средах носителями электрического тока являются разные заряженные частицы.
1. Сила тока - I, единица измерения - 1 А (Ампер).
Силой тока называется величина, равная заряду, протекающему через поперечное сечение проводника за единицу времени.
I = Dq/Dt.(1)
Формула (1) справедлива для постоянного тока,при котором сила тока и его направление не изменяются со временем. Если сила тока и его направление изменяются со временем, то такой ток называетсяпеременным.
Для переменного тока:
I = lim Dq/Dt , (*)
Dt - 0
т.е. I = q', где q' - производная от заряда по времени.
2. Плотность тока - j, единица измерения - 1 А/м2.
Плотностью тока называется величина, равная силе тока, протекающего через единичное поперечное сечение проводника:
j = I/S.(2)
34 сторонние силы. ЭДС. Обобщенный закон ома.Смещение под действием электрического поля зарядов в проводнике всегда происходит таким образом, что электрическое поле в проводнике исчезает и ток прекращается. Для протекания тока в течение продолжительного времени на заряды в электрической цепи должны действовать силы, отличные по природе от сил электростатического поля, такие силы получили название сторонних сил.
Эти силы могут быть обусловлены химическими процессами, диффузией носителей тока в неоднородной среде, электрическими (но не электростатическими) полями, порождаемыми переменными во времени магнитными полями, и т. д. Всякое устройство, в котором возникают сторонние силы, называется источником электрического тока.
Сторонние силы характеризуют работой, которую они совершают над перемещаемыми по электрической цепи носителями заряда. Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой (ЭДС) 
, действующей в электрической цепи или на ее участке.
| Обобщенный закон Ома для произвольного участка цепи | Электричество [ Физика ] | |
|  | |
| Произведение силы тока на сопротивление участка цепи равно алгебраической сумме падения потенциала на этом участке и ЭДС всех источников электрической энергии, включенных на данным участке цепи. |
