Напряженность Эл.п. Принцип суперпозиции.

Напряженность Эл.п. Принцип суперпозиции.

Взаимодействие между покоящимися зар. осуществляется посредством Эл.п. (электростатического поля) . понятие Эл.п. ввел Фарадей.

Неподвижный Эл.зар. изменяет свойство пространства и создает Эл.п. Оно проявляется по действию на пробный зар. Отношение силы действующей со стороны поля на пробный зар. не зависит от величины этого зар. и может характеризовать само Эл.п. , тогда приходим к характеристике поля – напряженности :

Эл.п. эсть векторная силовая характеристика поля = отношению силы, действующей на зар. со стороны поля,к зар. , т.е.:

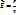q≷0

Напряженность поля численно = силе, действующей на единичный «+» зар. , когда q=+1. Единицы измерения напряжения 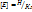или 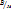, если .

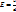Найдем напряжение поля точечного зар. q , находящейся в точке. Хар. вектором в среде, по З.Кулона можем записать

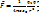
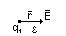
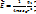- созд. точечный зар.

Если известна Е , то сила со стороны поля действующая на зар. q =:

Сила F, действующая на пробный зар. q в данной точке поля, = векторной сумме сил каждого зар. в отдельности, т.е.:

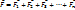, помножим на

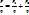… т.е. 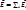- принцип суперпозиции .

Напряженность Эл.п. системы зар. = векторной сумме напряженностей полей, создаваемых каждым зар. в отдельности.

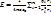
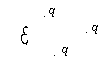
Если непрерывно распределенный зар. т.е.

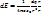
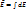
Эл.п. графически изображается с помощью линий напряженности Е, силовых линий, линий Е, метод предложил Фарадей.

Линии напряженности это кривые, касательный к которым в каждой точке совпадают с направлением вектора напряженности в данной точке.

Линии напряженности начинаются на «+» зар. и заканчиваются на «-» или уходят в . Густота силовых линий ,т.е. число линий на ед. площади поверхности перпендикулярной к линиям. Она выбирается так, что количество линий пронизывающих ед. площади поверхности равно или пропорционально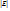

По силовым линиям можно судить о величине и направлении вектора в разных точках пространства. Рассмотрим примеры силовых линий:

Эл.п. называется однородным , если 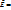const, такое поле реализуется в конденсаторе.

Био-Савара-Лапласа

З-н БСВ даёт выражение для магнитной индукции d , создаваемой элементом I d в точке, характеризуемой радиус-вектором , проведённым из элемента проводника d в искомую точку.

З-н БСЛ

d = [d , ]
µ₀ — магнитная постоянная=4π·10^-7 Гн/м

µ — магнитная проницаемость среды

Модуль индукции |dB|

d =

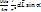
Наряду с магнитной индукцией , можно характеризовать напряжённость магнитного поля .

Дл изотропного случая:

З-н БСЛ для напряжённости d принимает вид:

d = [H]=

З-н БСЛ совместно с принципом суперпозиции допускает в принципе вычисление магнитных полей любой конфигурации токов.

Дифракция света

- явление отклонения света от прямолинейного распространения, проявляющегося в огибании светом препятствий и захождении света в область геометрической тени при прохождении отверстия. Размеры препятствий соизмеримы с длиной волны.

Различают дифр-ю Фраунгофера и Френеля в сходящихся лучах. Начальные закономерности устанавливаются с помощью принципа Гюгенса-Френеля, по которому любая точка фронта волны, до которой дошли колебания является источником вторичных волн и поверхность, которую огибают эти вторичные волны есть фронтовой фронт.

Метод зон Френеля Френель предложил метод разбиения фронта волны на кольцевые зоны, который впоследствии получил название метод зон Френеля.

Пусть от источника света S распространяется монохроматическая сферическая волна, P - точка наблюдения. Через точку O проходит сферическая волновая поверхность. Она симметрична относительно прямой SP.

Разобьем эту поверхность на кольцевые зоны I, II, III и т.д. так, чтобы расстояния от краев зоны до точки P отличались на l/2 - половину длины световой волны. Это разбиение было предложено O. Френелем и зоны называют зонами Френеля.

Возьмем произвольную точку 1 в первой зоне Френеля. В зоне II найдется, в силу правила построения зон, такая соответствующая ей точка, что разность хода лучей, идущих в точку P от точек 1 и 2 будет равна l/2. Вследствие этого колебания от точек 1 и 2 погасят друг друга в точке P.

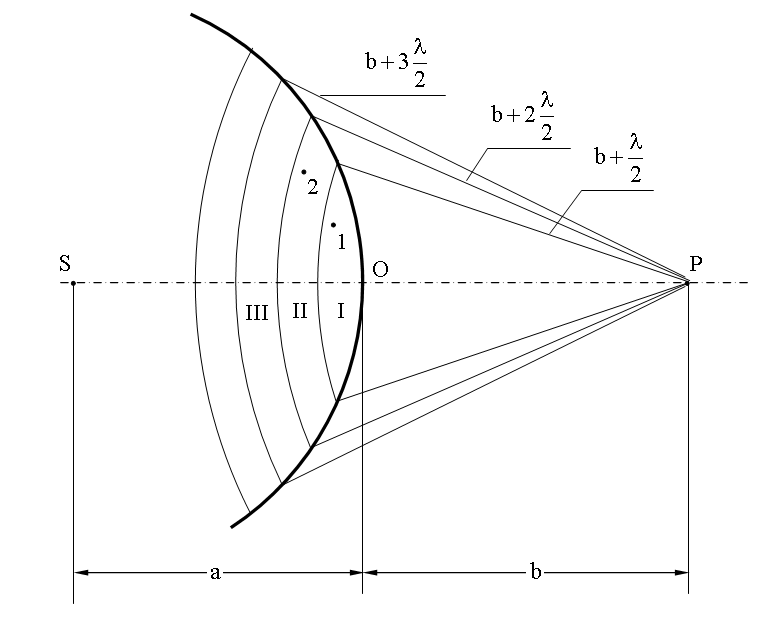
_{Из геометрических соображениях следует, что при не очень больших номерах зон их площади примерно одинаковы. Значит каждой точке первой зоны найдется соответствующая ей точка во второй, колебания которых погасят друг друга. Амплитуда результирующего колебания, приходящего в точку P от зоны с номером m, уменьшается с ростом m, т.е.}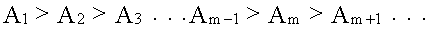

25.Дифракция Фраунгофера на одной щели. Дифракционная решётка.

. За щелью расположена линза Л, в фокальной плоскости которой находится экран Э. Наличие линзы равносильно тому, что экран расположен как бы на "бесконечном" расстоянии от объекта. Если бы свет распространялся прямолинейно в соответствии с законами геометрической оптики, то в фокальной плоскости линзы получилась бы бесконечно узкая светлая полоса, проходящая через точку N0 на экране Э. Но в соответствии с принципом Гюйгенса-Френеля каждая точка волнового фронта, достигающего плоскости, где расположена щель, является источником вторичных волн. Тогда лучи, идущие от всех этих вторичных источников под некоторым углом j к первоначальному направлению, образуют плоский волновой фронт и соберутся в фокальной плоскости линзы в т.Nj

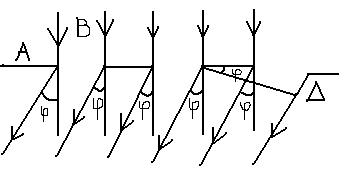
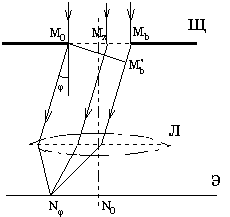
Дифракционная решётка.Простейшая дифракционная решётка представляет собой систему параллельных щелей, разделённых одинаковыми непрозрачными промежутками.

d=a+b-постоянная дифракционной решетки.

На Д.Р. имеют место два явления: дифракция света на каждой щели и интерференция света от всех щелей. Условие, определяющее главные максимумы интенсивности для дифракционной решётки, имеет вид:

dsinφ=κλ

где к=0, ±1,±2….

к-порядок спектра, φ-угол дифракции, λ-длина волны света.

Максимум нулевого порядка один, а максимумов 1-ого,2-ого.3-ого и т.д. порядок по два.

Положения главных максимумов , кроме нулевого, зависит от длины волны. Поэтому при пропускании через решётку белого света все максимумы, кроме центрального, разлагаются в спектр, фиолетовый конец которого обращён к центру дифракционной картинки.

Т.о. дифракционная решётка является спектральным прибором.

Для нулевого порядка для любой длины волны дифракционный угол φ=0 . Поэтому нулевом порядке белый свет не разлагается в спектр.

27.Дисперсия света.

Дисперсия – это совокупность явлений, обусловленная зависимостью показателя преломления n от длины волны λ или от частоты ν (n=n(λ), n=n(ν)).

Дисперсией обусловлено разложение белого света в спектр при прохождении через призму.

Дисперсия нормальная, если с ростом λ показатель убывает.

Нормальная: dn/dλ<0, dn/dν>0

Аномальная: dn/dλ>0, dn/dν<0

Аном. дисперсия наблюдается в областях сильного поглощения света.

Для изучения дисперсии применяется метод скрещивающихся призм.

Полное объяснение дисперсии возможно только в квантовой механике.

В электронной теории для объяснения дисперсии рассматриваются силы прохождения:

1) обобщенная сила Лоренца:

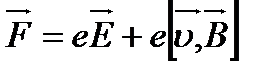
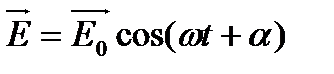
2) сила наподобие силы Гука (обусловлена колебаниями электрона в атоме)

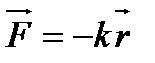, k=mω²

3) сила наподобие силы трения: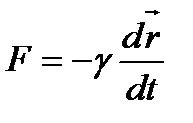

Уравнение движения электрона:

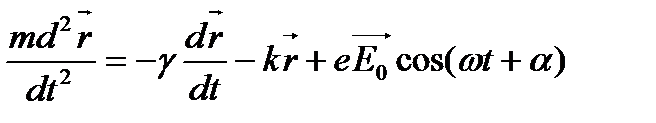
Эффект Холла.

Эффе́кт Хо́лла— явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле.

В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле B течёт электрический ток под действием напряжённости E. Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.

Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска и положительного возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов E1 не скомпенсирует магнитную составляющую силы Лоренца:

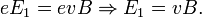
Скорость электронов v можно выразить через плотность тока:

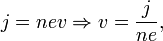
где n — концентрация носителей заряда. Тогда

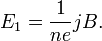
Коэффициент 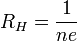пропорциональности между E1 и jB называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак RH, что объясняется в полуклассической и квантовой теориях твёрдого тела.

Дефект массы.

Измерения масс ядер показывают, что масса ядра (Мя) всегда меньше суммы масс покоя слагающих его свободных нейтронов и протонов.

При делении ядра: масса ядра всегда меньше суммы масс покоя образовавшихся свободных частиц.

При синтезе ядра: масса образовавшегося ядра всегда меньше суммы масс покоя свободных частиц, его образовавших.

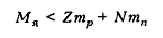
Дефект масс является мерой энергии связи атомного ядра.

Дефект масс равен разности между суммарной массой всех нуклонов ядра в свободном состоянии и массой ядра:

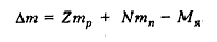
где Мя – масса ядра ( из справочника)

Z – число протонов в ядре

mp – масса покоя свободного протона (из справочника)

N – число нейтронов в ядре

mn – масса покоя свободного нейтрона (из справочника)

Уменьшение массы при образовании ядра означает, что при этом уменьшается энергия системы нуклонов.

Я́дерная реа́кция — процесс образования новых ядер или частиц при столкновениях ядер или частиц.

Законы сохранения:

1. Закон сохранения энергии.Если Е1. Е2. Е3. Е4— полные энергии двух частиц до реакции и после реакции, то на основании закона сохранения энергии: Е1+Е2=Е3+Е4.

2. Закон сохранения импульса

Полный импульс частиц до реакции равен полному импульсу частиц-продуктов реакции. Если р1 р2 р3 р4— векторы импульсов двух частиц до реакции и после реакции, то р1+р2=р3+р4

Шредингера(стационарная).

Статистическое толкование волн де Брой-ля и соотношение неопреде­ленностей Гейзенберга при­вели к выводу, что уравнением движения в квантовой механике, описывающим дви­жение микрочастиц в различных силовых полях, должно быть уравнение, из которо­го бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное урав­нение должно быть уравнением относи­тельно волновой функции 4^е (х, у, г, /), так как именно она, или, точнее, величина l^l², определяет вероятность пребывания частицы в момент времени t в объеме dV, т. е. в области с координатами х и х-\-Ах, уи y-\-dy, г и z + dz. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть во­лновым уравнением,подобно уравнению, описывающему электромагнитные волны. Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером. Уравнение Шредингера, как и все основные уравне­ния физики не выводится, а постулируется. Правиль­ность этого уравнения подтверждается со­гласием с опытом получаемых с его по­мощью результатов, что, в свою очередь, придает ему характер закона природы. Уравнение Шредингера имеет вид

Ψ=Ψ₀cos(ωt-kx) – формула бегущей волны

Ψ= Ψ₀cos1/h(Et-px) – волновая функция фотона

Уравнение Шредингера

v²Ψ+2m/h(E-П)Ψ=0 – для стационарных постоянных

v²=d²Ψ/dx²+ d²Ψ/dy²+ d²Ψ/dz²

Напряженность Эл.п. Принцип суперпозиции.

Взаимодействие между покоящимися зар. осуществляется посредством Эл.п. (электростатического поля) . понятие Эл.п. ввел Фарадей.

Неподвижный Эл.зар. изменяет свойство пространства и создает Эл.п. Оно проявляется по действию на пробный зар. Отношение силы действующей со стороны поля на пробный зар. не зависит от величины этого зар. и может характеризовать само Эл.п. , тогда приходим к характеристике поля – напряженности :

Эл.п. эсть векторная силовая характеристика поля = отношению силы, действующей на зар. со стороны поля,к зар. , т.е.:

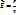q≷0

Напряженность поля численно = силе, действующей на единичный «+» зар. , когда q=+1. Единицы измерения напряжения 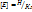или 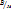, если .

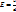Найдем напряжение поля точечного зар. q , находящейся в точке. Хар. вектором в среде, по З.Кулона можем записать

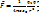
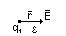
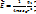- созд. точечный зар.

Если известна Е , то сила со стороны поля действующая на зар. q =:

Сила F, действующая на пробный зар. q в данной точке поля, = векторной сумме сил каждого зар. в отдельности, т.е.:

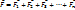, помножим на

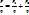… т.е. 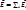- принцип суперпозиции .

Напряженность Эл.п. системы зар. = векторной сумме напряженностей полей, создаваемых каждым зар. в отдельности.

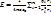
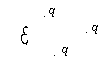
Если непрерывно распределенный зар. т.е.

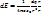
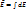
Эл.п. графически изображается с помощью линий напряженности Е, силовых линий, линий Е, метод предложил Фарадей.

Линии напряженности это кривые, касательный к которым в каждой точке совпадают с направлением вектора напряженности в данной точке.

Линии напряженности начинаются на «+» зар. и заканчиваются на «-» или уходят в . Густота силовых линий ,т.е. число линий на ед. площади поверхности перпендикулярной к линиям. Она выбирается так, что количество линий пронизывающих ед. площади поверхности равно или пропорционально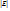

По силовым линиям можно судить о величине и направлении вектора в разных точках пространства. Рассмотрим примеры силовых линий:

Эл.п. называется однородным , если 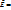const, такое поле реализуется в конденсаторе.