Квантовая механика и физика атома

7.1.1. Определить радиус а₀ первой боровской орбиты и скорость электрона v на ней. Какова напряженность электрического поля ядра на первой орбите?

Ответ: а₀ = 0,53×10^–10 м.

7.1.2. Согласно представлениям классической электродинамики мощность излучения электрона, движущегося с ускорением а равна 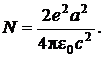Оценить время жизни атома Не⁺, предполагая, что электрон равномерно вращается по круговой орбите с начальным радиусом 10^–10 м.

Ответ: 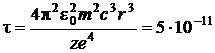с.

7.1.3. Определить частоту света, излучаемого водородоподобным ионом при переходе электрона на уровень с главным квантовым числом n, если радиус орбиты изменился в k раз.

Ответ: 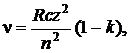где R – постоянная Ридберга.

7.1.4. Фотон с энергией 15,0 эВ выбивает электрон из покоящего атома водорода, находящегося в основном состоянии. С какой скоростью v движется электрон вдали от ядра?

Ответ: v = 7×10⁵ м/с.

7.1.5. Какую скорость v приобретает первоначально покоившийся атом водорода при испускании фотона, соответствующего головной линии серии: а) Лаймана; б) Бальмера?

Ответ: а) 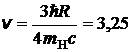м/с; б) 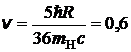м/с.

7.1.6. Определить скорость v, приобретаемую первоначально покоившимся свободным атомом ртути при поглощении им фотона резонансной частоты (резонансной называется частота, отвечающая переходу атома на первый возбужденный уровень). Первый потенциал возбуждения атомов ртути равен 4,9 В.

Ответ: 0,79 см/с.

7.1.7. Свободный покоящийся атом лития поглотил фотон частотой w = 2,81×10¹⁵ с^–1, в результате чего перешел на первый возбужденный уровень и начал двигаться с некоторой скоростью. Затем атом вернулся в основное состояние, испустив новый фотон в направлении, перпендикулярном направлению своего движения. С какой скоростью v движется после этого атом?

Ответ: 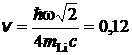м/с.

7.1.8. Определить скорость v₁, с которой электрон движется по первой боровской орбите в атоме водорода.

Ответ: 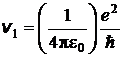= 2,2×10⁶ м/с.

7.1.9. Используя постоянную Планка, массу m_e и заряд е электрона, составить выражение для величины, имеющей размерность длины. Что это за величина?

Ответ: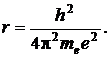

7.1.10. Используя постоянную Планка, массу m_e и заряд е электрона, составить выражение для величины, имеющей размерность энергии. Что это за величина?

Ответ: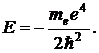

7.1.11. Определить магнитный момент m₁ электрона, находящегося в атоме водорода, на первой боровской орбите. Сравните полученный результат с магнетоном Бора m_Б.

Ответ: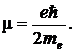

7.1.12. Найти для электрона, находящегося в атоме водорода на n-й боровской орбите, отношение магнитного момента m_n к механическому моменту М_n.

Ответ: е / 2m_e.

7.1.13. Основываясь на том, что потенциал ионизации водородного атома равен 13,6 В, определить длину волны l₁ первой линии а) Лаймана; б) Бальмера; в) Пашена.

Ответ: а) 122 нм; б) 657 нм; в) 1876 нм.

7.1.14. Исходя из того, что первый потенциал возбуждения водородного атома j₁ = 10,2 В, найти длину волны: а) линии Н_a; б) границы серии Бальмера Н_¥.

Ответ: l_a = 660 нм; l_¥ = 370 нм.

7.1.15. Потенциал ионизации водородного атома равен 13,6 В. Исходя из этого, определить, сколько линий серии Бальмера попадает в видимую часть спектра.

Ответ: 4 линии.

7.1.16. Атом водорода находится в основном состоянии. Вычислить: а) вероятность того, что электрон находится внутри области, ограниченной сферой радиусом, равным боровскому радиусу а; б) вероятность того, что электрон находится вне этой области. Волновую функцию считать известной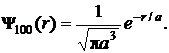

Ответ: w₁ = 0,324; w₂ = 0,674.

7.1.17. Определить: а) потенциал ионизации атома водорода; б) первый потенциал возбуждения атома водорода.

Ответ: а) 13,6 В; б) 10,2 В.

7.1.18. Найти радиусы первых трех боровских орбит атома водорода и скорости электрона на этих орбитах.

Ответ: r₁ = 0,53×10^–10 м; r₂ = 2,12×10^–10 м; r₃ = 4,77×10^–10 м.

7.1.19. Определить длину волны линии спектра испускания атома водорода, излучаемой при переходе электрона с орбиты 4 на орбиту 2.

Ответ: l = 486 нм.

7.1.20. Зная, что нормированная собственная волновая функция, описывающая основное состояние электрона в атоме водорода, имеет вид 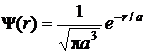, найти среднее расстояние <r> электрона от ядра.

Ответ: 3а / 2.

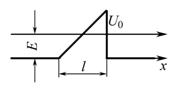
7.1.21. Воспользовавшись формулой для коэффициента прозрачности в случае потенциального барьера произвольной формы, найти для электрона с энергией Е вероятность прохождения потенциального барьера, ширина которого l и высота U₀, если барьер имеет форму, показанную на рисунке.

Ответ: .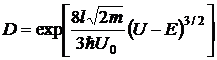

7.1.22. Какой серии принадлежит спектральная линия атомарного водорода, волновое число которой равно разности волновых чисел следующих двух линий серии Бальмера: 486,1; 410,2 нм? Какова длина волны этой линии?

Ответ: l = 2,63×10^-6 м.

7.1.23. Определить коэффициент пропускания прямоугольного потенциального барьера высотой U₀ = 10 эВ и шириной d = 5×10^–10 м для электронов с энергией Е = 9 эВ.

Ответ: t = 5,9×10^–3.

7.1.24. Найти: а) наименьшую и наибольшую длины волн спектральных линий водорода в видимой области спектра (серия Бальмера); б) наименьшую и наибольшую длины волн спектральных линий водорода в ультрафиолетовой области спектра (серия Лаймана); в) наименьшую и наибольшую длины волн спектральных линий водорода серии Пашена в инфракрасной области спектра.

Ответ: а) l_min = 365 нм; l_max = 656 нм;

б) l_min = 910 нм; l_max = 1220 нм;

в) l_min = 821 нм; l_max = 1876 нм.

7.1.25. Электрон находится в потенциальной яме шириной l = 0,5 нм. Определить наименьшую разность DЕ энергетических уровней электрона (в электрон-вольтах). Яма с бесконечно высокими стенками.

Ответ: DЕ = 4,5 эВ.

7.2.1. Волновая функция 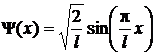описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l. Вычислить вероятность w нахождения частицы в малом интервале Dl = 0,01l в двух случаях: 1) вблизи стенки (0 £ х £ l); 2) в средней части ящика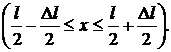

Ответ: w₁ = 6,6×10^–6; w₂ = 0,02.

7.2.2. Кинетическая энергия К электрона в атоме водорода составляет величину порядка 12 эВ. Используя соотношение неопределенностей, оценить минимальные размеры атома l_min.

Ответ: l_min = 113 пм.

7.2.3. Электрон находится в одномерном с бесконечными стенками прямоугольном потенциальном ящике шириной l. Вычислить вероятность w того, что электрон, находящийся в возбужденном состоянии (n = 2), будет находиться в средней третьей части ящика.

Ответ: w = 0,195.

7.2.4. Электрон в потенциальном ящике шириной l характеризуется волновым числом k = pn / 2, где n = 1, 2, 3 … Используя связь энергии Е с волновым вектором k, получить формулу для собственных значений энергии E_n.

Ответ: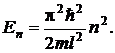

7.2.5. Частица находится в возбужденном состоянии (n = 2) в одномерном прямоугольном потенциальном ящике шириной l с бесконечно высокими стенками. Определить вероятность w обнаружения частицы в области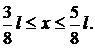

Ответ: w = 0,09.

7.2.6. Электрон находится в возбужденном состоянии (n = 3) в одномерном потенциальном ящике шириной l с бесконечно высокими стенками. Определить вероятность w обнаружения электрона в средней третьей части ящика.

Ответ: w = 0,33.

7.2.7. Определите, во сколько раз применяется отношение разности соседних энергетических уровней частицы Е_n+1, _n / E_n при переходе от n = 3 к n’ = 7.

Ответ: В 2,5 раза.

7.2.8. Электрон с энергией Е = 5 эВ движется в положительном направлении оси х и встречает потенциальный прямоугольный барьер шириной l = 0,1 нм и высотой U = 10 эВ. Определить коэффициент прозрачности D барьера.

Ответ: D = 0,1.

7.2.9. Вероятность прохождения электроном прямоугольного потенциального барьера шириной l = 0,1 нм равна 0,5. Определить высоту барьера U, если кинетическая энергия электрона 2,0 эВ.

Ответ: U = 2,45 эВ.

7.2.10. Определить высоту барьера U прямоугольного потенциального барьера шириной l = 0,1 нм, если коэффициент отражения электрона, имеющего энергию 3,1 эВ, равен 0,5.

Ответ: U = 3,55 эВ.

7.2.11. Электрон с энергией Е движется в положительном направлении оси х и встречает на своем пути бесконечно длинный широкий прямоугольный потенциальный барьер высотой U такой, что E < U. Запишите уравнение Шредингера для электрона внутри барьера и вне его.

7.2.12. Частица с энергией Е = 50 В движется в положительном направлении оси х и встречает на своем пути бесконечно широкий прямоугольный барьер высотой U = 20 эВ. Определить коэффициент отражения R частицы от барьера.

Ответ: R = 0,016.

7.2.13. Электрон с длиной волны де Бройля l₁ = 180 пм движется в положительном направлении оси х и сталкивается с барьером высотой U = 100 эВ. Определить длину волны l₂ де Бройля после прохождения барьера.

Ответ: l₂ = 172 пм.

7.2.14. Частица в потенциальном ящике шириной l находится в возбужденном состоянии (n = 2). Определить, в каких точках ямы (0 < x < l) плотность вероятностей нахождения частицы имеет максимальное и минимальное значения.

Ответ: max (x₁ = l/4; x₃ = 3l/4); min (x₂ = l/2).

7.2.15. Электрон с энергией Е = 25 эВ встречает на своем пути потенциальный барьер с высотой U = 97 В. Определить коэффициент преломления n волн де Бройля на границе барьера.

Ответ: n = 0,8.

7.2.16. Электрон с энергией Е = 100 эВ попадает на потенциальный барьер высотой U = 64 эВ. Определить коэффициент отражения электрона от барьера.

Ответ: R = 0,0625.

7.2.17. Коэффициент отражения протона R от потенциального барьера равен 2,5×10^–5. Найти отношение высоты барьера к кинетической энергии протона. Ответ выразить в процентах.

Ответ: 2 %.

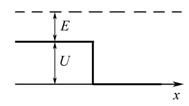
7.2.18. Определить коэффициент преломления волн де Бройля для протонов на границе потенциального барьера (см. рисунок), если кинетическая энергия протонов Е = 16 эВ, высота барьера U = 9 эВ.

Ответ: n = 1,25.

7.2.19. Коэффициент прохождения протонов через потенциальный барьер t = 0,8. Определить показатель преломления волн де Бройля протонов на границе барьера.

Ответ: n₁ = 0,384; n₂ = 2,61.

7.2.20. Атом водорода находится в состоянии 1s. Определить вероятность пребывания электрона в атоме внутри сферы радиусом r = 0,1а, где а – радиус первой боровской орбиты.

Ответ: w = 0,00113.

7.2.21. Электрон в возбужденном атоме водорода находится в 3р-состоянии. Определить изменение магнитного момента, обусловленного орбитальным движением электрона при переходе в основное состояние.

Ответ: Dp_m = –1,31×10^–23 Дж/Т.

7.2.22. На грань кристалла никеля падает параллельный пучок электронов. Кристалл поворачивают так, что угол скольжения изменяется. При угле скольжения равном 64° наблюдается максимум отражения электронов, соответствующее дифракционному максимуму (m = 1). Расстояние между атомными плоскостями d = 2 Å. Определить длину волны де Бройля и их скорость.

Ответ: l = 3,6 Å; v = 2 мм/с.

7.2.23. На грань некоторого кристалла падает под углом 60° к поверхности грани параллельный пучок электронов, движущихся с одинаковой скоростью. Определить скорость электронов, если они испытывают интерференционное отражение первого порядка. Расстояние между гранями кристалла равно 2 Å.

Ответ: v = 2,1 мм/с.

7.2.24. Определить дебройлеровскую длину электрона, находящегося в атоме водорода в основном состоянии.

Ответ: l = 33 нм.

7.2.25. Определите среднюю потенциальную энергию электрона в поле ядра протона, если нормированная волновая функция для 1s-состояния имеет вид 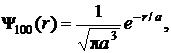где а – первый боровский радиус.

Ответ: