Вынужденные электромагнитные колебания. переменный ток. индуктивность и емкость в цепи переменного тока. мощность переменного тока. трансформатор

Вынужденными колебаниями называют такие колебания, которые вызываются действием на систему внешних сил, периодически изменяющихся с течением времени. В случае электромагнитных колебаний такой внешней силой является периодически изменяющаяся э.д.с. источника тока.

Отличительные особенности вынужденных колебаний: вынужденные колебания - незатухающие колебания; частота вынужденных колебаний равна частоте внешнего периодического воздействия на колебательную систему, т.е., в данном случае, равна частоте изменения э.д.с. источника тока.

Амплитуда вынужденных колебаний зависит от частоты изменения э.д.с. источника тока. Для вынужденных колебаний характерно явление электрического резонанса, при котором амплитуда вынужденных колебаний становится максимальной. Это физическое явление наблюдается при совпадении частоты изменения э.д.с. источника тока с собственной частотой колебаний данного контура, т.е.:

, (1)

где: i - мгновенное значение тока, т.е. его значение в момент времени t = 0;

J₀ - амплитудное или максимальное значение силы тока;

 - частота изменения тока, численно равная частоте изменения э.д.с. источника тока.

Мгновенным или амплитудным значениями тока и напряжения на практике пользоваться неудобно. Амперметры и вольтметры в цепи переменного тока измеряют так называемые действующие или эффективные значения переменного тока, которые связаны с амплитудными значениями тока по формулам:

, (4)

. (5)

Действующими значениями силы тока и напряжения переменного тока называют значения этих величин для такого постоянного тока, который на том же активном сопротивлении выделяет за время, равное периоду Т переменного тока, такое же количество теплоты, как и данный переменный ток.

Источником переменного тока является генератор переменного тока, физический принцип действия которого основан на равномерном вращении с угловой скоростью  плоской рамки площадью S, состоящей из N витков, в однородном магнитном поле с индукцией В. При этом рамку пронизывает переменный магнитный поток:

, (6)

где: Ф₀ - максимальное значение магнитного потока;

 - угол между нормалью к рамке и вектором магнитной индукции В;

- угловая скорость вращения рамки.

Согласно закону электромагнитной индукции, в рамке будет возбуждаться мгновенное значение э.д.с., изменяющееся по закону:

, (7)

где: e - мгновенное значение э.д.с.;

₀ - амплитудное значение э.д.с.;

 - угловая скорость вращения рамки.

В общем случае цепь переменного тока представляет собой колебательный контур:

Напряжение на зажимах источника тока U меняется по гармоническому закону с частотой изменения э.д.с. генератора переменного тока.

Существует принципиальное отличие электрического сопротивления цепи переменного тока по сравнению с электрическим сопротивлением цепи постоянного тока, связанное с преобразованиями электрической энергии в другие виды энергии.

Устройства, в которых электрическая энергия полностью и необратимо преобразуется в другие виды энергии, называют активными нагрузками, а электрические сопротивления этих устройств - активными сопротивлениями. В цепи постоянного тока существуют только активные нагрузки.

Устройства, в которых не происходит необратимого превращения электрической энергии в другие виды энергии, называют реактивными нагрузками, а их сопротивления - реактивными сопротивлениями. Реактивные сопротивления в цепи переменного тока имеют конденсатор и катушка индуктивности, которые соответственно называют емкостным x_c сопротивлением и индуктивным сопротивлением x_L. При этом конденсатор имеет только реактивное сопротивление, а катушка индуктивности, помимо реактивного сопротивления, обладает еще активным сопротивлением. Реактивные сопротивления вычисляются по формулам:

, (8)

, (9)

где: С - емкость конденсатора;

L - индуктивность катушки;

 - частота изменения э.д.с. источника тока.

Если в цепи переменного тока реактивной нагрузки нет или ее сопротивление пренебрежимо мало по сравнению с активным сопротивлением цепи, то колебания силы тока совпадают по фазе с колебаниями напряжения и происходят с частотой и фазой колебаний э.д.с. источника тока:

, (10)

, (11)

. (12)

Цепь переменного тока, которая не содержит конденсатора и активное сопротивление которой ничтожно мало по сравнению с индуктивным сопротивлением, называется цепью переменного тока с индуктивным сопротивлением. В такой цепи колебания напряжения на катушке опережает колебания силы тока на , т.е.:

, (13)

. (14)

Цепь переменного тока, которая не имеет индуктивного сопротивления и активное сопротивление которой пренебрежимо мало по сравнению с емкостным сопротивлением, называется цепью переменного тока с емкостным сопротивлением. В такой цепи колебания силы тока опережают колебания напряжения на :

, (15)

. (16)

Для амплитудного и действующего значений переменного тока справедлив закон Ома:

, (17)

, (18)

, (19)

где величина R называется полным сопротивлением цепи переменного тока.

Количество теплоты Q, выделяющееся на активном сопротивлении, вычисляется по закону Джоуля-Ленца:

. (20)

Величина преобразованной электрической энергии в другие виды энергии определяется мощностью переменного тока. Так как - сила тока и напряжение - переменные величины, то и мощность в цепи переменного тока является переменной величиной. Поэтому имеет смысл говорить только о мгновенном значении мощности , или о среднем значении мощности за период Т изменения переменного тока, вычисляемой по формуле:

. (21)

Мощность называют активной мощностью. Множитель называют коэффициентом мощности, где:  - сдвиг по фазе между колебаниями силы тока и напряжения. Коэффициент мощности вычисляется по формуле:

. (22)

Для преобразования переменного тока одонго напряжения в переменный ток другого напряжения при той же частоте используют устройство, называемое трансформатором. Трансформатор представляет собой систему, состоящую из двух обмоток (катушек), связанных одним сердечником. Если первоначально катушка содержит N₁ витков, а вторичная - N₂ витков, то коэффициент трансформации k вычисляется по формуле:

, (23)

где ₁ и ₂ - э.д.с. индукции в первичной и вторичной обмотках.

Если падение напряжения на активном сопротивлении первичной обмотки трансформатора ничтожно мало, то: и . Тогда:

, (24)

где U₁ и U₂ - напряжение на первичной и вторичной обмотках трансформатора.

К.п.д. трансформатора называют отношение мощности Р₂, отдаваемой вторичной обмоткой, к мощности Р₁, подводимой к первичной обмотке:

. (25)

К.п.д. современных трансформаторов очень высок - 97-98 %. Поэтому по закону сохранения энергии мощность тока в первичной обмотке практически равна мощности тока во вторичной обмотке: Р₁ Р₂. Отсюда следует, что: J₁U₁ J₂U₂.

Тогда формулу (24) можно записать в виде:

, (26)

где: J₁, J₀₁ - действующее и амплитудное значения тока в первичной обмотке;

J₂, J₀₂ -действующее и амплитудное значения тока во вторичной обмотке.

Методические указания к решению задач

Среди задач на вынужденные электромагнитные колебания можно выделить следующие пять групп задач: задачи на вращение плоской рамки в однородном магнитном поле и получение переменной э.д.с.; задачи, требующие знание общих уравнений гармонических колебаний, э.д.с., силы тока и напряжения в цепи; задачи на расчет элементов цепи переменного тока с использованием закона Ома; задачи на тепловое действие переменного тока и расчет мощности тока; задачи о трансформаторах.

Для решения первого из перечисленных типов задач используются формулы (6), (7). При затруднении применения этих формул надо повторить закон электромагнитной индукции, а также основные характеристики вращательного и колебательного движений, связь между ними.

Задачи на составление общих уравнений гармонических колебаний э.д.с., силы тока или напряжения в цепи переменного тока требует не только хорошего знания уравнений (2), (3), (10) - (16), но и четкого понимания того, что такое мгновенное, амплитудное и действующее (эффективное) значения э.д.с., силы тока и напряжения и какая существует связь между амплитудными и действующими значениями этих физических величин (4), (5).

Часто встречается и обратная задача - по заданным уравнениям путем сравнительного анализа с вышеназванными уравнениями определить амплитудное значение колеблющейся величины, фазу между колебаниями силы тока и напряжения, который можно вычислить, через тригонометрические функции, например, по формуле (22).

Большое количество задач связано с расчетом цепи переменного тока с помощью закона Ома. Они похожи на расчет цепи постоянного тока. Трудность лишь в том, что надо внимательно оценивать нагрузку цепи переменного тока в отношении ее сопротивления. В частных случаях, когда в цепи надо учитывать только активное, емкостное или индуктивное сопротивления, задачи решаются довольно просто с учетом формул (8), (9). В общем случае надо использовать закон Ома в виде (17), (18) с учетом полного сопротивления цепи (19).

Задачи на расчет цепи переменного тока предполагают также знание явления электрического резонанса и умения рассчитывать резонансную частоту (1).

Количество теплоты, выделяемое в цепи переменного тока, рассчитывается по закону Джоуля-Ленца (20). Надо быть особенно внимательным при расчете мощности, выделяемой на активной нагрузке цепи переменного тока, которая в общем случае вычисляется с учетом сдвига по фазе между колебаниями силы тока и напряжения (21).

Распространены также задачи технического содержания, в частности, связанные с трансформаторами. Для успешного решения подобных задач надо повторить устройство и принцип действия трансформатора. Расчеты в таких задачах, в основном, связаны со знанием коэффициента трансформации (24), (26) и умения вычислять к.п.д. трансформатора (25).

Примеры решения задач

Задача 1. Определить амплитудное и действующее значения переменной э.д.с., возникающей в рамке при ее вращении с постоянной скоростью в однородном магнитном поле, если при угле поворота рамки на 45 град. мгновенное значение э.д.с. равно 156 В.

Дано:

 = 45 град;

e = 156 В

Найти:

₀ - ? _д - ?

Мгновенное значение э.д.с., возникающей в рамке при равномерном вращении в однородном магнитном поле, прямо пропорционально минусу угла поворота плоскости рамки относительно направления линий индукции магнитного поля, т.е., согласно формуле (7) имеем:

.

Отсюда: ; .

Учитывая связь между амплитудными и действующими значениями физических величин (4), (5), получим:

.

Задача 2. Магнитный поток в рамке, состоящей из 1000 витков и равномерно вращающейся в однородном магнитном поле, изменяется по закону . Найти зависимость мгновенной э.д.с. индукции, возникающей в рамке, от времени. Определить амплитудное и действующее значения э.д.с., период и частоту тока.

N = 1000

Найти:

e(t),₀,_д,T,- ?

Мгновенное значение э.д.с., возникающей в каждом витке e₁ равно первой производной от магнитного потока по времени, взятой со знаком минус. Следовательно: ; .

Учитывая тот факт, что имеется не один виток, а N витком получим:

; .

Анализируя полученное выражение и сравнивая его с формулой (7), получим: .

Соответственно, действующее значение э.д.с.:

.

Для нахождения периода Т и частоты  надо учесть связь между круговой частотой  и периодом Т: и связь круговой частоты  с линейной частотой : .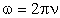

Окончательно получим:

; ; ; .

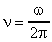Задача 3. В сеть переменного тока с действующим напряжением 220 В и частотой 50 Гц включен контур, состоящий из резистора сопротивлением 100 Ом, конденсатора емкостью 35,4 мкФ и катушки с индуктивностью 0,7 Гн. Написать уравнения U(t) и i(t) зависимости напряжения и силы тока от времени.

Дано:

U_д = 220 В

 = 50 Гц

R_a = 100 Ом

С = 35,4 мкФ

L = 0,7 Гн

Найти:

i(t) - u(t) -

Чтобы успешно справиться с этой задачей, надо помнить, что в цепи переменного тока колебания силы тока и напряжения происходят по синусоидальному закону с одинаковой круговой частотой , но со сдвигом по фазе  (2), (3):

; .

Амплитудное значение напряжения U₀ и круговая частота  легко находятся из данных условия задачи. Действительно: ; ; ; .

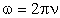Для определения амплитудного значения силы тока J₀ надо воспользоваться законом Ома с учетом формул (19, 4):

; .

Сдвиг фаз между колебаниями силы тока и внешнего напряжения определяется соотношением (22):

; ; .

С учетом полученных числовых значений J₀, U₀, ,  уравнения зависимости силы тока i и напряжения U от времени t получим:

; .

Следовательно, в данной цепи напряжение опережает по фазе силу тока на 0,3  рад, или на 54 град.

Задача 4. Найти падение напряжения на резисторе, конденсаторе и катушке, а также определить частоту переменного тока, при которой в цепи наступит резонанс, воспользовавшись данными предыдущей задачи.

Дано:

U_д = 220 В

R_a = 100 Ом

С = 35,4 мкФ

L = 0,7 Гн

Найти:

U_R,U_C,U_L,₀-

Расчет падения напряжения на различных элементах цепи переменного тока принципиально ничем не отличается от подобного расчета в цепи постоянного тока. Так как элементы цепи соединены последовательно, то:

; ; ; ,

где: .

Окончательно получим:

; ; ; ; ; .

Для нахождения резонансной частоты воспользуемся формулой (1) и формулой :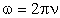

; .

Откуда: ; .

Задача 5. Конденсатор емкостью 0,5 мкФ включен в сеть переменного тока. Определить период колебаний переменного тока, если емкостное сопротивление конденсатора равно 20 Ом.

Дано:

С = 510^-5 Ф

Х_С = 20 Ом

Найти:

Т -

Из формулы емкостного сопротивления (8) с учетом 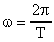выразим Т: .

Откуда: ; .

Задача 6. Катушка индуктивностью 15 мГн включена в сеть промышленного переменного тока. Определить ее индуктивное сопротивление.

Дано:

L=1,510^-2Гн

 = 50 Гц

Найти:

Х_L - ?

В данной задаче надо помнить о том, что частота промышленного тока 50 Гц.

Далее по формуле (9) с учетом - 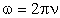находим:

; ;

Задача 7. При включении конденсатора сила тока в цепи переменного тока с частотой 50 Гц и напряжением 220 В равна 0,14 А. Определите емкость конденсатора. Активным сопротивлением цепи можно пренебречь.

Дано:

 = 50 Гц

U_д = 220 В

J_д = 0,14 А

Найти:

С -

Воспользуемся законом Ома для цепи переменного тока (18): .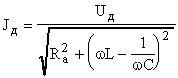

Так как: и индуктивное сопротивление , то закон Ома для цепи с емкостной нагрузкой будет в виде:

.

Отсюда: ; . С учетом соотношения - 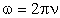перепишем емкостное сопротивление Х_С в виде:

. Откуда: ; .

Задача 8. В сеть переменного тока с частотой 50 Гц и напряжением 220 В включена катушка с индуктивностью 60 мГн и ничтожно малым активным сопротивлением. Найдите действующее и амплитудное значение силы тока в цепи катушки.

Дано:

 = 50 Гц

U_д = 220 В

L = 6010^-3 = = 0,06 Гн

Найти:

J_д, J₀ - ?

Индуктивное сопротивление катушки найдем по формуле (9):

; .

Закон Ома для цепи с индуктивной нагрузкой при и имеет вид: .

Отсюда: .

Амплитудное значение силы тока вычислим по формуле (4):

; .

Задача 9. Конденсатор емкостью 24 мкФ и катушка индуктивностью 0,05 Гн с активным сопротивлением 100 Ом подключены последовательно к источнику переменного тока, в котором напряжение на зажимах равно 120 В при частоте 50 Гц. Определить действующие значения силы тока в цепи напряжения на конденсаторе и катушке.

Дано:

С = 210^-5 Ф

R = 100 Ом

L = 0,05 Гн

 = 50 Гц

U_д = 120 В

Найти:

J_д, U_C, U_L - ?

В данной задаче имеются все элементы цепи переменного тока, поэтому для нахождения силы тока надо воспользоваться законом Ома в общем виде (18) с учетом формулы (19):

.

Учитывая связь - 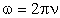, окончательно получаем:

.

Для вычисления действующего напряжения на конденсаторе необходимо силу тока в цепи умножить на емкостное сопротивление конденсатора:

; .

Действующее значение напряжения на катушке равно силе тока, умноженной на полное сопротивление катушки с учетом того, что катушка индуктивности имеет как индуктивное сопротивление, так и активное сопротивление:

; .

Задача № 10. В сеть переменного тока с действующим напряжением 110 В включены последовательно конденсатор с емкостью 510^-5 Ф, катушки индуктивностью 200 мГн и активным сопротивлением 4 Ом. Определить амплитудное значение силы тока в цепи, если частота переменного тока 100 Гц, а также частоту переменного тока, при которой в данном контуре наступит резонанс напряжений.

Дано:

U_д = 110 В

С = 510^-5 Ф

L = 0,2 Гн

R = 4 Ом

 = 100 Гц

Найти:

J₀, _рез - ?

По закону Ома (17) - (19) амплитудное значение силы тока: .

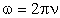С учетом: и окончательно получаем:

; .

При резонансе частота вынужденных колебаний переменного тока совпадает с частотой собственных колебаний контура. Отсюда:

; .

Задача № 11. Электропечь, сопротивление которой 22 Ом, питается от генератора переменного тока. Определить количество теплоты, выделяемое печью за 1 час, если амплитудное значение силы тока 10 А.

Дано:

R = 22 Ом

t = 3,610⁴ с

J₀ = 10 А

Найти:

Q - ?

Количество теплоты, выделяемое в цепи переменного тока на активном сопротивлении, можно вычислять по закону Джоуля-Ленца, используя действующие значения силы тока или напряжения. В данном случае: .

Учитывая связь - , окончательно получаем: ; ; .

Задача 12. На входе линии электропередачи, потребляющей мощности 100 кВт, подается напряжение 220 В. Определить потери мощности в проводах, сопротивление которых 0,01 Ом при сдвиге фазы 37 град. между колебаниями силы тока и напряжения.

Дано:

P = 10⁵ B

U_д = 220 В

R = 0,01 Ом

 = 37 град

Найти:

Р₁ - ?

Мощность, потребляемая активным сопротивлением, как и в случае постоянного тока, вычисляется по формуле:

.

Действующее значение силы тока может быть вычислено по формуле (2): , откуда: .

Окончательно получаем: ; .

Задача 13. Трансформатор имеет коэффициент трансформации 18. Напряжение на первичной обмотке, содержащей 450 витков, равно 220 В. Определите напряжение на вторичной обмотке и число витков в ней.

Дано:

k = 18

N₁ = 450

U₁ = 220 B

Найти:

U₂, N₂ - ?

Решение:

Воспользуемся формулой для коэффициента трансформации (24):

.

Откуда:

; ; ; .

Задача 14. Сила тока в первичной обмотке трансформатора J₁ = 15000 А и напряжение на ее зажимах U₁ = 11000 В. Сила тока во вторичной обмотке J₂ = 1500 А. Определить напряжение на зажимах вторичной обмотки трансформатора, если к.п.д. равен 96 %.

Дано:

J₁ = 15000 A

U₁ = 11000 B

J₂ = 1500 A

к.п.д. = 0,96

Найти:

U₂ - ?

Коэффициент полезного действия трансформатора по определению вычисляется по формуле (25):

К.п.д. = ,

где: ; .

Отсюда к.п.д. = .

Окончательно получаем:

; .

Задача 15. Первичная обмотка трансформатора имеет 500 витков, вторичная - 50 витков. В первичной обмотке сила тока изменяется по закону: . По какому закону изменяется сила тока во вторичной обмотке в рабочем режиме трансформатора Считать, что токи в первичной и вторичной обмотках совершают колебания в одинаковых фазах.

Дано:

N₁ = 500

N₂ = 50

Найти:

i₂(t) - ?

Так как колебания тока в обмотках совершаются в одинаковых фазах, то законы изменения силы тока будут отличаться только амплитудными значениями силы тока.

Для того, чтобы найти амплитудное значение тока во вторичной обмотке трансформатора, надо воспользоваться выражениями для коэффициента трансформации (24), (26):

.

Отсюда получим: ; .

Теперь можно записать закон изменения силы тока во вторичной обмотке: .

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

Краткая теория

Электромагнитные волны - электромагнитные колебания, распространяющиеся в пространстве с течением времени. Источником электромагнитных волн является открытый колебательный контур.

В электромагнитной волне происходят колебания напряженности электрического поля и индукции магнитного поля. Вектора и перпендикулярны друг другу и направлению распространения волны, т.е. электромагнитные волны - поперечные волны.

Основной характеристикой электромагнитной волны является ее скорость, величина которой зависит от свойств среды, в которой волна распространяется. В вакууме скорость электромагнитных волн равна скорости света - 310⁸ м/с. Следующей важной характеристикой волны является длина волны - . Длина волны - это расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, с другой стороны, - это расстояние, на которое перемещается волна с заданной скоростью v за время t, равное периоду колебаний T:

. (1)

Учитывая связь между периодом Т и частотой колебаний - , формулу (1) можно переписать в виде:

. (2)

В вакууме: . (3)

С помощью электромагнитных волн осуществляется радиосвязь, радиовещание, радиолокация, космическая связь и т.д.

Методические указания к решению задач

Решение задач в школьном курсе физики сводится, в основном, к двум типам. В первую очередь, это расчет длины волны, излучаемой колебательным контуром, через частоту собственных колебаний в данном контуре.

Для вычисления собственной частоты колебаний применяется формула:

. (4)

Для вычисления периода собственных колебаний применяют формулу .Томсона: 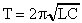. (5)

Если излучение происходит в воздухе, то скорость электромагнитных волн можно считать равной скорости эл. м. волн в вакууме - с. Если о среде нет никаких дополнительных сведений, то в большинстве случаев подразумевается вакуум и в качестве скорости берется та же скорость - с.

Возможна и обратная задача - по известной излучаемой длине волны требуется вычислить какой-нибудь из параметров колебательного контура.

Приемником электромагнитных волн также является колебательный контур, резонирующий на определенную длину волны. Поэтому при решении задач на прием электромагнитных волн необходимо помнить о явлении электрического резонанса и условии, при котором это явление наблюдается:

. (6)

Второй тип задач связан, в основном, с применением электромагнитных волн, например, в радиолокации. Надо помнить, что в этом случае пользуются одним из свойств электромагнитных волн - отражением электромагнитных волн от границы раздела двух различных сред.

Примеры решения задач

Задача 1.Определить длину электромагнитных волн в воздухе, излучаемых колебательным контуром с емкостью 3 нФ и индуктивностью 0,012 Гн. Активное сопротивление контура принять равным нулю.

Дано:

С = 310^-9 Ф

L = 0,012 Гн

R_a = 0

v=c= 310⁸м/с

Найти:

 - ?

Решение:

Согласно определению длина волны определяется по формуле (1): .

Подставляя значение для периода собственных колебаний (5) в формулу (1), получим:

;

.

Задача 2. Колебательный контур излучает в воздухе электромагнитные волны длиной 300 м. Определить индуктивность колебательного контура, если его емкость равна 5 мкФ. Активное сопротивление контура не учитывать.

Дано:

l = 300 м

С = 510^-6 Ф

R_a = 0

С = 310⁸ м/с

Найти:

L - ?

Решение:

Решая совместно два уравнения (1) и (5), получаем:

и .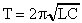

Отсюда получим:

; ; ;

.

Задача 3. На какую длину волны будет резонировать колебательный контур, в котором индуктивность катушки 8 мкГн, а емкость конденсатора 20 нФ

Дано:

L = 810^-6 Гн

С = 210^-8 Ф

с = 310⁸ м/с

Найти:

_рез - ?

Решение:

Электрический резонанс наступает в контуре при условии, если частота колебаний электрического поля и магнитного поля в электромагнитной волне совпадает с частотой электромагнитных колебаний в контуре, т.е. по формуле (6) имеем:

.

Тогда длина волны легко рассчитывается по формуле (3):

,

.

Задача 4. Радиопередатчик работает на частоте 6 МГц. Сколько волн укладывается на расстоянии 100 км по направлению распространения радиосигнала

Дано:

 = 610⁶ Гц

S = 10⁵ м

c = 310⁸ м/с

Найти:

n - ?

Решение:

На данном расстоянии очевидно должно укладываться целое число длин волн, т.е.: .

Так как длина волны вычисляется по формуле (3), то окончательно получим: ; .

Задача 5. Радиолокатор работает в импульсном режиме. Частота повторения импульсов 1700 Гц, длительность импульса 0,8 мкс. Найти максимальную и минимальную дальность обнаружения цели данным локатором.

Дано:

f = 1700 Гц

 = 0,8 мкс =

= 810^-7 с

с = 310⁸ м/с

Найти:

l, L - ?

Решение:

Для того, чтобы по положению отраженного импульса на экране радиолокатора можно было судить о расстоянии до цели, необходимо, чтобы отраженный импульс пришел не ранее, чем через время , и не позднее, чем через время , после начала посылки прямого импульса.

Следовательно, минимальное расстояние до цели:

; ,

где:  - время возвращения сигнала после отражения от цели, учитывая, что сигнал проходит расстояние l дважды.

Максимальное расстояние до цели:

; .