Вопрос 16. Стационарное уравнение Шрёдингера

Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда 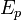не является функцией времени, можно записать в виде:

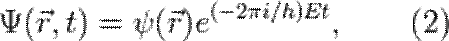
где функция 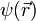должна удовлетворять уравнению:

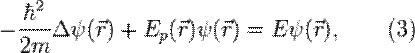
которое получается из уравнения Шрёдингера (1) при подстановке в него указанной выше формулы для 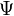(2). Заметим, что это уравнение вообще не содержит времени; в связи с этим оно называется стационарным уравнением Шрёдингера (уравнение Шрёдингера, не содержащее времени).

Выражение (2) является лишь частным решением зависящего от времени уравнения Шрёдингера (1), общее решение представляет собой линейную комбинацию всех частных решений вида (2). Зависимость функции 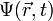от времени проста, но зависимость её от координаты не всегда имеет элементарный вид, так как уравнение (3) при одном выборе вида потенциальной функции 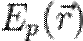совершенно отличается от того же уравнения при другом выборе этой функции. В действительности, уравнение (3) может быть решено аналитически лишь для небольшого числа частных типов функции .

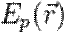Важное значение имеет интерпретация величины 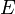в уравнении (2). Она производится следующим путём: временна́я зависимость функции 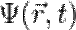в уравнении (2) имеет экспоненциальный характер, причём коэффициент при 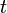в показателе экспоненты выбран так, что правая часть уравнения (3) содержит просто постоянный множитель 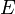. В левой же части уравнения (3) функция 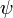умножается на потенциальную энергию 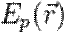. Следовательно, из соображений размерности вытекает, что величина 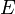должна иметь размерность энергии. Единственной величиной с размерностью энергии, которая постоянна в механике, является полная (сохраняющаяся) энергия системы; таким образом, можно предполагать, что 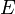представляет собой полную энергию. Согласно физической интерпретации уравнения Шрёдингера, 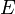действительно является полной энергией частицы при движении, описываемом функцией .

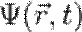квантование энергии является одним из ключевых принципов, необходимых для понимания структурной организации материи, т.е. существования стабильных, повторяющихся в своих свойствах, молекул, атомов и более мелких структурных единиц, из которых состоит как вещество, так и излучение.

Принцип квантования энергии гласит, что любая система взаимодействующих частиц, способная образовывать стабильное состояние — будь то кусок твердого тела, молекула, атом или атомное ядро, — может сделать это только при определенных значениях энергии. Уровни энергии любой такой системы состоят из уровня основного состояния , соответствующего минимальному возможному значению энергии, и (бесконечного) набора дискретных уровней Система может находиться в состояниях только с этими определенными уровнями энергии, причем основное состояние всегда является наиболее вероятным, т.е. стабильная система проводит большую часть времени в основном состоянии. Кроме того, всегда существует предельное значение энергии, выше которого начинается так называемый сплошной спектр энергии. При энергия не квантуется, т.е. система может находиться в состоянии с любым значением энергии, большим .

Опера́тор на́бла (оператор Гамильтона) — векторный дифференциальный оператор, обозначаемый символом (набла) (в Юникоде U+2207, ∇). Для трёхмерного евклидова пространства в прямоугольных декартовых координатах^[1] оператор набла определяется следующим образом:

,

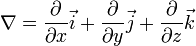где 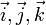— единичные векторы по осям x, y, z.

Через оператор набла естественным способом выражаются основные операции векторного анализа: grad (градиент), div (дивергенция), rot (ротор), а также оператор Лапласа (см. ниже). Широко употребляется в описанном смысле в физике и математике (хотя иногда графический символ используется также для обозначения некоторых других, хотя в некотором отношении не совсем далеких от рассмотренного, математических объектов, например, ковариантной производной).

Под n-мерным оператором набла подразумевается вектор с компонентами 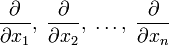в n-мерном пространстве^[2].

Иногда, особенно при начертании от руки, над оператором набла рисуют стрелку: — чтобы подчеркнуть векторный характер оператора. Смысл такого начертания ничем не отличается от обычного .

§ Иногда (особенно когда речь идет только о применении к скалярным функциям), оператор набла называют оператором градиента, каковым он в применении к скалярным функциям (полям) и является.

§ Замечание: в физике в наше время название оператор Гамильтона по отношению к оператору набла стараются не употреблять, особенно в квантовой физике, во избежание путаницы с квантовым гамильтонианом, имеющим, в отличие от классического, операторную природу.