Вычисление разности потенциалов по

Напряженности поля

Установленная в § 85 связь между напряженностью поля и потенциалом позволяет по известной напряженности поля найти разность потенциалов между двумя произвольными точками этого поля.

1. Поле равномерно заряженной бесконечной плоскости определяется формулой (82.1):

где s — поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях х₁ и х₂от плоскости, равна (используем формулу (85.1))

2. Поле двух бесконечных параллельных разноименно заряженных плоскостей определяется формулой (8X2): Е = s/e₀, где s — поверхностная плотность заряда. Разность потенциалов между плоскостями, расстояние между которыми равно d (см. формулу (85.1)), равна

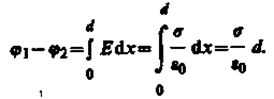(86.1)

3. Поле равномерно заряженной сферической поверхности радиуса Rс общим зарядом Qвнесферы (r > R) вычисляется по (82.3): 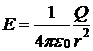. Разность потенциалов между двумя точками, лежащими на расстояниях r₁ и г₂ от центра сферы (r₁ > R, r₂ > К, r₂ > r₁), равна

(86.2)

Если принять r₁ = r и r₂ = ¥, то потенциал поля вне сферической поверхности, согласно формуле (86.2), задается выражением

(ср. с формулой (84.5)). Внутри сферической поверхности потенциал всюду одинаков и равен

График зависимости jот rприведен на рис. 134.

Рис. 134

3.Поле объемно заряженного шара радиуса Rс общим зарядом Q внешара (r > R) вычисляется по формуле (82.3), поэтому разность потенциалов между двумя точками, лежащими на расстояниях r₁ и г₂ от центра шара (r₁ > R, г₂ > R, г₂ > г₁),определяется формулой (86.2). В любой точке, лежащей внутри шара на расстоянии r' от его центра (r¢ < R), напряженность определяется выражением (82.4):

Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях r¢₁ и r¢₂ от центра шара (r¢₁ < R, r¢₂ < R, r¢₂ > r¢₁) равна

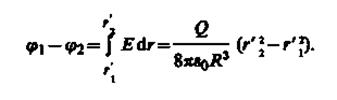
5. Поле равномерно заряженного бесконечного цилиндра радиуса R, заряженного с линейной плотностью t, вне цилиндра (r > R)определяется формулой (82.5): Е= . Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях r₁ и г₂ от оси заряженного цилиндра (r₁ >R. г₂ > R,г₂ > г₁), равна

(86.3)

Типы диэлектриков. Поляризация

Диэлектриков

Диэлектрик (как и всякое вещество) состоит из атомов и молекул. Так как положительный заряд всех ядер молекулы равен суммарному заряду электронов, то молекула в целом электрически нейтральна. Если заменить положительные заряды ядер молекул суммарным зарядом + Q, находящимся в центре «тяжести» положительных зарядов, а заряд всех электронов — суммарным отрицательным зарядом —Q, находящимся в центре «тяжести» отрицательных зарядов, то молекулу можно рассматривать как электрический диполь с электрическим моментом, определяемым формулой (80.3). Первую группу диэлектриков (N₂, Н₂, О₂, СО₂, СН₄, ...) составляют вещества, молекулы которых имеют симметричное строение, т. е. центры «тяжести» положительных и отрицательных зарядов в отсутствие внешнего электрического поля совпадают и, следовательно, дипольный момент молекулы р равен нулю. Молекулы таких диэлектриков называются неполярными. Под действием внешнего электрического поля заряды неполярных молекул смещаются в противоположные стороны (положительные по полю, отрицательные против поля) и молекула приобретает дипольный момент.

Вторую группу диэлектриков (Н₂О, NH₃, SO₂, CO,...) составляют вещества, молекулы которых имеют асимметричное строение, т. е. центры «тяжести» положительных и отрицательных зарядов не совпадают. Таким образом, эти молекулы в отсутствие внешнего электрического поля обладают дипольным моментом. Молекулы таких диэлектриков называются полярными. При отсутствии внешнего поля, однако, дипольные моменты полярных молекул вследствие теплового движения ориентированы в пространстве хаотично и их результирующий момент равен нулю. Если такой диэлектрик поместить во внешнее поле, то силы этого поля будут стремиться повернуть диполи вдоль поля и возникает отличный от нуля результирующий момент.

Третью группу диэлектриков (NaCl, KC1, КВг, ...) составляют вещества, молекулы которых имеют ионное строение. Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В этих кристаллах нельзя выделить отдельные молекулы, а рассматривать их можно как систему двух вдвинутых одна в другую ионных подрешеток. При наложении на ионный кристалл электрического поля происходит некоторая деформация кристаллической решетки или относительное смещение подрешеток, приводящее к возникновению дипольных моментов.

Таким образом, внесение всех трех групп диэлектриков во внешнее электрическое поле приводит к возникновению отличного от нуля результирующего электрического момента диэлектрика, или, иными словами, к поляризации диэлектрика. Поляризацией диэлектрика называется процесс ориентации диполей или появления под воздействием внешнего электрического поля ориентированных по полю диполей.

Соответственно трем группам диэлектриков различают три вида поляризации:

электронная, или деформационная, поляризация диэлектрика с неполярными молекулами, заключающаяся в возникновении у атомов индуцированного дипольного момента за счет деформации электронных орбит;

ориентационная, или дипольная, поляризация диэлектрика с полярными молекулами, заключающаяся в ориентации имеющихся дипольных моментов молекул по полю. Естественно, что тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обоих факторов (электрическое поле и тепловое движение) возникает преимущественная ориентация дипольных моментов молекул по полю. Эта ориентация тем сильнее, чем больше напряженность электрического поля и ниже температура;

ионная поляризация диэлектриков с ионными кристаллическими решетками, заключающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицательных — против поля, приводящем к возникновению дипольных моментов.