Стационарные состояния, их временная зависимость. Уравнение Шредингера для стационарных состояний.
Стационарные состояния – это состояния с фиксированными значениями энергии. Это возможно, если силовое поле, в котором движется частица, стационарно, т.е. функция U=U(x,y,z) не зависит явно от времени и имеет смысл потенциальной энергии. Уравнение Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая - только времени, причем зависимость от времени выражается множителем e-iωt=e-i(E/ħ)t, так что Ψ(x,y,z,t)=ψ(x,y,z)e-i(E/ħ)t, где Е- полная энергия частицы, постоянная в случае стационарного поля. Подставляя это выражение в уравнение Шредингера((–ħ2/2m)ΔΨ+U(x,y,z,t)Ψ=iħ(∂Ψ/∂t), где ħ=h/(2π), m –масса частицы, i-мнимая единица, U-потенциальная функция частицы в силовом поле, в котором она движется
Δ-оператор Лапласа(ΔΨ=∂2Ψ/∂x2+∂2Ψ/∂y2+∂2Ψ/∂z2), Ψ(x,y,z,t)-искомая волновая функция частицы) получим:
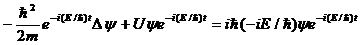разделив на общий множитель e-i(E/ħ)t и преобразовав придем к уравнению, определяющему функцию ψ
Δψ+(2m/ħ2)(E-U)ψ=0-уравнение Шредингера для стационарных состояний. Это уравнение имеет бесчисленное количество решений, из которых посредством наложения граничных условий отбираются решения, имеющие физич.смысл. Условия: волновые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными. Т.о. реальный физич.смысл имеют только такие решения, которые выражаются регулярными функциями ψ .
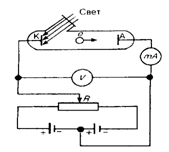
достаточно малой частоте ν=ν0 кинет.энергия фотоэлектронов станет равной 0 и фотоэффект прекратится(3 закон). Получили ν0=A/h- красная граница фотоэффекта для данного металла. Согласно гипотезе световых квантов Эйнштейна, свет испускается, поглощается и распространяется дискретными порциями, названными фотонами. Энергия фотона ε0=hν/c2. Его масса находится из закона взаимосвязи массы и энергии mγ=hν/c2.
Из отношения E=ħω следует,что 1)масса покоя фотона равна0 2)фотон всегда движется со скоростью p=ħ2π/λ=ħk(k-волновое число. р и к направлены в сторону распространения волны.
Свет, обладая одновременно корпускулярными и волновыми свойствами, обнаруживает определенные закономерности в их проявлении. Так, волновые свойства света проявляются в закономерностях его распространения, интерференции, дифракции, поляризации, и корпускулярные - в процессах взаимодействия света с веществом. Чем больше длина волны, тем меньше энергия и импульс фотона и тем труднее обнаруживаются квантовые свойства света( с этим связано существование красной границы фотоэффекта).
Эффект Комптона.
Эффектом Комптона наз.упругое рассеяние коротковолнового электромагнитного излучения на свободных электронах вещества, сопровождающееся увеличением длины волны. Комптон экспериментально доказал Δλ=λ`-λ=2λcsin2(θ/2)( λ`-длина волны рассеянного излучения, λ-длина волны падающего света, λс- комптоновская длина волны( при рассеянии фотона на электроне λс=2,426 пм). Эффект Комптона не может наблюдаться в видимой области спектра, поскольку энергия фотона видимого света сравнима с энергией связи электрона с атомом, при этом даже внешний электрон нельзя считать свободным. Эффект Комптона наблюдается не только на электронах, но и на других заряженных частицах, например на протонах, однако из-за большой массы протона его отдача просматривается лишь при рассеянии фотонов с очень высокой энергией.