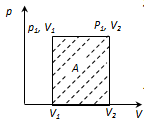
Работа газов при изменении его объема

Рассмотрим газ, находящийся под поршнем и в цилиндре.

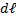Если газ, расширяясь, передвигает поршень на бесконечно малое расстояние , то газ производит над поршнем работу.

где S - площадь поршня.

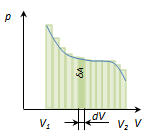Полная работаА, совершаемая газом при изменению объема от V₁ до V₂ равная

• работа для любого процесса

3 С_р, C_V и связь между ними (уравнения Майера)

Запишем выражения I начала термодинамики для 1 моля газа

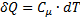
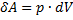
Если газ нагревается при постоянном объеме (V = const, dV = 0), тоА= 0, и, сообщаемая газу теплота, идет только на увеличения его внутренней энергии

то есть молярная теплоемкость газа при постоянном объеме C_V равна изменению внутренней энергии 1 моля газа при повешении температуры на 1К.

Т.к.

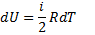
Если газ нагревается при постоянном давление p = const

так как не зависят от вида процесса (внутренняя энергия не зависит от р и V, а определяется лишь температурой Т ) и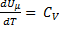

Из уравнения Менделеева-Клапейронаpv=RT

p

- уравнение Майера

Уравнение Майера показывает, что С_р всегда больше C_v на величину универсальной газовой постоянной R,так как при p = const требуется дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличениям объема газа

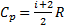
Величина

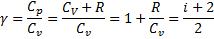
представляет характерную для каждого газа величину. Для одноатомных газов , для двухатомных - 7/5, для трехатомных – 4/3.

I начало термодинамики,

Q, U, A для изопроцессов

• Изотермический процессТ = const, m=const

Закон Бойля-Мариотта

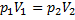=const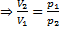

a)A=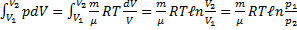

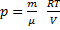
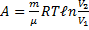
б) 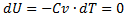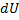=0

в )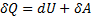

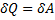
т.е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил

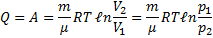
чтобы при работе расширения температура не изменялась, к газу в течение изобарного процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.

• Изобарический процесс. p=const m=const
• A=

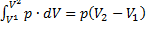
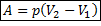
Из уравнения Менделеева-Клапейрона для состояния 1 и 2:

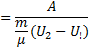
Физический смысл R: R численно равна работе при нагревании 1 моля газа на 1К (T₂ - T₁ = 1 K) при изобарическом процессе.

б)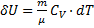

в)

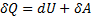
Q=

тепло, подведенное к газу, идет на изменение его внутренней энергии и совершение работы.

3.Изохорический процесс. V = const, m = const.

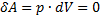
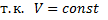
и

,

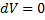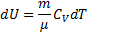
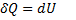
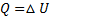
Вся теплота, сообщаемая газу, идет на изменение его внутренней энергии.

Адиабатический процесс.

Политропный процесс

Адиабатическим называется процесс, протекающий без теплообмена с внешней средой. К адиабатическим можно отнести все быстропротекающие процессы. Например, адиабатным процессом можно считать процесс распространения звука в среде, т.к. скорость распространения звука настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатические процессы применяются в двигателях внутреннего сгорания, холодильных установках и др.

Найдем уравнение, связывающее параметры идеального газа при адиабатном процессе.

Запишем I начало термодинамики.

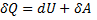
Для адиабатического процесса

т.е. внешняя работа совершается за счет изменения внутренней энергии системы.

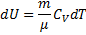
Из уравнения Менделеева-Клапейрона выразим р:

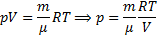
Перепишем в виде:

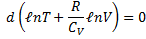
т.е

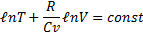
Пропотенцировав

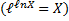
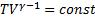
• уравнение адиабаты в координатахТ и V.

Уравнение Пуассона (уравнение адиабаты в координатах р и V):

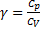-показатель адиабаты (или коэффициент Пуассона).

pV = const - уравнение изотермы, т.к. γ > 1, то адиабата идет круче, чем изотерма. Это объясняется тем, что при адиабатическом сжатии 1-3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры

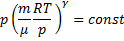
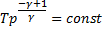
• уравнение адиабаты в координатах p, T.

Вычислим работу совершаемую газом в адиабатическом процессе.

I начало термодинамики для адиабатического процесса

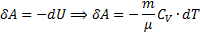
Если газ адиабатически расширяется от объема V₁ до V₂, то его температура уменьшается от Т₁ до Т₂ и работа расширения идеального газа

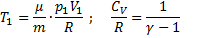
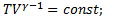
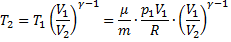
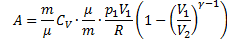
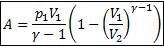
Работа, совершаемая газом при адиабатическом расширении 1-2 равна площади, заштрихованной на рисунке и она меньше, чем работа при изотермическом расширении. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

Рассмотренные изохорический, изобарический, изотермический и адиабатический процессы имеют общую особенность – они протекают при постоянной теплоемкости (C_V, C_P, C_T= ∞ , C_A=0). В первых двух процессах теплоемкости соответственно равны С_v и C_р в изотермическом процессе (dT = 0) С_T = ∞, в адиабатическом процессе δQ = 0 и C_A=0.

Процесс, в котором теплоемкость остается постоянной называется политропным (C = const).

Исходя из I начала термодинамики при условии постоянства теплоемкости (C = const) можно вывести уравнения политропы

n – показатель адиабаты.

ПриС = 0 n = γ pv^γ=const -уравнения адиабаты

ПриС = ∞ n = 1 pV = const – уравнение изотермы

ПриС = С_р n = 0 p = const,

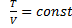-уравнение изобары

ПриС = С_V n = ± ∞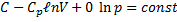

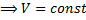
т.о., все рассмотренные процессы являются частными случаями политропного процесса.

Работа газа при адиабатическом процессе

Из первого начала термодинамики ( 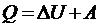) для адиабатического процесса ( 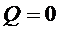) следует, что .

Если газ адиабатически расширяется от объема V₁ до объема V₂ , то его температура уменьшается от T₁ до T₂ и работа расширения идеального газа:

.

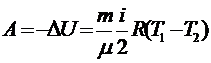Используя уравнение адиабатического процесса в переменных V и Т, то есть 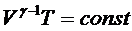полученное выражение для работы А при адиабатическом расширении газа можно преобразовать к иному виду, отражающему адиабатическое изменение объема газа от величины V₁ до величины V₂ :

.

Адиабатный процесс. Изопроцессы в термодинамике

На этом уроке мы будем работать с уже известными нам физическими понятиями, но в несколько иной области применения. А именно с изопроцессами в термодинамике. Мы рассмотрим, какие изменения в первый закон термодинамики (закон сохранения энергии в тепловых процессах) внесут протекания этих самых процессов при неизменном макроскопическом параметре газа. Также мы рассмотрим новый, ранее неизвестный процесс – адиабатный.

В ходе изу­че­ния темы «Ос­но­вы мо­ле­ку­ляр­но-ки­не­ти­че­ской тео­рии» нами были рас­смот­ре­ны так на­зы­ва­е­мые изо­про­цес­сы, то есть про­цес­сы, про­те­ка­ю­щие при неиз­мен­ном одном из мак­ро­ско­пи­че­ских па­ра­мет­ров(дав­ле­нии, объ­ё­ме или тем­пе­ра­ту­ре). При под­ста­нов­ке этих дан­ных в урав­не­ние Кла­пей­ро­на эти усло­вия несколь­ко ви­до­из­ме­ня­ли его. Те­перь же мы про­де­ла­ем схо­жий ана­лиз, но уже с пер­вым за­ко­ном тер­мо­ди­на­ми­ки:

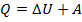
Рас­смот­рим слу­чай про­те­ка­ния про­цес­са при неиз­мен­ной тем­пе­ра­ту­ре:

Так как:

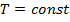
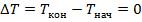
Сле­до­ва­тель­но:

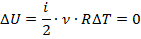
А, зна­чит, пер­вый закон тер­мо­ди­на­ми­ки при­об­ре­та­ет вид:

Рас­смот­рев слу­чай для вы­пол­не­ния над газом внеш­ни­ми си­ла­ми по­ло­жи­тель­ной ра­бо­ты:

То есть, при изо­тер­ми­че­ском сжа­тии или рас­ши­ре­нии газ вы­де­ля­ет теп­ло­ту в окру­жа­ю­щую среду.

Рас­смот­рим слу­чай, когда про­цесс про­те­ка­ет при по­сто­ян­ном дав­ле­нии:

Так как ни в одну тер­мо­ди­на­ми­че­скую ве­ли­чи­ну не вхо­дит мно­жи­тель 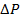, то ни­ка­кое сла­га­е­мое пер­во­го за­ко­на тер­мо­ди­на­ми­ки не об­ну­ля­ет­ся, и он со­хра­ня­ет свой преж­ний вид:

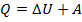
Те­перь рас­смот­рим, какие из­ме­не­ния про­изой­дут в за­пи­си пер­во­го за­ко­на тер­мо­ди­на­ми­ки, если про­цесс про­ис­хо­дит в фик­си­ро­ван­ном объ­ё­ме.

Так как:

Сле­до­ва­тель­но:

А зна­чит, пер­вый закон тер­мо­ди­на­ми­ки при­об­ре­та­ет вид:

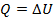
То есть те­ря­ет­ся смысл ис­поль­зо­ва­ния изо­хор­ных про­цес­сов в теп­ло­вых дви­га­те­лях, ведь вся энер­гия сго­ра­е­мо­го топ­ли­ва пой­дёт на из­ме­не­ние внут­рен­ней энер­гии, и газ не будет со­вер­шать по­лез­ной ра­бо­ты.

Су­ще­ству­ет также ещё один очень важ­ный про­цесс – адиа­бат­ный.

Опре­де­ле­ние.Адиа­бат­ный про­цесс – про­цесс, про­те­ка­ю­щий в теп­ло­изо­ли­ро­ван­ной си­сте­ме. То есть без под­во­да газу или вы­де­ле­ния газом теп­ло­ты.

Так как:

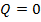
Пер­вый закон тер­мо­ди­на­ми­ки при­об­ре­та­ет вид:

Или

То есть в ре­зуль­та­те вы­пол­не­ния над газом ра­бо­ты внеш­ни­ми си­ла­ми его внут­рен­няя энер­гия, а сле­до­ва­тель­но, и тем­пе­ра­ту­ра уве­ли­чи­ва­ет­ся, а при вы­пол­не­нии ра­бо­ты газом – умень­ша­ет­ся.

На­гляд­ны­ми при­ме­ра­ми по­след­них двух утвер­жде­ний яв­ля­ют­ся сле­ду­ю­щие опыты.

1. В за­кры­том по­движ­ным порш­нем ци­лин­дре на­хо­дит­ся неболь­шое ко­ли­че­ство топ­ли­ва. После быст­ро­го на­жа­тия на пор­шень топ­ли­во вос­пла­ме­ня­ет­ся.

2. В за­кры­том проб­кой с про­де­тым шлан­гом на­со­са со­су­де на­хо­дит­ся неболь­шое ко­ли­че­ство воды. После на­гне­та­ния в сосуд опре­де­лен­но ко­ли­че­ства воз­ду­ха, проб­ка быст­ро вы­ле­та­ет и в со­су­де на­блю­да­ет­ся туман (рис. 1).

Рис. 1. На­гляд­ные при­ме­ры адиа­бат­ных про­цес­сов (Ис­точ­ник)

В двух слу­ча­ях газ вы­пол­ня­ет раз­ные по знаку ра­бо­ты, и, сле­до­ва­тель­но, из­ме­не­ние внут­рен­ней энер­гии и тем­пе­ра­ту­ры имеет раз­ные знаки. В обоих слу­ча­ях де­ла­ет­ся ак­цент на быст­ром из­ме­не­нии объ­ё­ма по­то­му, что невоз­мож­но со­здать иде­аль­но изо­ли­ро­ван­ную си­сте­му, но если рас­смат­ри­вать очень ско­ро­теч­ный про­цесс, то тепло не успе­ет пе­ре­дать­ся, и про­цесс можно счи­тать адиа­бат­ным.

Гра­фик адиа­бат­ных про­цес­сов в ко­ор­ди­на­тах P-V вы­гля­дит сле­ду­ю­щим об­ра­зом (рис. 2).

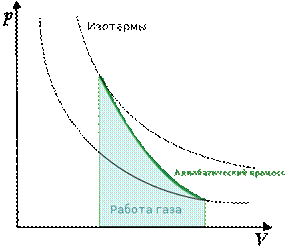
Рис. 2. Гра­фик адиа­бат­но­го про­цес­са (Ис­точ­ник)

На­чи­ная со сле­ду­ю­ще­го урока, мы пе­ре­хо­дим к изу­че­нию но­во­го раз­де­ла фи­зи­ки – элек­тро­ста­ти­ки.