Занятие № 6. Интегрирование тригонометрических функций

Цель занятия - научиться брать интегралы вида 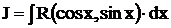, где R- рациональная функция относительно .

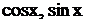Интегралы вида J находили в конце прошлого занятия в примерах 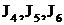где использовались тригонометрические подстановки. Разобранные там примеры были достаточно простые. В общем же случае вопрос решает следующая теорема.

Теорема. Всякий интеграл J с помощью подстановки 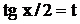приводится к интегралу от рациональной дроби.

Доказательство.Из подстановки следует, что 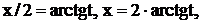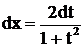. Кроме того, используем известные формулы тригонометрии:

.

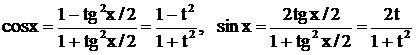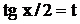После замены их значениями получим интеграл от рациональной дроби относительно t. Подстановка в силу ее всеобщности называется универсальной тригонометрической подстановкой.

Пример. Найти интеграл .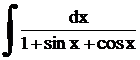

Решение. После замены 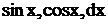их значениями, получим

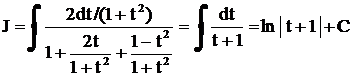, где , .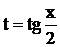

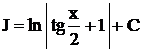Пример. Найти самостоятельно интеграл .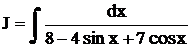

Универсальная подготовка (в силу ее всеобщности) зачастую приводит к рациональным дробям, интегрирование которых достаточно сложно и громоздко. Кроме того, во многих случаях к цели приводят более простые методы. Приведем некоторую классификацию частных случаев.

Интегралы вида .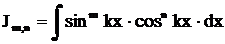

Здесь возможны следующие случаи.

1. Оба показателя степени: m и n – четные положительные числа (один из них может быть нулем). Тогда к цели приводят так называемые формулы понижения степени:

.

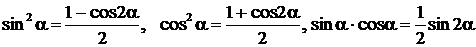Пример.Найти интеграл .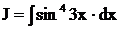

Так как 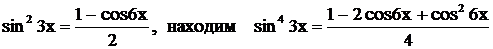и заменяем .

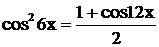После упрощений получим ,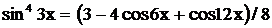

.

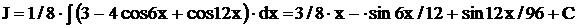2. Хотя бы одно из чисел m или n – нечетное положительное число. Тогда применяем метод отщепления от нечетной степени и используем формулы .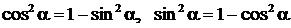

Пример. Найти интеграл .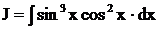

Решение.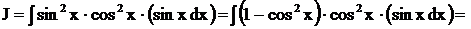

.

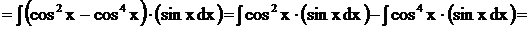
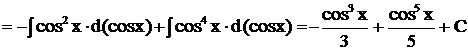Пример. Решите самостоятельно .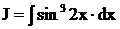

3. Если m и n – целые отрицательные числа одинаковой четности,то к цели

приводит метод отщепления.

Пример. .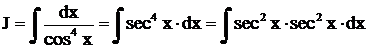

Решение. .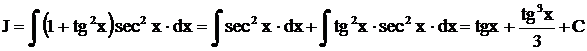

4. В некоторых случаях эффективно использование тождества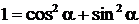

или даже .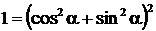

Пример.Найти интеграл .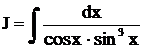

Решение.

,

,

.

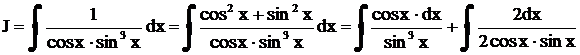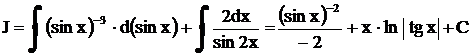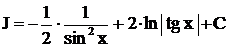Интегралы вида 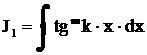, , 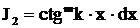где m – целое положительное число, находятся с помощью тождеств , .

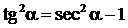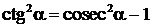Пример.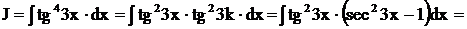

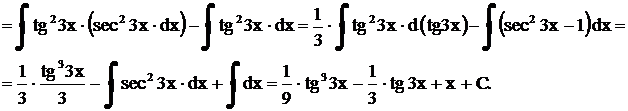
Пример. Найти интеграл .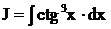

Решение.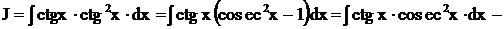

.

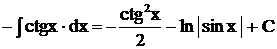Следующие три интеграла берутся с помощью известных формул тригонометрии ,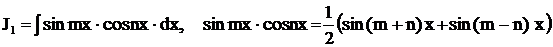

,

.

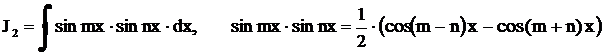Пример. Найти интеграл .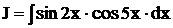

Решение.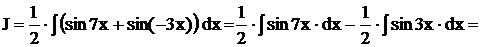

, .

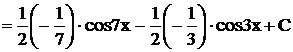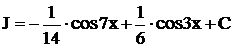Подстановка 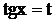рекомендуется для нахождения интеграл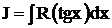а , а

также в тех случаях, когда в интеграле 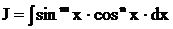числа m и n - четные (положительные или отрицательные). Здесь используются известные формулы тригонометрии: .

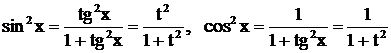Пример.Найти интеграл .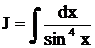

Решение. ,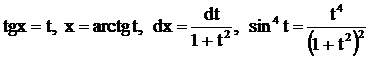

,

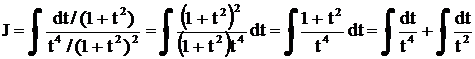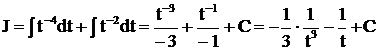. Так как 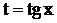, то окончательно

получим .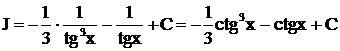

Замечание. Для интегралов 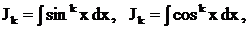где k- натуральное число, методом интегрирования по частям можно получать рекуррентные соотношения, приведенные в таблице интегралов.

Решить самостоятельно

, .

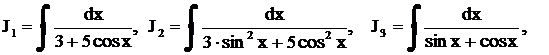
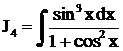Выше были рассмотрены основные приемы и формулы для нахождения неопределенных интегралов. Следует отметить, что многие функции не интегрируются в конечном виде. Так, например, функция 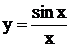непрерывна в промежутке 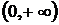, однако, интеграл от нее 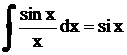(интегральный синус) не выражается в конечном виде через элементарные функции. То же самое относится к

интегралам 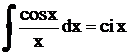(интегральный косинус), 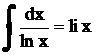(интегральный

логарифм).

Замечание. Во многих случаях заданный интеграл 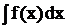может быть найден различными способами. Так, например, интеграл 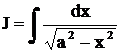с помощью подстановки 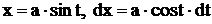дает , где , 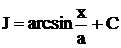. С другой стороны, если возьмем подстановку 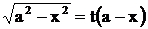, то .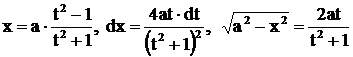

Поэтому .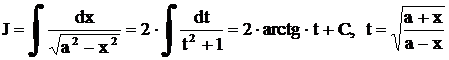

Окончательно 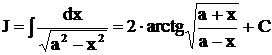. Этот результат лишь формой отличается от предыдущего, так как

.
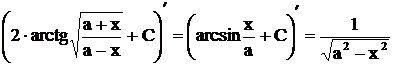