Занятие № 4. Интегрирование рациональных дробей

Цель занятия – научиться разлагать рациональные дроби на простейшие, научиться интегрировать простейшие рациональные дроби.

Изучив оба метода интегрирования: замену переменной и интегрирование по частям, перейдем к нахождению интегралов от различных классов элементарных функций.

Определение. Рациональной дробью называется отношение двух многочленов:

.

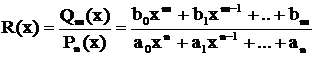В последующем постоянно предполагается, что дробь 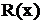несократима, т.е. многочлены 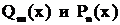не имеют общих корней. Рациональная дробь 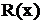называется правильной, если 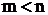, и неправильной, если 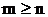. Рассмотрим несколько примеров.

.

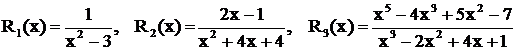Здесь дробь 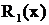правильная, так как 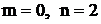; дробь 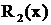также правильная, так как 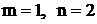; дробь 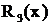неправильная, так как 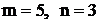. Если дробь неправильная, то, разделив числитель на знаменатель, можно получить целую часть этой дроби – многочлен степени 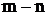, плюс некоторую правильную рациональную дробь. Таким образом, неправильная рациональная дробь представлена в виде

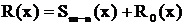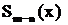, где - многочлен степени 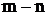, а 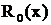- правильная рациональная дробь.

Пример.Выделить целую часть дроби .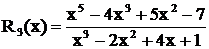

Делим числитель на знаменатель «углом»:

.

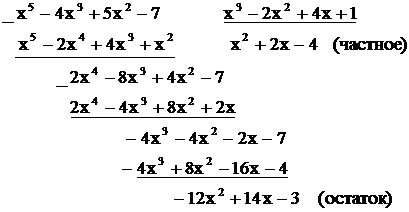
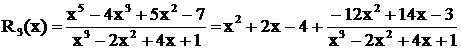Замечание. В простейших случаях, когда, например, 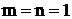, эту работу можно выполнить быстрее:

,

.

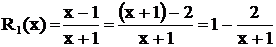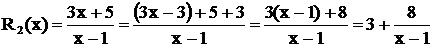Поскольку интегрирование многочлена не представляет труда, то по существу, дело сводится к интегрированию правильных рациональных дробей. Для этого потребуются некоторые новые понятия.

Хорошо известно, что квадратный трехчлен с вещественными корнями 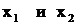разлагается на линейные множители: .

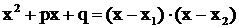В общем случае многочлен степени n разлагается на произведение линейных и квадратных множителей вида

,

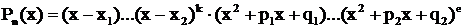причем указанные трехчлены не имеют вещественных корней. При этом говорят, что корень 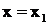- простой, корень 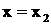имеет кратность к.

Примеры

Многочлен 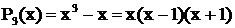имеет простые вещественные корни

.

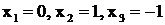Решение. Многочлен 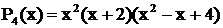имеет вещественный простой корень 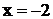; двукратный корень .

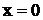Определение. Следующие рациональные дроби называются простейшими первого, второго, третьего и четвертого типов: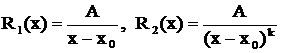

.

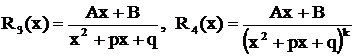Здесь 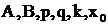- заданные числа, .

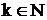В последующем постоянно предполагается, что трехчлен 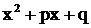не имеет

вещественных корней и, следовательно, не разлагается на линейные множители.

Примеры. Рассмотрим дроби

.

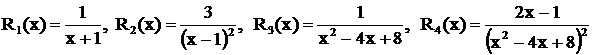Здесь 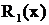- дробь первого типа, причем 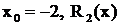- дробь второго типа, где 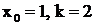. 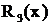- дробь третьего типа, где 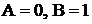, причем трехчлен 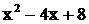вещественных корней не имеет. Дробь 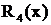принадлежит к четвертому типом, где .

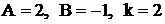Дроб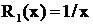и и 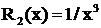принадлежат соответственно к первому и второму типам, причем .

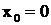Теорема о разложении рациональной дроби. Всякая правильная рациональная дробь разлагается в сумму простейших дробей первого – четвертого типов. При этом если 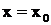- простойвещественный корень знаменателя 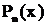, то в разложении ему соответствует дробь первого типа 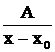; если 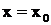- вещественный корень кратностью k, то в разложении ему соответствует сумма k дробей первого и второго типов:

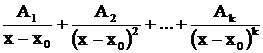; если в знаменателе 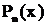имеется трехчлен 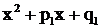без вещественных корней, то в разложении дроби ему соответствует дробь третьего типа 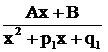; если, наконец, знаменатель 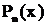содержит множитель 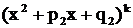, то в разложении ему соответствует сумма «k» дробей третьего и четвертого типов: .

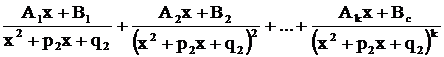Таким образом, разложение дроби 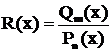существенно зависит от того, какие корни имеет знаменатель 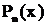. Поэтому разложение рекомендуется проводить по следующей схеме.

1. Найти все корни знаменателя 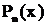и определить их кратность.

2. Написать разложение 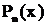на линейные и квадратные множители.

3. Написать сумму простейших дробей в соответствии с полученным разложе-нием знаменателя.

Пример 1. Разложить дробь .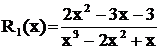

Решение. Здесь знаменатель имеет разложение 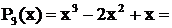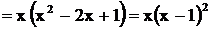. Отсюда следует, что 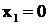- простой вещественный корень, ему соответствует дробь 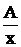; 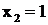- вещественный двукратный корень, ему соответствует сумма дробей 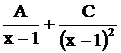. Поэтому данная дробь представлена суммой .

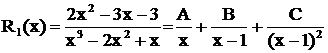Пример 2. Разложить дробь .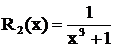

Решение. Здесь 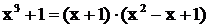, причем трехчлен вещественных корней не имеет, поэтому .

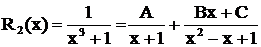Пример 3.Разложить дробь .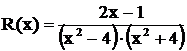

Решение. Здесь знаменатель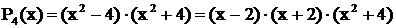

имеет вещественные простые корни: 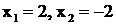. Двучлен 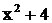веществен-ных корней не имеет: если 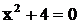, то 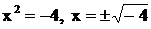. Поэтому разло-жение дроби имеет вид

.

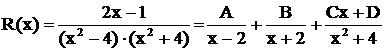Теперь перейдем к нахождению неопределенных коэффициентов разложения: А, В, С,…. Существуют два способа их определения. Поскольку оба способа достаточно простые, рассмотрим их на конкретных примерах.

Первый способ. Дробь 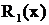представлена в виде

.

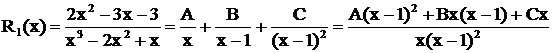Поскольку здесь знаменатели равны, то должны быть равны и числители.

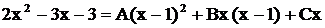. Имеет место равенство двух многочленов, которое выполняется тождественно, т.е. при любых значениям «х».

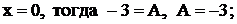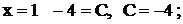Пусть, например, при при 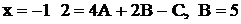. Таким образом, получили разложение дроби .

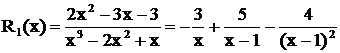Замечание. Нахождение неопределенных коэффициентов А, В, С, … упрощается, если в качестве значений «х» брать корни знаменателя.

Второй способ покажем на следующем примере:

,

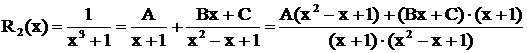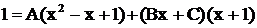. В правой части раскроем скобки и приведем подобные члены, тогда 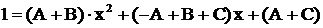или 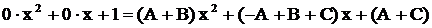. Приравнивая коэффициенты при одинаковых степенях х и свободные члены, получаем систему линейных уравнений относительно А, В, С: 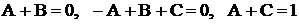. Решив эту систему способом подстановки (или по формулам Крамера), получим 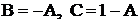. Подставим эти значения во второе равенство: 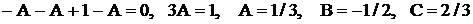. Получаем разложение дроби .

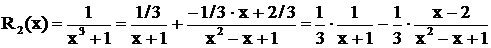Замечание. Результат вычислений всегда можно проверить. Так, в последнем примере .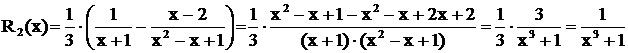

Упражнение. Разложить на простейшие дробь 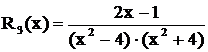. Разложив дробь 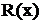на простейшие и проинтегрировав полученное равенство, получим в правой части (в общем случае) сумму следующих четырех интегралов:

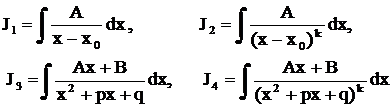
Первый из них по существу табличный: 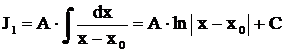. Второй интеграл степенной:

.

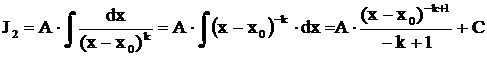Третий интеграл был рассмотрен выше.

Рассмотрим подробнее интеграл 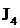, 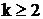. Так как 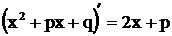, чи-слитель представляем в виде 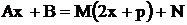, 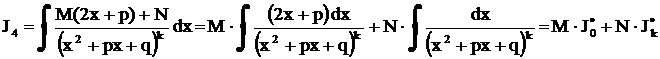. Интеграл 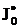степенной, так как

.

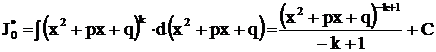Для нахождения интеграла 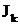выделим из трехчлена полный квадрат:

.

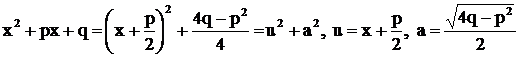Тогда 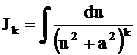. Этот интеграл находится с помощью рекуррентного соотношения (15). Впрочем интеграл может быть найдем с помощью тригонометрической подстановки .

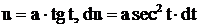Пример. Найти интеграл .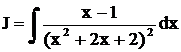

Решение.Так как 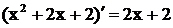, получим .

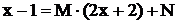Тогда .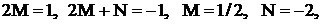

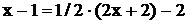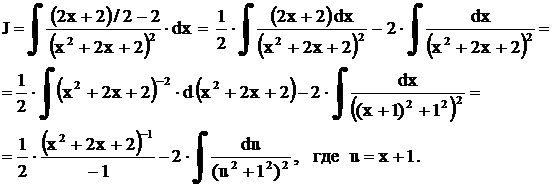
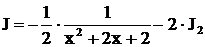. Полагая в формуле (15) 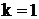, получим

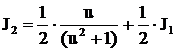, где ,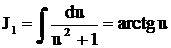

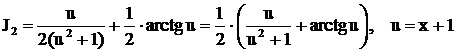. Окончательно находим

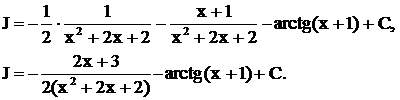
Для сравнения найдем 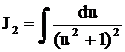, где 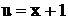с помощью подстановки 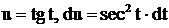. Тогда 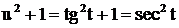. Поэтому

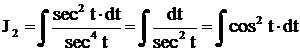. Так как 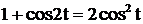, получим

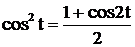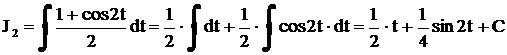, . Из подстановки следует, что ,

,

.

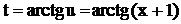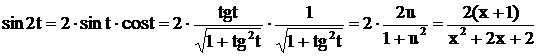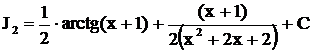Решить примеры

.
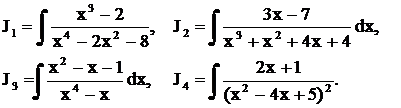