Занятие № 3. Интегрирование по частям

Цель занятия – научиться пользоваться формулой 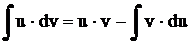и применять ее к каждому из рассмотренных ниже классов функций.

Если заданный интеграл 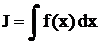не может быть найден рассмотренными выше способами, то подынтегральное выражение 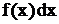разбивают на два сомножителя (u и dv) таким образом, чтобы интеграл 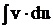был табличным или сводился к табличному. Единого правила для этого не существует, однако можно провести некоторую классификацию интегралов, которые берутся по частям.

1. Интегралы, содержащие произведение многочлена 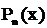на тригонометрические или показательные функции. Более точно к первому классу относятся интегралы вида

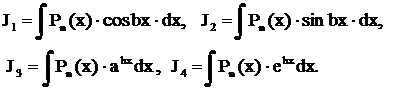
Так как интегралы от 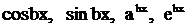по существу табличные, то в этих примерах мешает интегрированию многочлен 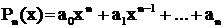. От него можно освободиться путем n-кратного дифференцирования, так как при каждом дифференцировании степень многочлена понижается на одну единицу. Поэтому во всех примерах в качестве функции u берут многочлен, т.е. полагают, что 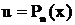. Приведем примеры.

,

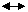
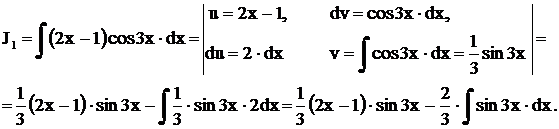
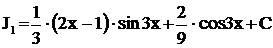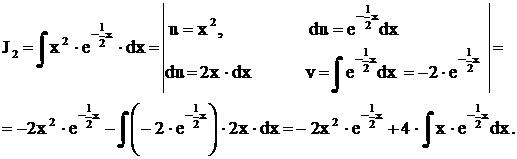
Окончательно можно записать:

,

.

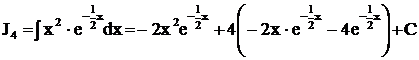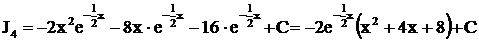Замечание. Обратите внимание, что здесь был дан одночлен второй степени,

т. е. 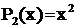. Поэтому формула интегрирования по частям применялась дважды.

2. Так называемые циклические интегралы.К ним относятся интегралы вида

.

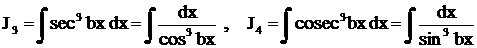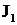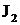В интегралах и надо дважды применить формулу интегрирования по частям, причем разбиение подынтегрального выражения на u и dv можно выполнить

по-разному. Найдем, например, интеграл .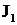

.

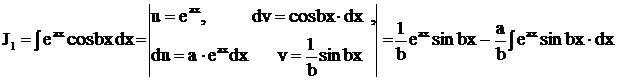Повторяем этот процесс.

.

.

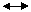
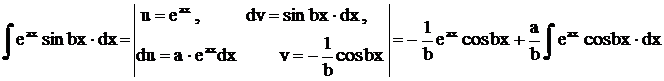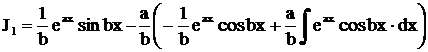Здесь в правой части находится исходный интеграл .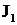

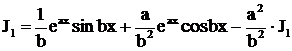. Решив это уравнение относительно 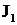, найдем , , .

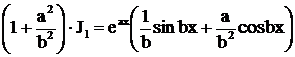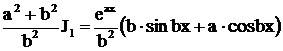Аналогично доказывается, что интеграл 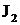определяется формулой

. Для нахождения интегралов 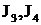достаточно один раз применить формулу интегрирования по частям, а затем воспользоваться формулами тригонометрии. Например,

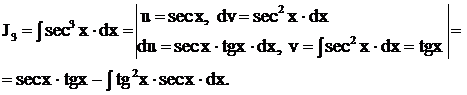
Так как 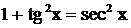, то 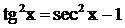, поэтому

,

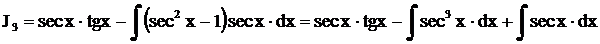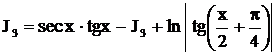.Отсюда следует, что

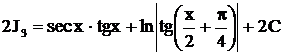
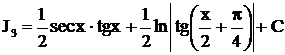. Как видно, циклические интегралы находятся довольно громоздким способом, поэтому они внесены в таблицу интегралов под номерами (11) – (14).

3. К третьему классу относятся некоторые интегралы, содержащие аркусы или логарифмы в сочетании с многочленами: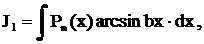

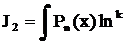
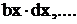Так как в таблице нет интегралов от аркусов или логарифмов, то эти функции надо «убить» с помощью дифференцирования. Поэтому в качестве функции u берем .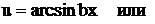

,

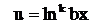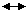
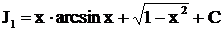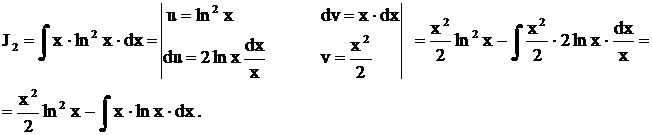
Полученный интеграл снова берем по частям.

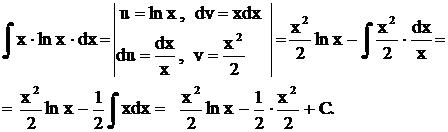
Окончательно получаем ,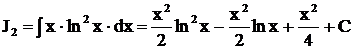

.

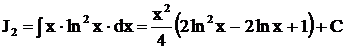Замечание. Указанные три класса не исчерпывают многообразия всех случаев применения формулы интегрирования по частям. Например, интеграл относится к числу циклических. Действительно, полагая

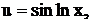
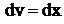получим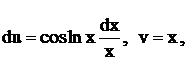

.

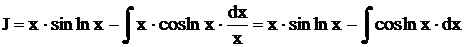Полученный интеграл снова находим по частям

.

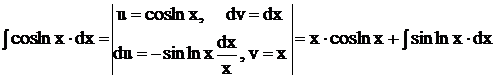Итак, .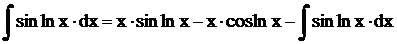

Отсюда , .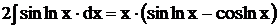

Замечание. Во многих случаях приходится применять оба способа – замену переменной и интегрирование по частям, например,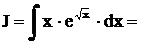

.

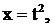
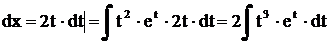Интегрируя по частям трижды, находим, что

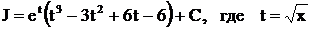. После подстановки

.
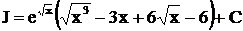