Понятие определенного интеграла.
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
ДЛЯ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
 |

 |
Р Г Г М У
Санкт-Петербург
Одобрено Научно-методическим советом РГГМУ
УДК 51
Веретенников В. Н. Учебно-методическое пособие для выполнения индивидуального задания. Определенный интеграл. – СПб.: Изд. РГГМУ. 2007. – 30 с.
Активизация познавательной деятельности студентов, выработка у них способности самостоятельно решать достаточно сложные проблемы может быть достигнута при такой организации учебного процесса, когда каждому студенту выдаются индивидуальные домашние задания (ИДЗ) с обязательным последующим контролем их выполнения и выставлением оценок.
Предлагаемое пособие адресовано преподавателям и студентам и предназначено для проведения практических занятий и самостоятельных (контрольных) работ в аудитории и выдачи ИДЗ.
© Веретенников В. Н.
© Российский государственный гидрометеорологический университет (РГГМУ), 2007.
ПРЕДИСЛОВИЕ
"Математика" является не только мощным средством решения прикладных гидрометеорологических задач, но также и элементом общей культуры. Именно в рамках математического образования студент получает навыки творческого подхода к решению интеллектуальных проблем, точному пониманию средств возможностей решения проблем, знакомится с современными информационными технологиями.
Целью математического образования является:
1. Воспитание достаточно высокой математической культуры.
2. Привитие навыков современных видов математического мышления.
3. Привитие навыков использования математических методов и основ математического моделирования в практической деятельности.
Воспитание у студентов математической культуры включает в себя ясное понимание необходимости математической составляющей в общей подготовке студента. Он должен выработать представление о роли и месте математики в современной цивилизации и в мировой культуре, уметь логически мыслить, оперировать с абстрактными объектами и быть корректным в употреблении математических понятий и символов для выражения количественных и качественных отношений.
В пособии приведены основные теоретические сведения, отражающие базисные понятия по разделу "Определенный интеграл"; базисные методы решения основных задач; приведен перечень знаний, умений и навыков, которыми должен владеть студент; указана используемая литература.
ПОНЯТИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Аддитивность определенного интеграла
4. Если функция 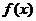 интегрируема на наибольшем из отрезков
интегрируема на наибольшем из отрезков 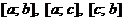 , то она интегрируема на двух других отрезках, причем
, то она интегрируема на двух других отрезках, причем
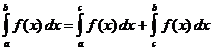
при любом расположении точек 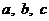 .
.
Интегрирование четных и нечетных функций в пределах симметричных
Приложение определенных интегралов к задачам геометрии
Определенный интеграл, вследствие абстрактности его понятия, широко применяется для вычисления различных геометрических и физических величин.
Величины, которые можно найти с помощью определенного интеграла, должны обладать свойством аддитивности.
Величина 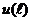 называется аддитивной относительно
называется аддитивной относительно 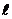 , если
, если
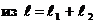 вытекает
вытекает 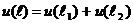 .
.
Аддитивными величинами являются площадь, объем, длина дуги, площадь поверхности вращения, работа, давление и др.
Существуют две схемы применения определенного интеграла для определения различных величин. Одна из них, повторяющая алгоритм получения определенного интеграла по заданной функции, наиболее приемлема в теории. Другая схема носит название дифференциального метода и наиболее приемлема в практике.
Для определения какой-либо величины 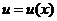 по дифференциальному методу нужно:
по дифференциальному методу нужно:
1. Найти дифференциал этой величины 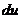 из условий задачи, как главную часть приращения функции
из условий задачи, как главную часть приращения функции 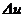
2. Определить пределы интегрирования, если они не заданы, 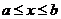 .
.
3. Вычислить интеграл 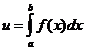 .
.
O a dx b x

Область правильная относительно оси 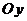 .
.
Если область 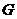 , правильная относительно оси
, правильная относительно оси 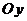 , проектируется на ось
, проектируется на ось 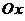 в отрезок
в отрезок 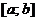 , то ее граница разбивается на две линии: нижнюю границу области, задаваемую уравнением
, то ее граница разбивается на две линии: нижнюю границу области, задаваемую уравнением 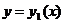 и верхнюю, задаваемую уравнением
и верхнюю, задаваемую уравнением 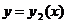 .
.
Тогда область 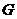 определяется системой неравенств
определяется системой неравенств
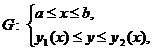
а площадь 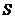 вычисляется по формуле
вычисляется по формуле
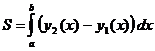 .
.

 y
y




 d
d
 |  |  | ||||||
 |  |  |





 dy
dy 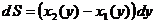




 |  | ||||
 |
 c
c
 |
O x
Область правильная относительно оси 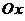 .
.
Если область 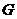 , правильная относительно оси
, правильная относительно оси 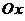 , проектируется на ось
, проектируется на ось 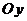 в отрезок
в отрезок 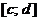 , то ее граница разбивается на две линии: левую границу области, задаваемую уравнением
, то ее граница разбивается на две линии: левую границу области, задаваемую уравнением 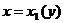 и правую, задаваемую уравнением
и правую, задаваемую уравнением 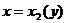 . В этом случае область
. В этом случае область 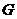 определяется системой неравенств
определяется системой неравенств
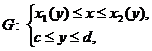
а площадь 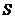 вычисляется по формуле
вычисляется по формуле
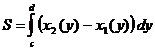 .
.
Задача 7.1.1. Найти площадь фигуры, ограниченной линиями 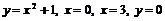 .
.
▲ 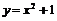 – парабола;
– парабола; 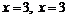 – прямые линии.
– прямые линии.
Найдем точки пересечения данных линий:
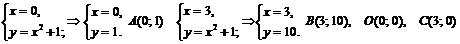
Построение очевидно.
 |
 y
y
 B
B
 |

 A
A


O dx C x
Найдем 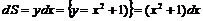 .
.
Область 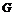 , правильная относительно оси
, правильная относительно оси 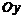 , определяется системой неравенств
, определяется системой неравенств
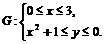
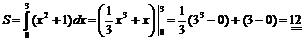 . ▼
. ▼
Замечание. Единицы измерения площадей всюду опускаются (для простоты).
Задача 7.1.2. Найти площадь фигуры, ограниченной линиями 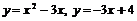 .
.
▲ 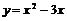 – парабола, которая строится по трем точкам: вершина определяется из условия
– парабола, которая строится по трем точкам: вершина определяется из условия 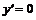 .
.
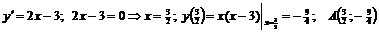 .
.
Точки пересечения с осью 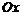 :
: 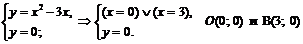 .
.
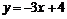 – прямая, которая строится по двум точкам, в качестве которых возьмем точки пересечения данных линий:
– прямая, которая строится по двум точкам, в качестве которых возьмем точки пересечения данных линий: 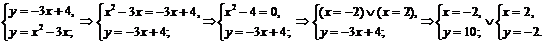
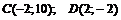 .
.
 |
y

 C 10
C 10
 | |
 | |
 | |
 | |
 |
 4
4
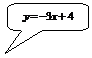 | |||||||||
 | |||||||||
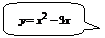 | |||||||||
 |  | ||||||||
 | |||||||||
 |

–2 O dx 2 B x

 A D
A D
1) Имеем: 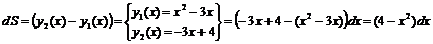 .
.
2) Область 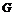 , правильная относительно оси
, правильная относительно оси 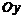 , определяется системой неравенств
, определяется системой неравенств
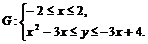
3) 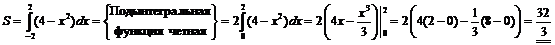 . ▼
. ▼
Задача 7.1.3. Найти площадь фигуры, ограниченную параболой 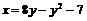 и осью
и осью 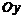 .
.
▲ 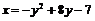 – парабола, которая строится по трем точкам: вершина определяется из условия
– парабола, которая строится по трем точкам: вершина определяется из условия 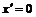 .
.
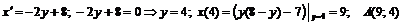
Точки пересечения с осью 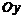 :
:
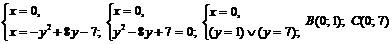 .
.
 |
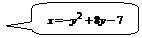 y
y

 C
C

 A
A
dy

 B
B
O x
1) Найдем 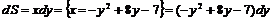 .
.
2) Область 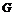 , правильная относительно оси
, правильная относительно оси 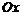 , определяется системой неравенств
, определяется системой неравенств
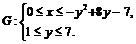
3) 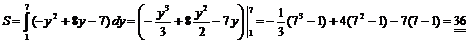 . ▼
. ▼
Задача 7.1.4. Найти площадь фигуры, ограниченной линиями 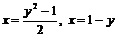 .
.
▲ 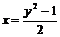 – парабола, которая строится по трем точкам: вершина определяется из условия
– парабола, которая строится по трем точкам: вершина определяется из условия 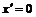 .
.
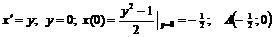 .
.
Точки пересечения с осью 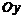 :
:
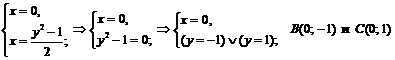 .
.
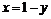 – прямая, которая строится по двум точкам, в качестве которых возьмем точки пересечения данных линий:
– прямая, которая строится по двум точкам, в качестве которых возьмем точки пересечения данных линий:
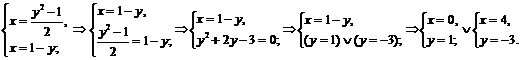
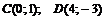 .
.

y
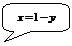 |
C
 A
A
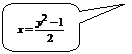 O B 4 x
O B 4 x


 dy
dy
 –3 D
–3 D
1) Имеем 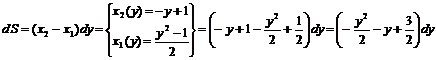 .
.
2) Область 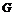 , правильная относительно оси
, правильная относительно оси 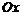 , определяется системой неравенств
, определяется системой неравенств
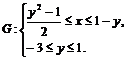
3) 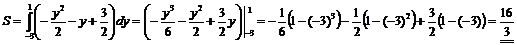 . ▼
. ▼
Вычисление площадей при параметрическом задании линий, ограничивающих фигуру. В задачах такого типа последовательность действий сохраняется, чаще всего усложняется отыскание пределов.
Пусть граница плоской области фигуры 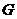 – простая замкнутая кривая, заданная параметрически уравнениями
– простая замкнутая кривая, заданная параметрически уравнениями 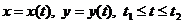 , причем точка
, причем точка 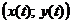 при изменении
при изменении 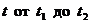 границу области
границу области 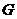 так, что фигура
так, что фигура 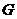 остается слева от движущейся точки. Тогда площадь фигуры
остается слева от движущейся точки. Тогда площадь фигуры 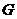 может быть вычислена по любой из следующих формул:
может быть вычислена по любой из следующих формул:
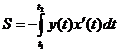 ,
,
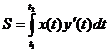 ,
,
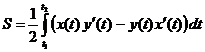 .
.
Задача 7.1.5. Найти площадь эллипса: 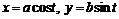 .
.
▲ Чертеж очевиден.
 y
y


 b
b
 |
O dx a x
1) Имеем 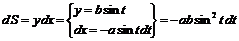 .
.
2) С учетом свойств симметрии фигуры при определении 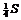 пределы находим по изменению
пределы находим по изменению 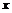
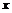 | 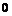 | 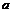 |
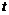 | 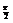 |
3) 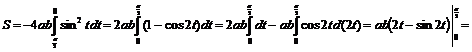
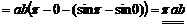 . ▼
. ▼
Вычисление площадей в полярной системе координат. Вычисление площадей в полярной системе координат производится по дифференциальному методу без каких-либо изменений в его операциях и их последовательности.
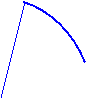
Дифференциалом площади в полярной системе координат является площадь кругового сектора с бесконечно малым центральным углом 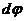 и переменным радиусом
и переменным радиусом 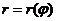 :
:
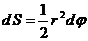 .
.
Форма записи дифференциала площади зависит от способа задания фигуры в полярной системе координат.
 I.
I. 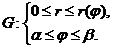 II.
II. 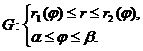
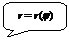 | |||||
 | |||||
 | |||||

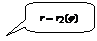


 dφ dφ
dφ dφ
 | |||
 |



 β β
β β
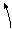
 α α
α α


O p O p
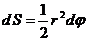
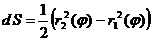
Задача 7.1.6. Найти площадь фигуры, ограниченной лемнискатой Бернулли 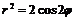 .
.
▲ Напоминаем, что в полярной системе координат чертеж строится по точкам.
Сначала выясняется, где расположена линия по признаку 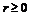 :
:
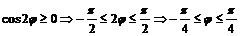 .
.
Затем по периодичности косинуса находим количество петель. Здесь их 2.
Находится 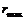 по условию
по условию 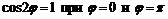 .
.
Построение графика очевидно.
 |
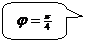




 O 2 p
O 2 p
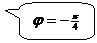 |
Далее все операции совпадают с действиями, рассмотренными раньше.
1)  .
.
2) Пределы по условию существования функции 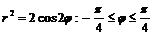 .
.
Или с учетом свойств симметрии фигуры при определении 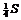 пределы находим:
пределы находим: 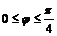 .
.
3) 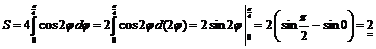
Замечание. Кривые вида  называются розами. Розы имеют
называются розами. Розы имеют 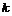 лепестков (петель), если
лепестков (петель), если 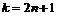 , и
, и 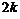 петель, если
петель, если 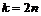 .
.
Например, 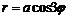 – трехлепестковая роза,
– трехлепестковая роза, 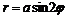 – четырехлепестковая роза.
– четырехлепестковая роза.
При вычислении площадей, ограниченных розами, достаточно найти площадь одного лепестка и затем ее умножить на число лепестков.
ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ
1. Длина кривой.
Рассмотрим на плоскости кривую 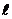 , заданную параметрически:
, заданную параметрически:
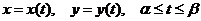 ,
,
где 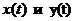 – непрерывные функции на отрезке
– непрерывные функции на отрезке 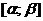 , причем различным значениям
, причем различным значениям 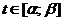 соответствуют различные точки
соответствуют различные точки 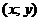 (т. е. нет кратных точек). Такую кривую назовем простой (плоской) незамкнутой кривой.
(т. е. нет кратных точек). Такую кривую назовем простой (плоской) незамкнутой кривой.
Если точки 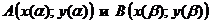 совпадают, а остальные точки не являются кратными, то кривая
совпадают, а остальные точки не являются кратными, то кривая 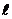 называется простой замкнутой кривой.
называется простой замкнутой кривой.
Длина дуги – аддитивная величина, следовательно, ее можно найти с помощью определенного интеграла.
Воспользуемся дифференциальным методом.
1. Найти дифференциал дуги 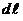 в зависимости от способа задания кривой.
в зависимости от способа задания кривой.
2. Определить пределы интегрирования.
3. Вычислить интеграл от дифференциала дуги.
2. Длина кривой в декартовых координатах. Если кривая задана уравнением
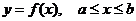 ,
,
причем функция 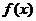 имеет на отрезке
имеет на отрезке 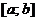 непрерывную производную, то дифференциал дуги вычисляется по формуле
непрерывную производную, то дифференциал дуги вычисляется по формуле
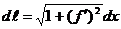 ,
,
а длина кривой по формуле
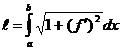 .
.
Если кривая задана уравнением
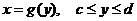 ,
,
причем функция 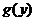 имеет на отрезке
имеет на отрезке 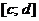 непрерывную производную, то дифференциал дуги вычисляется по формуле
непрерывную производную, то дифференциал дуги вычисляется по формуле
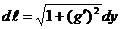 ,
,
а длина кривой по формуле
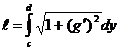 .
.
3. Длина кривой, заданной параметрически. Пусть кривая 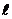 задана параметрическими уравнениями
задана параметрическими уравнениями 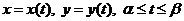 , причем функции
, причем функции 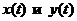 имеют на отрезке
имеют на отрезке 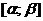 непрерывные производные. Тогда дифференциал дуги выражается формулой
непрерывные производные. Тогда дифференциал дуги выражается формулой
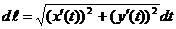
а длина кривой
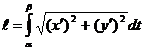 .
.
4. Длина кривой в полярных координатах. Если кривая задана уравнением 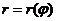 ,
, 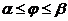 , причем функция
, причем функция 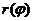 имеет на отрезке
имеет на отрезке 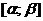 непрерывную производную, дифференциал дуги выражается формулой
непрерывную производную, дифференциал дуги выражается формулой
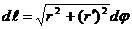 ,
,
а длина кривой
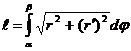 .
.
Замечание. Задачи на вычисление длин дуг можно решать без чертежа.
Задача 7.3.1. Найти длину дуги кривой 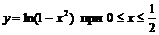 .
.
▲ 1. 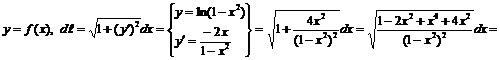
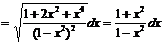 .
.
2. Пределы заданы в условии задачи 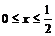 .
.
3. 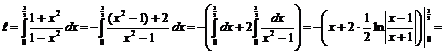
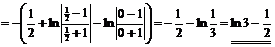 . ▼
. ▼
Задача 7.3.2. Вычислить длину дуги одной арки циклоиды 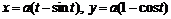 .
.
▲ Кривая задана параметрически.
1. 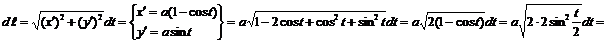
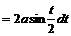 .
.
2. Пределы для переменной 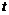 определяются по пределам
определяются по пределам 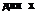 из уравнения
из уравнения 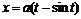
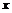 | 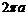 | |
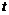 | 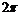 |
3. 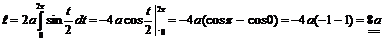 . ▼
. ▼
Задача 7.3.3. Вычислить длину логарифмической спирали 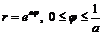 .
.
▲ Кривая задана в полярной системе координат.
1. 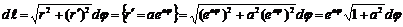 .
.
2. Пределы заданы по условию задачи: 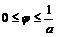 .
.
3. 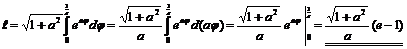 .
.
Решение задачи III типового варианта
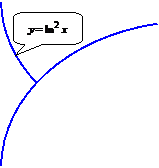
Вычислить (с точностью до двух знаков после запятой) площадь фигуры, ограниченной указанными линиями 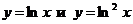 .
.
▲ Найдем точки пересечения данных кривых:
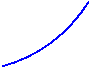
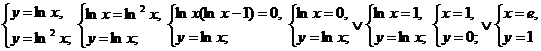
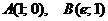 .
.
Сделаем чертеж.
 y
y
 |
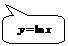


 1 B
1 B
 |
A
 O 1 dx e x
O 1 dx e x
1. Имеем: 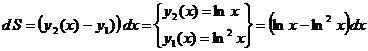 .
.
2. Пусть область 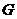 правильная относительно оси
правильная относительно оси 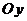 :
:
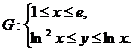
3. 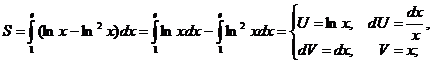
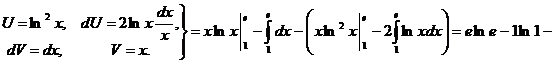
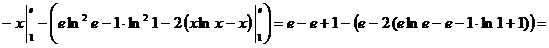
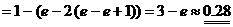 . ▼
. ▼
Решение задачи IV типового варианта
Вычислить (с точностью до двух знаков после запятой) объем тела, полученного вращением вокруг оси абсцисс плоской фигуры, ограниченной параболами 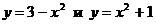 .
.
▲ 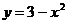 – парабола, строится по трем точкам:
– парабола, строится по трем точкам:
Вершина определяется из условия 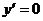 .
.
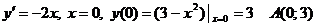 .
.
Точки пересечения с осью 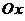 .
.
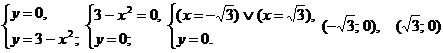 .
.
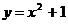 – парабола. Вершина определяется из условия
– парабола. Вершина определяется из условия 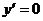 .
.
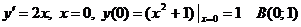 .
.
Точек пересечения с осью 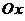 нет
нет 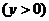 .
.
Находим точки пересечения данных парабол:
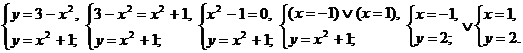
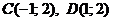 .
.
 |
y
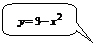 | |||
 |

 A
A
 |
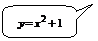
 C D
C D

B

 dx x
dx x
 |
1. Дифференциал объема:
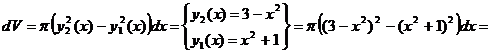
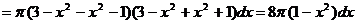 .
.
2. Пределы определяем из решения системы (пересечения парабол): 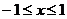 .
.
3. 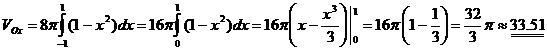 . ▼
. ▼
Знания и умения, которыми должен владеть студент
Умения в решении задач
Студент должен уметь:
1. Вычислять простые определенные интегралы, используя формулу Ньютона-Лейбница, замену переменной, формулу интегрирования по частям.
2. Вычислять по определению или устанавливать сходимость (расходимость) несобственных интегралов.
3. Строить и использовать формулы для нахождения площадей, длин дуг плоских кривых.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1. Козлов В. Н., Максимов Ю. Д., Хватов Ю. А. Структурированная программа (базис). Типовые задачи для контроля, требования к знаниям и умениям студентов. Учебное пособие. – СПб.: СПБГТУ, 2001. – 56 с.
2. Краснов М. Л. и др. Вся высшая математика: Учебник. Т. 1, 2. – М.: Эдиториал УРСС, 2000. – 328 с.
3. Зорич В. А. Математический анализ, часть 1. – М.: Наука, 1981. – 544 с.
4. Веретенников В. Н. Математический анализ: Учебное пособие (рукопись). – СПб.: РГГМУ, 2006.
5. Рябушко А. П. и др. Сб. индивидуальных заданий по высшей математике: Учебное пособие. Ч. 1. – Мн.: Выш. шк., 1990. – 270 с.
6. Виноградова И. А., Олехник С. Н., Садовничий В. А. Задачи и упражнения по математическому анализу. В 2 кн. – М.: Высш. шк., 2000.
7. Кузнецов Л. А. Сборник задач по высшей математике (типовые расчеты). – М.: Высш. шк., 1986.
СОДЕРЖАНИЕ
Стр.
1. Предисловие …………………………………………………………………………… 3
2. Понятие определенного интеграла. Вычисление определенного интеграла. ……… 4
Решение задач I типового варианта ………………………………………………… 9
3. Вычисление несобственных интегралов……………………………………………… 11
Решение задач II типового варианта ……………………………………………… 14
4. Приложение определенных интегралов к задачам геометрии……………………… 14
Решение задачи III типового варианта ……………………………………………… 25
Решение задачи IV типового варианта ……………………………………………… 26
5. Знания и умения, которыми должен владеть студент ……………………………… 27
6. Использованная литература …………………………………………………………… 28
Учебное издание
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
ДЛЯ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Автор: Веретенников Валентин Николаевич.
Редактор И. Г. Максимова.
ЛЗ № 020309 от 30.12.96
 Подписано в печать ……… Формат
Подписано в печать ……… Формат 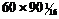 Бумага кн.-жур. Печать офсетная.
Бумага кн.-жур. Печать офсетная.
Печ. л. ……… Уч.-изд. л. ……… Тираж ……… Зак. ………
 |
195196, СПб, Малоохтинский пр. 98. РГГМУ.
Отпечатано …………
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
ДЛЯ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
 |


 |
Р Г Г М У
Санкт-Петербург
Одобрено Научно-методическим советом РГГМУ
УДК 51
Веретенников В. Н. Учебно-методическое пособие для выполнения индивидуального задания. Определенный интеграл. – СПб.: Изд. РГГМУ. 2007. – 30 с.
Активизация познавательной деятельности студентов, выработка у них способности самостоятельно решать достаточно сложные проблемы может быть достигнута при такой организации учебного процесса, когда каждому студенту выдаются индивидуальные домашние задания (ИДЗ) с обязательным последующим контролем их выполнения и выставлением оценок.
Предлагаемое пособие адресовано преподавателям и студентам и предназначено для проведения практических занятий и самос
