Признаки сходимости интегралов 2-го рода.

Для определенности будем рассматривать несобственные интегралы 2-го рода вида 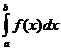= 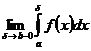.Установленные ниже утверждения легко переносятся на несобственные интегралы 2-го рода вида 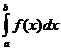= 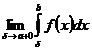и = + .

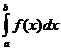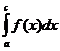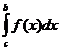Теорема 1.Пусть с – любое число, удовлетворяющее условию a<c<b. Тогда несобственные интегралы 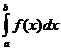и 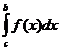сходятся или расходятся одновременно.

Доказательство. Возьмем произвольное число b, удовлетворяющее условию с<b<b. Имеем 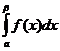=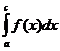+ 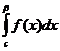(4)

1) Пусть 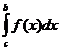сходится Þ существует конечный предел 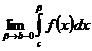. Но тогда из (4) Þ, что существует конечный предел 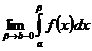Þ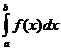сходится.

2) Пусть 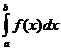сходится Þ существует конечный предел 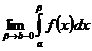. Но тогда из (4) Þ, что существует конечный предел 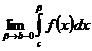Þ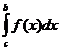сходится.

В случаях 1) и 2) будем имеем: =+.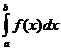

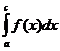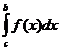3) Пусть 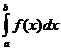расходится. Покажем, что и 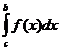расходится.

Допустим, что 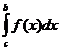сходится. Тогда по пункту 1) должен сходится и 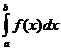. Получили противоречие.

4) Пусть 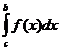расходится. Покажем, что и 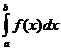расходится.

Допустим, что 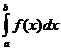сходится. Тогда по пункту 1) должен сходится и 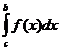. Получили противоречие. Ч.т.д.

Теорема 2. Если f(x)³0 хотя бы для xÎ[с;b) (а£с<b), то для сходимости интеграла 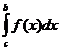(а значит и интеграла 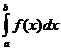) необходимо и достаточно, чтобы существовало число K>0 такое, что 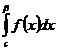£К, для любого bÎ(с;b).

Доказательство. Интеграл 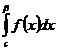=j(b), т.е. представляет собой функцию от b, возрастающую с увеличением b. Для существованию конечного предела у функции j(b) при b®b-0 необходимо и достаточно, чтобы она была ограничена сверху, т.е. чтобы существовало число K>0 такое, чтобы j(b)= 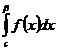£К, для любого bÎ(с;b). Ч.т.д.

Теорема 3 (1-й признак сравнения несобственных интегралов).

Пусть хотя бы для хÎ[с;b) (а£с<b) функции f(x) и g(x) удовлетворяют условию 0≤f(x)≤g(x). Тогда:

1) из сходимости интеграла 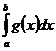(5) следует сходимость интеграла 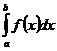(6)

2) из расходимости интеграла 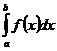следует сходимость интеграла .

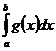Доказательство. Возьмем произвольное число b, такое, что с<b<b

Тогда 0£ 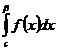£ 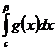(7).

1) Пусть 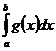сходитсяÞ 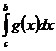сходитсяÞ существует число K>0 такое, что 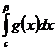£К "bÎ(с;b). Но тогда из (7) следует, что 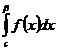£К "bÎ(с;b). Þпо теореме 2: 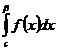- сходитсяÞ 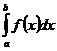- сходится.

2) Пусть 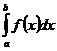- расходится. Нужно доказать, что расходится и 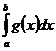. Допустим противное, что 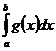сходится. Тогда по пункту 1) должен сходится и 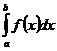. Получили противоречие. Ч.т.д.

Теорема 4. (б.д.) (2-й признак сравнения).Пусть f(x)>0 и g(x)>0 хотя бы для хÎ[с;b) (а£с<b). Пусть существует конечный, отличный от нуля предел

l= 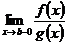(l¹0, l¹¥).

Тогда интегралы 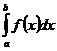и 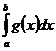сходятся или расходятся одновременно.

Для применения теорем 3 и 4 требуется знание некоторой «эталонной» функции g(x). Часто в этой роли выступает функция g(x)= 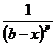(р>0, xÎ[a,b), a<b).

Пример. Исследуем на сходимость интеграл .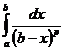

1) Пусть р<1. Тогда

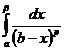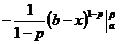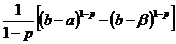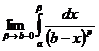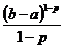= = Þ = Þ

Þ 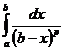сходится при р<1.

2) Пусть р=1. Тогда 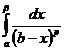= =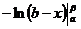ln(b-a)-ln(b-b)Þ 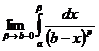=+¥Þ

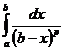Þ расходится при р=1.

3) Пусть р>1. Тогда

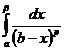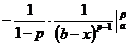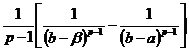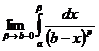= = Þ =+¥Þ

Þ 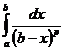расходится при р>1.

Пример.Исследовать на сходимость интеграл I= .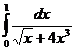

Подынтегральная функция разрывна в точке х=0.

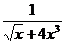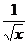< , здесь р= 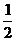<1, следовательно 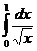сходится. Значит сходится и интеграл от меньшей функции, т.е. .

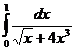Пример. Исследовать на сходимость интеграл I= .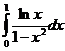

f(x)= 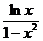определена в промежутке [0,1] всюду, за исключением точек х=0 и х=1. (эти точки – особые). Представим I в виде суммы двух интегралов:

I= 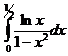+ 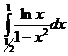=I₁+I₂.

Рассмотрим I₁= 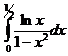. У этого интеграла 1 особая точка х=0. Имеем

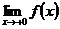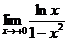= = - ¥Þ f(x) неограниченная в правой полуокрестности точки х=0. Значит I₁ – несобственный интеграл 2-го рода.

Т.к. f(x)= 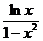~ln x при х®+0, то в качестве функции g(x) возьмем g(x)=ln x. Тогда 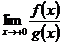= = 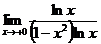=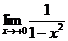1.

Следовательно, несобственные интегралы 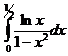и 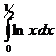в смысле сходимости ведут себя одинаково.

= = = =

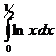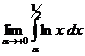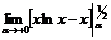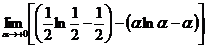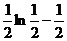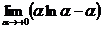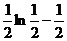= - = -0= .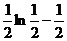

Т.о. 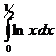сходится. Значит и I₁ сходится.

Рассмотрим I₂= 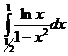. У этого интеграла 1 особая точка х=1. Имеем

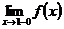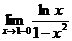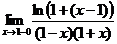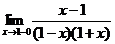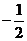= = = = Þ f(x) ограниченная в промежутке 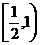. Положим

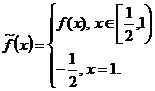
Функция 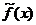ограничена на 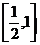Þ 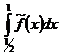существует. Следовательно, I₂= 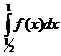сходится.

Т.к. несобственные интегралы I₁ и I₂ сходятся, то сходится и интеграл I= 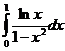.