Вычисление тройного интеграла

1. Вычисление тройного интеграла сведением к повторному

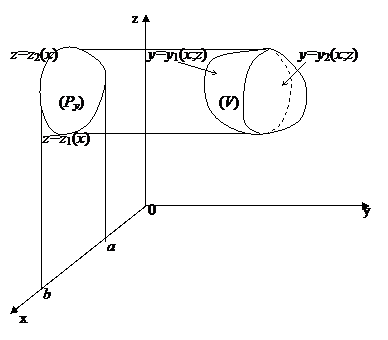
Пусть функция f(x;y;z) непрерывна в некоторой области (V). Пусть поверхность (S), ограничивающая тело (V), пересекается не более чем в двух точках любой прямой, параллельной одной из осей координат (например Oz). Более сложные области сводятся к рассматриваемой путем разбиения на части.

Опишем около тела (V) цилиндрическую поверхность с образующей, параллельной оси Oz. Пусть (P_z) - проекция тела (V) на плоскость XOY. Линия касания этой цилиндрической поверхности с поверхностью (S) разбивает (S) на две части: верхнюю и нижнюю. Пусть нижняя часть поверхности задана уравнением z=z₁(x;y), а верхняя – уравнением z=z₂(x;y), где z₁(x;y), z₂(x;y) - однозначные непрерывные функции, заданные на (P_z). Тогда 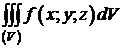сводится к последовательному взятию внутреннего интеграла по переменной z (при постоянных x и y) и внешнего двойного интеграла по области (P_z):

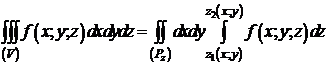Предположим теперь, что область (P_z) тоже имеет простую форму, то есть любая прямая, параллельная оси Oy, пересекает контур области (P_z) не более, чем в двух точках. Через a и b обозначим абсциссы самой левой и самой правой точек на контуре области (P_z). Эти точки делят контур на две части, на одной из которых прямые параллельные оси Oy входят в область (P_z), а на другой – выходят. Каждая из этих частей имеет свое уравнение. Первая: y=y₁(x), вторая: y=y₁(x) (a£x£b). В этом случае

,

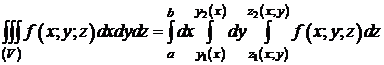то есть тройной интеграл сводится к последовательному вычислению трех определенных интегралов.

Порядок интегрирования может быть другим. Для этого тело (V) надо проектировать на плоскость XOZ или YOZ. Например, спроектируем на XOZ, (Р_у) - проекция на XOZ. Тогда

= =

.

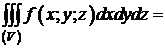
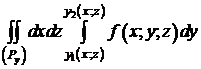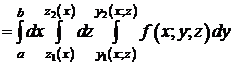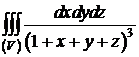Пример 1.Вычислить , где (V) - тетраэдр, ограниченный плоскостями x=0, y=0, z=0 и x+y+z=1.

D Спроектируем телона плоскость XOY. Проекция P - треугольник со сторонами x=0, y=0, x+y=1. Если x и y – фиксированные, то точка может перемещаться от плоскости z=0 (XOY)до плоскости x+y+z=1. Отсюда z=1-x-y. Итак, если (x;y)Î(V), то 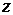изменяется от 0 до 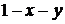. Следовательно, .

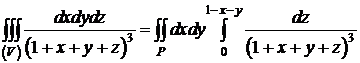Сведем двойной интеграл к повторному.

Если 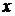- фиксировано (0£х£1) то 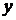может изменяться от прямой 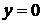(ось Ох) до прямой y+x=1 (y=1-x). Следовательно,

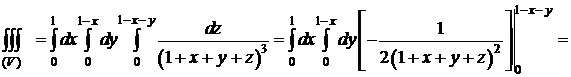
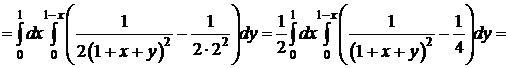
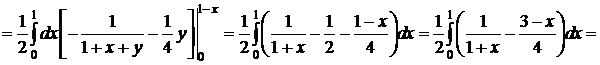
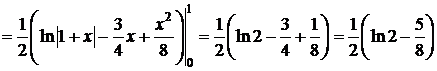. D

2. Тройной интеграл в цилиндрических и сферических координатах

Как и для двойного интеграла, для тройного интеграла имеют место формулы перехода от прямоугольных координат к новым системам координат. Наиболее употребительные из них – цилиндрические и сферические.

I. Цилиндрические координаты

Пусть M₁ - проекция точки M на плоскость XOY, r=OM₁- полярный радиус точки M₁, q=ÐxOM₁- полярный угол точки M₁, z – аппликата точки M. r, q, z называются цилиндрическими координатами точки M. 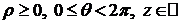. Обозначается M(r;q;z).

Связь с x, y, z: x=rcosq, y=rsinq, z=z.

Следовательно, преобразование тройного интеграла к цилиндрическим координатам происходит так же, как и преобразование двойного интеграла к полярным координатам.

Формула перехода к цилиндрическим координатам в тройном интеграле:

.

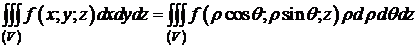Если положить f(x;y;z)=1 всюду в (V), то

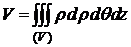- объем тела (V) в цилиндрических координатах.

Выражение 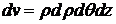называется элементом объема в цилиндрических координатах.

Пример 2.Вычислить объем кругового цилиндра высоты H с радиусом основания R.

D Поместим начало системы координат в центр нижнего основания конуса. Тогда 0£r£R, 0£q<2p, 0£z£H.

.

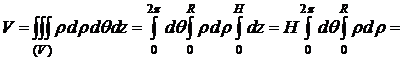
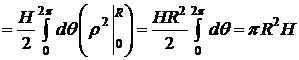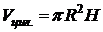(известная формула элементарной геометрии). D

Пример 3.Вычислить объем тела, ограниченного сферой 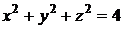и параболоидом .

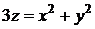D Найдем проекцию линии пересечения сферы и параболоида на плоскость XOY. Для этого из уравнений выразим 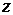и решим систему:

,

,

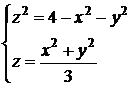
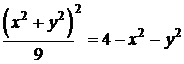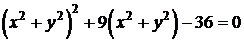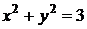или 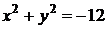- не удовлетворяет условию .

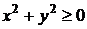Следовательно, линией пересечения поверхностей является окружность 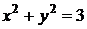, при этом .

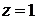Т.к. тело симметрично относительно плоскостей XOY и YOZ, то можно вычислить объем тела 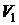, лежащего в I октанте и умножить на 4. Тогда .

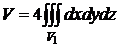Так как проекция тела на плоскость XOY – круг, то следует перейти к цилиндрическим координатам: x=rcosq, y=rsinq, z=z.

Преобразуем уравнения границ:

,

.

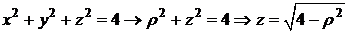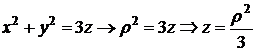Уравнения границы проекции: .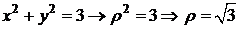

Итак, в области 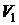: 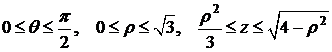. Следовательно,

=

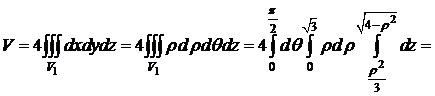
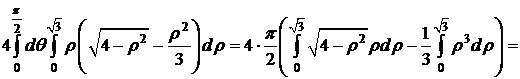
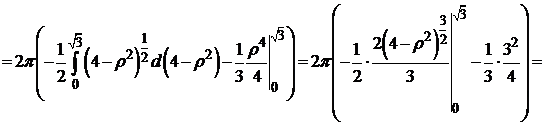
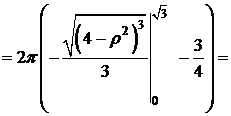
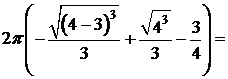
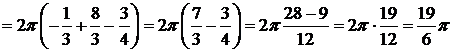. D

II. Сферические координаты

Сферическими координатами точки называются: ОМ=r - расстояние от точки 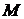до начала координат, j=ÐxOM₁ - угол между Ox и проекцией отрезка 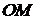на плоскость XOY, q=ÐzOM - угол между осью Oz и отрезком OM: М(r;j;q), r³0, 0£j<2p, 0£q£p.

Связь с прямоугольными координатами:

z=rcosq (из DzOM),

OM₁=rsinq (из DzOM, zM=OM₁),

x=OM₁cosj Þ x=rsinqcosj (из DxOM₁),

y=OM₁sinj Þ y=rsinqsinj (из DxOM₁, xM₁=Oy).

Итак, x=rsinqcosj, y=rsinqsinj, z=rcosq.

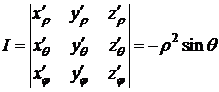. (Вычислить самостоятельно.)

Формула перехода в тройном интеграле к сферическим координатам:

.

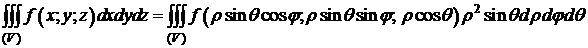Если положим здесь f(x;y;z)=1 всюду в ( 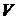), то получим

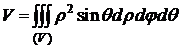- объем тела (V) в сферических координатах.

Выражение 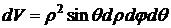называется элементом объема в сферических координатах.

Пример 4.Вычислить объем шара радиуса R.

D Поместим начало системы координат в центр шара. Тогда 0£r£R, 0£q<2p, 0£q£p.

.

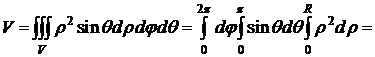
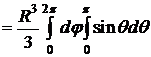
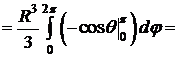
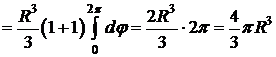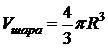(известная из элементарной геометрии формула). D