Функций нескольких переменных

Интегральное исчисление

Функций нескольких переменных

I. Двойной интеграл

Понятие двойного интеграла

1. Квадрируемые фигуры и их площади

Определение.Плоской фигурой F называетсяограниченная замкнутая область из 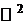. Множество всех граничных точек фигуры F называется её границей и обозначается .

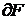Определение.Многоугольником называется плоская фигура, ограниченная замкнутой ломаной.

Многоугольная фигура P – объединение нескольких многоугольников.

Понятие площади многоугольной фигуры и её свойства известны (из курса геометрии). Площадь обозначим .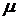

Свойства площади многоугольной фигуры

1. .
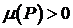2. Если 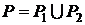, и P₁ и P₂ не имеют общих внутренних точек, то 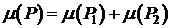(аддитивность).
3. Если P₁=P₂, то 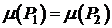(инвариантность).
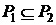4. Если то 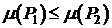(монотонность)

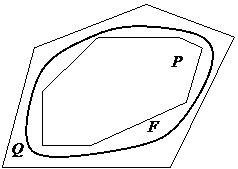Пусть дана плоская фигура F, ограниченная одной или несколькими замкнутыми кривыми. Рассмотрим всевозможные многоугольные фигуры Р, целиком содержащиеся в F, и многоугольные фигуры Q, целиком содержащие в себе F: 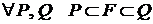. Для их площадей справедливо .

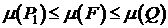Рассмотрим 2 числовых множества: 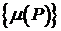и 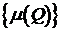. Множество 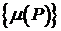ограничено сверху любым числом из 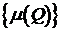. Следовательно, 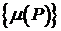имеет верхнюю грань, то есть 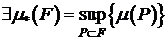. 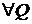выполнено 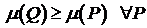. Следовательно, 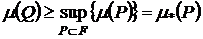, то есть 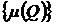ограничено снизу. Следовательно, 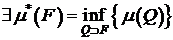. Ясно, что 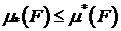. Тогда 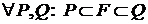выполнено

.

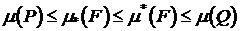Определение.Фигура F называется квадрируемой, если 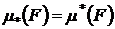. При этом 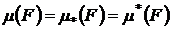называется площадью фигуры F.

Теорема 1(необходимое и достаточное условие квадрируемости). Пусть дана произвольная плоская фигура F. Для квадрируемости плоской фигуры F необходимо и достаточно, чтобы 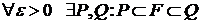, такие, что .

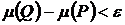Теорема 2.Фигура F квадрируема, если её границу можно разбить на конечное число частей, каждая из которых представляют собой кривую вида y=f(x), xÎ[a;b] или x=φ(y), yÎ[c;d], где f и φ – непрерывные функции.

Определение.Кривая L называется гладкой, если он задана параметрическими уравнениями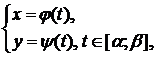

где 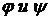определены и непрерывно дифференцируемы на [α;β], и 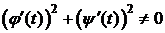"tÎ[α;β].

Кривая называется кусочно-гладкой, если её множество разбить на конечное число гладких кривых.

Теорема 3.Фигура F квадрируема, если её граница является гладкой или кусочно-гладкой кривой.

Площадь плоской фигуры обладает теми же свойствами, что и площадь многоугольной фигуры:

1. .

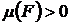2. Если 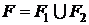, и F₁ и F₂ не содержит общих внутренних точек, то .

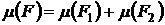3. Если F₁=F₂, то .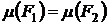

4. Если 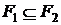то .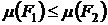

2. Задача об объёме цилиндрического бруса

Пусть тело V ограничено: снизу - плоской фигурой P, лежащей в плоскости XOY, сверху – поверхностью z=f(x;y), где f – неотрицательная и непрерывная на P функция, с боков – цилиндрической поверхностью с образующими параллельными оси OZ. Такое тело называется цилиндрическим брусом. Найдём объём тела V. Разобьём область Р сетью кривых на n частей P₁, P₂,…,P_n. На контуре каждой части P_k построим поверхность с образующей, параллельной оси OZ. Эта поверхность вырежет в теле столбик V_k с основанием P_k. Таких столбиков будет n, и в совокупности они составят всё тело V. Сумма объёмов всех V_k даст объём тела V. Выберем в каждой части P_k произвольную точку 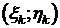и вычислим в ней значение функции 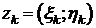. Затем каждый цилиндрический столбик V_k заменим прямым цилиндром с основанием P_k и высотой z_k. Тогда объём цилиндрического столбика V_k приблизительно равен объёму этого прямого цилиндра: .

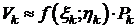Просуммировав эти выражения по 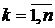, получим объём V:

.

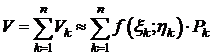Это равенство тем точнее, чем мельче разбиение области P на части P_k.

Диаметром замкнутой области P называется наибольшее расстояние между двумя точками её границы. Пусть 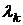-диаметр P_k. Обозначим 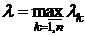. Пусть 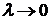, тогда 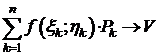то есть

.

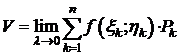3. Определение двойного интеграла

Пусть на замкнутой квадрируемой области P задана функция z=f(x;y). Построим разбиение T области P сетью кривых на n частичных квадрируемых областей P₁, P₂,…,P_n. Площади их также обозначим P₁, P₂,…,P_n. В каждой из частей P_k произвольно выберем точку 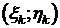и вычислим значение функции в ней. Составим сумму

,

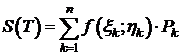которую будем называть интегральной суммой для функции f(x;y) на области Р, соответствующей разбиению T и выбору точек 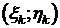. Пусть l_k - диаметр области Р_k, .

Определение 1.Число I называется пределом интегральной суммы S(T) 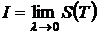, если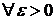 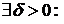для любого разбиения Т области P, такого, что 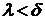и при любом выборе точек 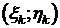ÎР_k выполнено .

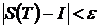Определение 2.Если существует конечный предел интегральной суммы S(T) при 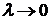, не зависящий ни от способа разбиения T, ни от выбора точек 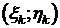, то этот предел называется двойным интегралом от функции f(x;y) по области P и обозначается 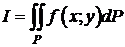или ,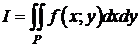

где dP - элемент площади.

Итак, .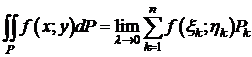

Функция f(x;y) в этом случае называется интегрируемой на области P.

4. Геометрический смысл двойного интеграла

1) Рассматривая задачу об объёме цилиндрического бруса, мы установили что 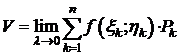. Мы предполагали, что f-непрерывная функция. Так как справа мы имеем предел интегральной суммы S(T) для непрерывной функции, то он существует и равен двойному интегралу от этой функции по области P. Значит, .

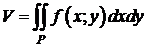Двойной интеграл от неотрицательной непрерывной функции геометрически выражает объем цилиндрического бруса.

2) Если положить f(x;y)=1 всюду в области P, то

,

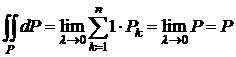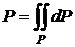- площадь плоской фигуры равна двойному интегралу от 1 по этой области.

5. Ограниченность интегрируемой функции

Теорема 1.Если функция z= f(x;y) интегрируема на области Р, то она ограничена на ней.

Доказательство.

Допустим, что функция не ограничена на области Р. Тогда при любом разбиении области на части функция будет не ограничена хотя бы в одной из её частей. Тогда, выбирая точку 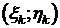произвольно, мы можем сделать 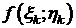сколь угодно большим. Значит, и интегральная сумма S(T) будет сколь угодно большой по абсолютной величине. Следовательно, S(T) не будет иметь конечного предела, и поэтому функция f(x;y) не будет интегрируемой.

Замечание. Обратное утверждение неверно.

Интегральное исчисление

функций нескольких переменных

I. Двойной интеграл

Понятие двойного интеграла

1. Квадрируемые фигуры и их площади

Определение.Плоской фигурой F называетсяограниченная замкнутая область из . Множество всех граничных точек фигуры F называется её границей и обозначается .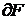

Определение.Многоугольником называется плоская фигура, ограниченная замкнутой ломаной.

Многоугольная фигура P – объединение нескольких многоугольников.

Понятие площади многоугольной фигуры и её свойства известны (из курса геометрии). Площадь обозначим .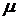

Свойства площади многоугольной фигуры

1. .
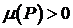2. Если 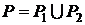, и P₁ и P₂ не имеют общих внутренних точек, то 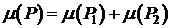(аддитивность).
3. Если P₁=P₂, то 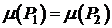(инвариантность).
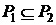4. Если то 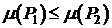(монотонность)

Пусть дана плоская фигура F, ограниченная одной или несколькими замкнутыми кривыми. Рассмотрим всевозможные многоугольные фигуры Р, целиком содержащиеся в F, и многоугольные фигуры Q, целиком содержащие в себе F: 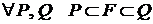. Для их площадей справедливо .

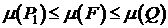Рассмотрим 2 числовых множества: 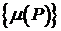и 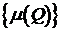. Множество 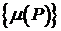ограничено сверху любым числом из 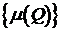. Следовательно, 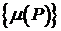имеет верхнюю грань, то есть 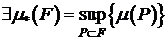. 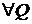выполнено 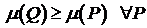. Следовательно, 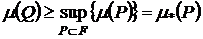, то есть 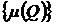ограничено снизу. Следовательно, 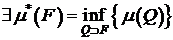. Ясно, что 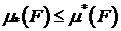. Тогда 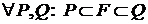выполнено

.

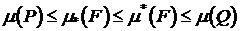Определение.Фигура F называется квадрируемой, если 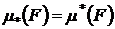. При этом 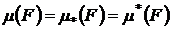называется площадью фигуры F.

Теорема 1(необходимое и достаточное условие квадрируемости). Пусть дана произвольная плоская фигура F. Для квадрируемости плоской фигуры F необходимо и достаточно, чтобы 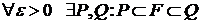, такие, что .

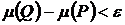Теорема 2.Фигура F квадрируема, если её границу можно разбить на конечное число частей, каждая из которых представляют собой кривую вида y=f(x), xÎ[a;b] или x=φ(y), yÎ[c;d], где f и φ – непрерывные функции.

Определение.Кривая L называется гладкой, если он задана параметрическими уравнениями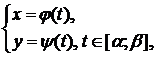

где 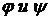определены и непрерывно дифференцируемы на [α;β], и 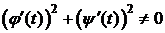"tÎ[α;β].

Кривая называется кусочно-гладкой, если её множество разбить на конечное число гладких кривых.

Теорема 3.Фигура F квадрируема, если её граница является гладкой или кусочно-гладкой кривой.

Площадь плоской фигуры обладает теми же свойствами, что и площадь многоугольной фигуры:

1. .

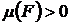2. Если 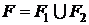, и F₁ и F₂ не содержит общих внутренних точек, то .

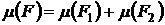3. Если F₁=F₂, то .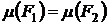

4. Если 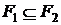то .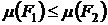

2. Задача об объёме цилиндрического бруса

Пусть тело V ограничено: снизу - плоской фигурой P, лежащей в плоскости XOY, сверху – поверхностью z=f(x;y), где f – неотрицательная и непрерывная на P функция, с боков – цилиндрической поверхностью с образующими параллельными оси OZ. Такое тело называется цилиндрическим брусом. Найдём объём тела V. Разобьём область Р сетью кривых на n частей P₁, P₂,…,P_n. На контуре каждой части P_k построим поверхность с образующей, параллельной оси OZ. Эта поверхность вырежет в теле столбик V_k с основанием P_k. Таких столбиков будет n, и в совокупности они составят всё тело V. Сумма объёмов всех V_k даст объём тела V. Выберем в каждой части P_k произвольную точку 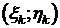и вычислим в ней значение функции 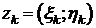. Затем каждый цилиндрический столбик V_k заменим прямым цилиндром с основанием P_k и высотой z_k. Тогда объём цилиндрического столбика V_k приблизительно равен объёму этого прямого цилиндра: .

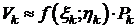Просуммировав эти выражения по 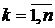, получим объём V:

.

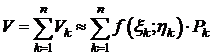Это равенство тем точнее, чем мельче разбиение области P на части P_k.

Диаметром замкнутой области P называется наибольшее расстояние между двумя точками её границы. Пусть 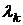-диаметр P_k. Обозначим 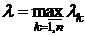. Пусть 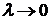, тогда 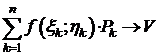то есть

.

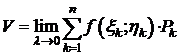3. Определение двойного интеграла

Пусть на замкнутой квадрируемой области P задана функция z=f(x;y). Построим разбиение T области P сетью кривых на n частичных квадрируемых областей P₁, P₂,…,P_n. Площади их также обозначим P₁, P₂,…,P_n. В каждой из частей P_k произвольно выберем точку 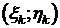и вычислим значение функции в ней. Составим сумму

,

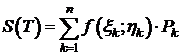которую будем называть интегральной суммой для функции f(x;y) на области Р, соответствующей разбиению T и выбору точек 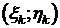. Пусть l_k - диаметр области Р_k, .

Определение 1.Число I называется пределом интегральной суммы S(T) 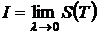, если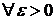 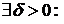для любого разбиения Т области P, такого, что 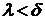и при любом выборе точек 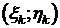ÎР_k выполнено .

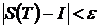Определение 2.Если существует конечный предел интегральной суммы S(T) при 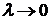, не зависящий ни от способа разбиения T, ни от выбора точек 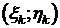, то этот предел называется двойным интегралом от функции f(x;y) по области P и обозначается 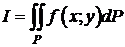или ,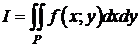

где dP - элемент площади.

Итак, .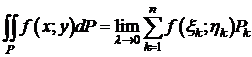

Функция f(x;y) в этом случае называется интегрируемой на области P.

4. Геометрический смысл двойного интеграла

1) Рассматривая задачу об объёме цилиндрического бруса, мы установили что 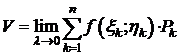. Мы предполагали, что f-непрерывная функция. Так как справа мы имеем предел интегральной суммы S(T) для непрерывной функции, то он существует и равен двойному интегралу от этой функции по области P. Значит, .

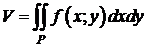Двойной интеграл от неотрицательной непрерывной функции геометрически выражает объем цилиндрического бруса.

2) Если положить f(x;y)=1 всюду в области P, то

,

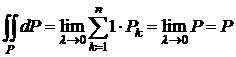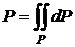- площадь плоской фигуры равна двойному интегралу от 1 по этой области.

5. Ограниченность интегрируемой функции

Теорема 1.Если функция z= f(x;y) интегрируема на области Р, то она ограничена на ней.

Доказательство.

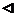Допустим, что функция не ограничена на области Р. Тогда при любом разбиении области на части функция будет не ограничена хотя бы в одной из её частей. Тогда, выбирая точку 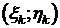произвольно, мы можем сделать 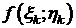сколь угодно большим. Значит, и интегральная сумма S(T) будет сколь угодно большой по абсолютной величине. Следовательно, S(T) не будет иметь конечного предела, и поэтому функция f(x;y) не будет интегрируемой.

Замечание. Обратное утверждение неверно.