Понятие первообразной функции и неопределенного интеграла.
Определение 1.1. Пусть функция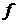 
определена на некотором конечном или бесконечном промежутке Е, то есть на сегменте или полуинтервале числовой оси. Функция 
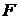, определенная на Е, называется первообразной функции 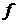на Е, если 
.
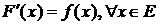Пример 1.1. Функция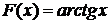 
является первообразной для 
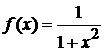на всей числовой прямой, поскольку 
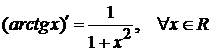. Заметим, что функция 
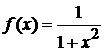, где С—любая постоянная также является первообразной для , так как 
.
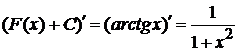Указанное обстоятельство справедливо для любой функции 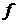, имеющей первообразную. Справедлива следующая теорема:
Теорема 1.1. Пусть функция 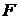какая-нибудь первообразная для функции 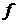на промежутке Е, тогда функция , где С - постоянная, также является первообразной функции 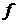на Е. Обратно, всякая первообразная для 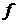на промежутке Е может быть представлена в виде .
Определение 1.2. Совокупность всех первообразных функций, определенных на некотором промежутке Е, называется неопределенным интегралом от функции 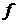на промежутке Е и обозначается 
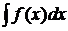. При этом, 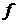называется подынтегральной функцией, а 
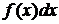-- подынтегральным выражением.
Итак, если 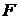-- какая-либо первообразная функции 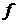на Е , то пишут
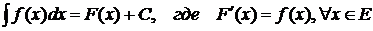(1.1).
Следует иметь ввиду, что не всяка функция 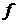имеет первообразную на Е. Однако, если функция 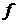непрерывна на промежутке Е, то она имеет на нем первообразную. Далее будем говорить об интегрировании непрерывных функций. В случае разрывной функции речь будет идти лишь об интегрировании ее на одном из промежутков непрерывности.
Учитывая формулу (1.1), запишем таблицу основных неопределенных интегралов, получающуюся непосредственно из соответствующей таблицы производных элементарных функций.
1. 
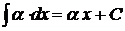, в частности, 
;
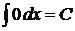2. 
, 
;
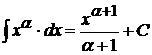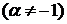3. 
;
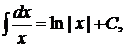
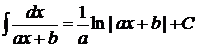4. 
, 
;
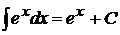5. 
, 
;
6. 
, 
;
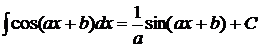7. 
, 
;
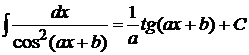8. 
, 
;
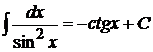9. 
;
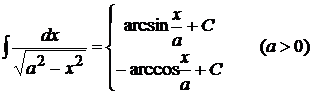10. 
;
11. 
, 
;
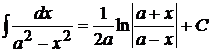12. 
.
Проверьте формулы данной таблицы (они справедливы на тех промежутках, на которых определены входящие в них подынтегральные функции).
Замечание. Все формулы основной таблицы интегралов остаются справедливыми и в том случае, когда переменная интегрирования не является независимой, а представляет функцию от некоторой другой переменной.
Итак, если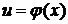 
-- любая дифференцируемая функция и 
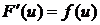, то
.
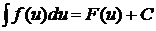Пример 1.2. Вычислить 
.
Так как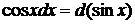 
, то 
.
Этот метод имеет специальное название -- метод интегрирования внесением под знак дифференциала.
Пример 1.3. Вычислить 
.
Постараемся в числителе получить дифференциал знаменателя:
.
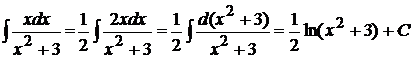Основные свойства неопределенного интеграла.
1). Если функция 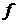дифференцируема на промежутке Е, то
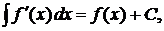а 
.
2). Если функция 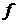имеет на промежутке Е первообразную, то
.
3). Если функция 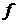имеет первообразную на промежутке Е, то
.
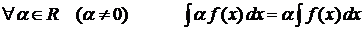4). Если функци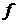и и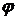 
имеют первообразные на промежутке Е, то
.
Заметим, что свойства 1 и 2 означают, что операции дифференцирования и интегрирования являются взаимно обратными, а поэтому взаимно уничтожают друг друга (если не учитывать постоянного слагаемого).
Основные методы интегрирования.