Реакции системы на одновременное изменение механических и электрических координат

Электромеханическое взаимодействие в ЭМС осуществляется через скорости обобщенных координат 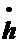и .

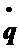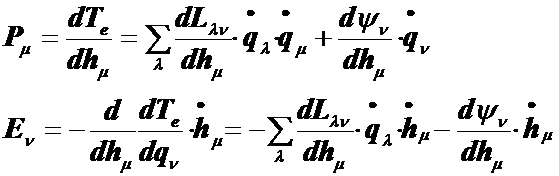(9.46)

Характер взаимодействия определится, если взять производную по электрической скорости от механической силы и производную механической скорости от электрической силы. Получим

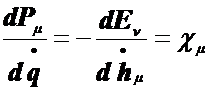(9.47)

Это выражение определяет теорему антисимметрической взаимности электромеханического взаимодействия в магнитном поле, осуществляемой через скорости.

В общем случае 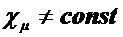, т.е. ЭМС с электромеханическим взаимодействием в магнитном поле описывается нелинейными дифференциальными уравнениями.

ЭМС с электростатическим взаимодействием

Предположим, что электропотенциаль-ная энергия конденсатора зависит от линейной координаты h или угловой координаты g (рис. 9.6).

Тогда электростатическая сила.

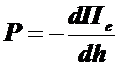(9.48)

Если считать, что величина потенциальной энергии зависит от геометрической координаты h, то для электростатической силы получим

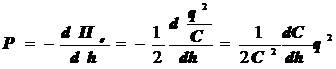(9.49)

Учитывая, что величина емкости определяется формулой

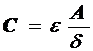(9.50)

и зависит от:

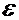- абсолютной диэлектрической проницаемости;

A - общей плоскости двух пластин;

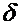- расстояния между ними,

Для емкостной машины

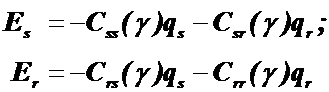(9.55)

В принципе емкостная машина обратима, т.е. она может работать в режиме генератора.

В общем виде уравнения электростатических сил и ЭДС

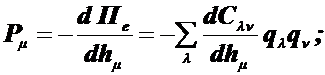(9.56)

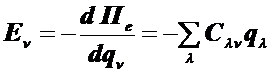(9.57)

Эти уравнения позволяют установить электромеханическое взаимодействие в электрическом поле, осуществляемое по координатам.

Если взять производную от первого выражения по 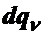, а от второго п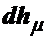о , то

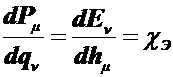(9.58)

Это выражение определяет теорему симметрической взаимности электромеханического взаимодействия в электрическом поле по координатам. Коэффициент 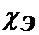позволяет судить о нелинейном характере уравнений.

Уравнения простейших ЭМС

Для вывода уравнений определим выражения для функций, входящих в уравнение Лагранжа-Максвелла: Т, П, D.

(9.60)

Дифференциальные уравнения имеют вид

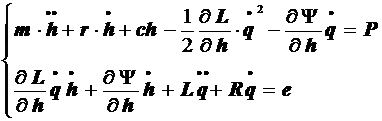(9.61)

Электрические составляющие для электростатических систем

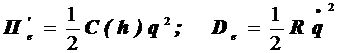(9.62)

В этом случае уравнения будут иметь вид

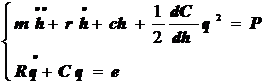(9.63)

Для второй формы записи:

Электрические составляющие для индукционных систем

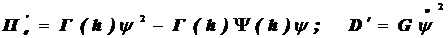(9.64)

Дифференциальные уравнения имеют вид

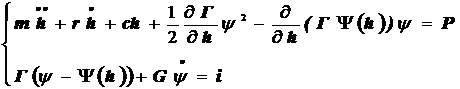(9.65)

Электрические составляющие для электростатических систем

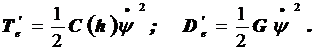(9.66)

Электромагнитные силы

Для изолированного контура с током

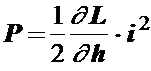
В случае двух индуктивно связанных контуров сила определяется

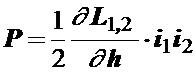
Сила является следствием изменения потокосцепления с внешним магнитным полем.

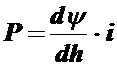
Величина силы определяется по формуле

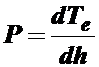
Метод электромеханических аналогий

Уравнения Лагранжа второго рода

Механическая система, имеющая S степеней свободы, описывается уравнениями Лагранжа второго рода:

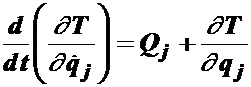. (4.71)

На основе этого уравнения можно записать систему уравнений для s- степеней

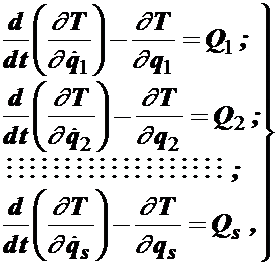(4.72)

которую называют системой уравнений Лагранжа второго рода.