Электрические цепи, эквивалентные механическим системам

Если уравнение электрической цепи отличаются от уравнения механической системы лишь обозначениями, то механическая система эквивалентна электрической цепи. Задача установления графического способа построения схем электрических цепей, эквивалентных механическим системам, возможна при установлении понятия дуальных систем, дуальных графов.

Первая система электромеханических аналогий (табл. 8.4) определяется следующими соответствиями:

скорость v 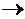сила тока i,

сила p 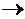ЭДС е (или напряжение u),

а вторая система электромеханических аналогий характеризуется следующими соответствиями:

скорость v 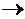напряжение u,

сила p 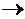сила тока i.

Первая система аналогий позволяет перевести параллельные механические переменные в последовательные электрические, а последовательные - в параллельные.

Вторая система аналогий позволяет перевести параллельные механические переменные в параллельные электрические, а последовательные - в последовательные.

Если представить механическую и электрическую системы графами, то, проведя их анализ, получим следующие результаты. При применении второй системы аналогий граф, описывающий механическую систему, остается неизменным, то есть граф механической системы является также графом электрической цепи. Можно утверждать, что вторая система аналогий не меняет топологическую структуру системы. При использовании первой системы аналогий граф, описывающий механическую систему, является дуальным для графа электрической цепи, эквивалентной механической системе.

В связи с этим вторую систему электромеханических аналогий называют прямой, а первую систему - обратной.

Сформулируем правила графического построения электрических цепей, эквивалентных механическим системам. Если механическую систему представить схемой механических двухполюсников, отражающих характер соединений, то граф, описывающий эту систему может быть получен заменой каждого двухполюсника отрезком, представляющим ребро графа. По второй системе аналогий схему электрической цепи, эквивалентной механической системе, можно получить простой заменой механических двухполюсников электрическими (табл. 8.5).

Схему электрической цепи, эквивалентной механической системе по первой системе аналогий, можно построить, применив правила дуализации и заменяя электрические двухполюсники дуальными (табл. 8.5).

Обобщенные координаты

Обобщенными координатами называются независимые величины, заданием которых однозначно определяется положение всех точек механической системы.

Первоначально в теоретической механике, а впоследствии в теории электричества и электромеханике обобщенные векторы Лагранжа q = [qi, <?2. ., QnV и их производные по времени - обобщенные векторы скорости q = [9j, 2, .. ., qn] -были применены для описания динамики системы. Координаты qi (f=l, 2, ..., п) вектора q называются обобщенными координатами, а координаты qt (f=l, 2, ..., п) вектора q - обобщенными скоростями. С помощью обобщенных координат можно описать, например, перемещение при поступательном движении (производная от перемещения есть скорость), угловое смещение при вращении (в этом случае производная совпадает с угловой скоростью), заряд в электрической цепи (производная от заряда есть ток) или полный поток индукции (производная определяет напряжение). Обобщенные координаты можно определить также и для других систем, однако в более сложных случаях придется использовать несколько различных наборов таких координат. Например, для описания движения в трехмерном пространстве потребуется использовать три обобщенные координаты и соответственно три скорости. Описание электромеханических систем включает обобщенные координаты и скорости, которые содержат две группы переменных для механических и электрических величин.