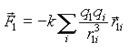Уравнения электромагнитного поля в интегральной форме имеют вид
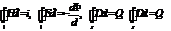
В дифференциальной форме соответственно:
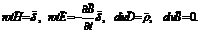
Электростатическое поле.Основные законы.
Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов).
Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга.
Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электрическое поле. Оно определяется через силу, действующую на пробный заряд, помещённый в этом поле. Пробный заряд должен быть малым, чтобы не повлиять на характеристику электростатического поля.
Закон сохранения электрического заряда гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.
Закон сохранения заряда выполняется абсолютно точно. На данный момент его происхождение объясняют следствием принципа калибровочной инвариантности[1][2]. Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу. В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако, такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. То есть был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме.
Закон сохранения заряда в интегральной форме
Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность, можно записать в математической форме:
| |
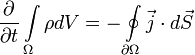
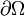— граница этой области, ρ — плотность заряда, 
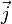— плотность тока (плотность потока электрического заряда) через границу.Закон сохранения заряда в дифференциальной форме
Переходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса можно переписать закон сохранения заряда в локальной дифференциальной форме (уравнение непрерывности)
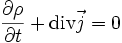
Закон Кулона
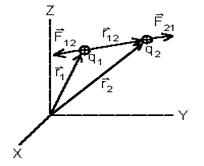
Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с соединяющей заряды прямой.
(1,1)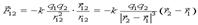 
(1,2)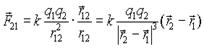 
Здесь k - множитель, зависящий от выбранной системы единиц. В системе СИ его принято записывать как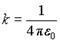 
, где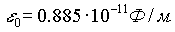 
Закон Кулона установлен экспериментально, но его справедливость подтверждается и тем, что с опытом согласуются все выводы теории, в основе которой лежит этот закон.
Как показывает опыт, сила взаимодействия двух зарядов не изменяется при наличии третьего заряда. Поэтому, независимо от числа зарядов выражения (1.1)-(1.2) можно использовать для вычисления силы взаимодействия каждой пары. Тогда при наличии многих зарядов сила, действующая на заряд 1 со стороны всех остальных зарядов есть
(1,3) 