ЭМС с электростатическим взаимодействием
Предположим, что электропотенциаль-ная энергия конденсатора зависит от линейной координаты h или угловой координаты g (рис. 9.6).
Тогда электростатическая сила.
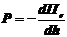(9.48)
Если считать, что величина потенциальной энергии зависит от геометрической координаты h, то для электростатической силы получим
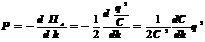(9.49)
Учитывая, что величина емкости определяется формулой
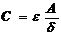(9.50)
и зависит от:
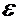- абсолютной диэлектрической проницаемости;
A - общей плоскости двух пластин;
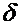- расстояния между ними,
Для емкостной машины
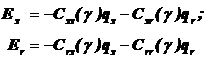(9.55)
В принципе емкостная машина обратима, т.е. она может работать в режиме генератора.
В общем виде уравнения электростатических сил и ЭДС
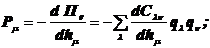(9.56)
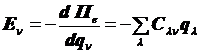(9.57)
Эти уравнения позволяют установить электромеханическое взаимодействие в электрическом поле, осуществляемое по координатам.
Если взять производную от первого выражения по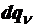 
, а от второго по 
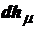, то
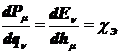(9.58)
Это выражение определяет теорему симметрической взаимности электромеханического взаимодействия в электрическом поле по координатам. Коэффициент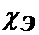 
позволяет судить о нелинейном характере уравнений.
Уравнения простейших ЭМС
Для вывода уравнений определим выражения для функций, входящих в уравнение Лагранжа-Максвелла: Т, П, D.
Рассмотрим простейшую индукционную систему, механические составляющие которой записываются
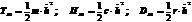(9.59)
Кинетическая энергия и тепловые потери для индукционной системы
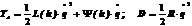(9.60)
Дифференциальные уравнения имеют вид
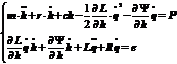(9.61)
Электрические составляющие для электростатических систем
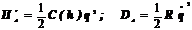(9.62)
В этом случае уравнения будут иметь вид
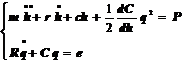(9.63)
Для второй формы записи:
Электрические составляющие для индукционных систем
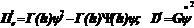(9.64)
Дифференциальные уравнения имеют вид
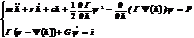(9.65)
Электрические составляющие для электростатических систем
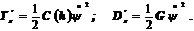(9.66)
Электромагнитные силы
На проводник с током в магнитном поле действуют механические силы, которые называются электромагнитными или электродинамическими. Электромагнитные силы возникают и в одиночном контуре и определяются током в контуре.
Рассмотрим систему, состоящую из n контуров с токами. Положение контуров определяется некоторым числом обобщенных координат h. Механические силы, стремящиеся изменить координаты системы, являются также обобщенными силами.
Пусть под действием силы f некоторая координата h получит приращение dh в направлении действия силы, а остальные координаты остаются неизменными. В этом случае совершается работа fdh. В тоже время произойдет изменение энергии магнитного поля на величину dhWM. Здесь индексом h отмечается, что происходит только одно изменение обобщенной координаты
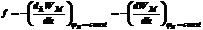. (7.19)
Электромагнитная сила, стремящаяся изменить данную координату системы, равна убыли энергии магнитного поля, отнесенной к единице производимого силой изменения координаты в предположении, что потокосцепления контуров остаются неизменными.
Если функция не зависит от тех или иных переменных, то она называется вырожденной.