Св-ва степенных рядов внутри интерв сходимости

Рассмотр степен ряд

с₀ + с₁ х + с₂ х² + ... + с_{n x}ⁿ + ... ,

имеющ радиус сходимости R>0 (R может= ). Тогда кажд знач х из интерв сход-ти соотв некот сумма ряда. => сумма степенного ряда есть ф-ция от х на интервале сходимости.Обознач ее черезS(x).Тогда можно запис равенство

S(x)=c₀ + c₁ x + c₂ x² +...+ c_n xⁿ +... ,

понимая его в том смысле, что сумма ряда в кажд точке х из интервала сходимости равна знач ф-ции S(x) в эт точке. В этом же смысле будем говорить, что ряд сходится к ф-ции S(x) на интервале сходимости. Вне интервала сходимости равенство не имеет смысла.

Теорема1:Степен ряд в интерв его сходимости можно почленно диф-вать неогранич число раз, причем получающ при этом степенн ряды имеют тот же радиус сходимости, что и исходн ряд, а суммы их соответственно равны S`(x), S``(x), ... , S⁽ⁿ⁾(x).

Теорема 2.Степен ряд можно неогранич число раз почленно интегр-ть в пред-х от 0 до х, если х (-R; R), причем получающ при эт степенные ряды имеют тот же радиус сходимости, что и исходн ряд, а суммы их соответств равны .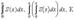

Ряды Тейлора и Маклорена

Ряд Те́йлора—разложф-ции в бесконеч суммустепенных ф-ций. Ряд назван в честь англ математика Брука Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора — его исп ещё в XVII веке Грегори, а также Ньютон. РядыТейлора примен приапроксимации ф-ции многочленами.В частности, линеаризация ур-ий происходит путём разлож в ряд Тейлора и отсеч всех членов выше перв порядка. Пусть ф-ция 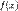бесконечн диф-ема в некотокрестности точки . Формальн ряд

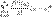наз рядом Тейлора ф-ции 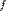в точке .

Ряды Маклорена некот ф-ций

Экспонента:

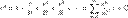
Биномиальное разлож:Квадратный корень:Тригонометрич ф-ции:Гиперболич ф-ции

Разлож элемент ф-ций в степенные ряды

Разлож ф-ции 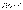в ряд Маклорена.

.

.

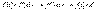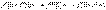Составим для функции 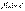формально ряд Маклорена:

.

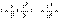образом, имеет место разложение при 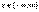: 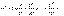33.Применение степенных рядов

Степенные ряды склад, вычит, умнож, в том числе возводятся в квадрат, куб и др степени так же, как многочл, путем приведен подобных членов. При этом, как и многочл, два степенных ряда совпад только,когда совпад их коэффиц при одинак степенях переменой. Деление степенных рядов друг на друга также можно выполнуголком, как деление многочл. Однако удобнее найти частн методом неопред коэффиц: умнож ряд в знаменателе на ряд в прав части равенства и приравнивая коэффиц при одинак степенях x у получ ряда и ряда в числителе. В результате получ бесконечн множ-во ур-ий.

Степенным рядом наз выраж вида рассматр как предел послед-ти многочленов где a0 , a1 , _ - пост числа, наз коэффиц ряда. Числа a0 , a1 , _, x0 и перемx могут быть как действительн, так и комплексн. Заменой x - x0 = y ряд приводится к ряду чисто по степеням y, поэтому без огранич общности можно считать x0 = 0. Действительн ряды - когда коэффиц и переменная суть действительн числа, хотя все приводимые ниже св-ва справедливы и для комплексн рядов.