Линейные однор ур-ия 2 порядкас пост коэфиц
Диф-ное ур-ние второго порядка имеет вид 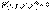 . Опред: Общ реш ур-ния второго порядка наз такая ф-ция
. Опред: Общ реш ур-ния второго порядка наз такая ф-ция 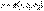 , кот при люб значениях
, кот при люб значениях 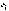 и
и 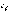 явл решением этого ур-ния. Определение. Линейн однородн ур-ием второго порядка наз ур-ие
явл решением этого ур-ния. Определение. Линейн однородн ур-ием второго порядка наз ур-ие 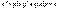 . Если коэффиц
. Если коэффиц 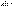 и
и 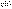 пост, т.е. не завис от
пост, т.е. не завис от  , то это ур-ие наз ур-ием с пост коэффиц и запис его так:
, то это ур-ие наз ур-ием с пост коэффиц и запис его так: 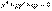 .
.
Лин неоднор ур-ие 2 порядка со спец прав частью
Ур-ие вида y" + py' + qy = f(x), где р и q —вещественныеные числа,f(x)—непрерывн ф-ция, наз линейн неоднородн ур-ием втор порядка с пост коэффиц. Общ реш ур-ния представл собой сумму частн реш неоднородн ур-ния н общ реш соответствующ однородн ур-ия. Нахождение общ реш однородного ур-ния изучено. Для нахождения частн реш воспользуемся методом неопред коэффиц, не содержащим проц интегрирования.
Системы диф ур-ий
Линейн однородн сист с пост коэффиц наз сист диф-ных ур-ний вида:
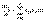 i=1,2,…,n, (11)
i=1,2,…,n, (11)
где коэффиц-ты 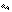 - пост,
- пост, 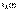 - искомые ф-ции от t.. Сист (11) можно коротко запис ввиде одного матричн ур-ния
- искомые ф-ции от t.. Сист (11) можно коротко запис ввиде одного матричн ур-ния 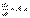 (12), где
(12), где
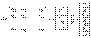 .
.
Теорема. Если сист частных реш однородного ур-ния (12) явл фундаментальной, то общ реш этого ур-ния имеет вид 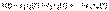 ,
,
где 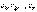 – произвольн постоян.
– произвольн постоян.
Рассмотрим сист диф-ных ур-ий
y'1 = f1(x, y1, y2 , ..., yn),
y'2 = f2 (x, y1, y2 , ..., yn),
..............................
y'n = fn (x, y1, y2 , ..., yn),
где x — независ переменная, а
y1(x), y2(x), ..., yn(x) — неизвестн ф-ции, n — порядок сист. Обозначив
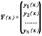
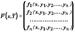
запишем сист в векторной форме
Y '=F(x,Y ).Решением систназ вектор-ф-ция Y , кот определена и нерерывно дифференцируема на интервале(a, b)и удовлетворяет системе, т.е. для всех x0 (a, b) справедливо
Y '(x) =F(x,Y (x)).
Числ ряды. Сходимость и сумма
Числ ряд — это числ послед-ть, рассматриваемая вместе с др послед-тью, кот наз послед-тью частичных сумм (ряда). Рассматриваются числ ряды двух видов. Вещественные числ ряды — изуч в мат анализе;
комплексные числ ряды — изуч в комплексн анализе;
Важнейш вопрос исследования числ рядов — это сходимость числ рядов. Числ ряды применяются вкачестве системы приближений к числам.
Пусть заданы сходящ ряды 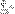 и
и 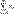 . Тогда: Их суммой наз ряд
. Тогда: Их суммой наз ряд 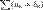
Их произв по Коши наз ряд 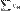 , где
, где 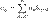
Если оба ряда сходятся, то их сумма сход, если оба ряда сход абсолютно, то их сумма сход абсолютно. Если хотя бы один из рядов сход абсолютно, то произвед рядов сходится.
Признаки сходимости рядов с положит членами
На послед-ти 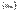 построим частичные суммы построим частичные суммы 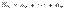 . Cимвол . Cимвол 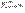 , обозначающ предел частичн сумм ( , обозначающ предел частичн сумм ( 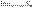 ), наз рядом, где ), наз рядом, где 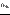 -- общ член ряда.Ряд - знакоположительн, если все -- общ член ряда.Ряд - знакоположительн, если все 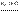 . . |
Замечание1.В матанализе доказывается, что знаконеотрицательн ряд сходится =>частичн суммы ограничены.
Док-во след из теоремы Вейерштрасса о том, что огранич монотонная послед-ть имеет предел.
Лемма 1. Если 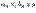 , то из сходимости
, то из сходимости 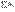 след сходимость
след сходимость 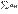 , а из расходимости
, а из расходимости 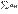 след расходимость
след расходимость 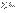 . Док-во. Рассмотр частичн суммы рядов (обозначим их
. Док-во. Рассмотр частичн суммы рядов (обозначим их 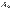 и
и 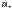 ). Если
). Если 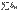 сходится, то постед-ть
сходится, то постед-ть 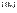 огранич, а раз
огранич, а раз 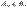 , то
, то 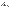 тоже ограничена, т.е.
тоже ограничена, т.е. 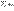 также cходится. Из этого же неравенства следует утверждение о расходимости.
также cходится. Из этого же неравенства следует утверждение о расходимости.
