Оценки ошибок формул трапеций и центральных прямоугольников

Будем предполагать, что функция f(x) имеет на отрезке интегрирования 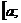. 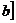вторую производную f//(x), и f//(x)непрерывна на 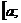. 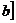, причём 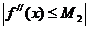при всех x . .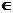

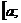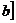Для метода центральных прямоугольников представим ошибку 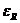в виде суммы ошибок на каждом отрезке разбиения:

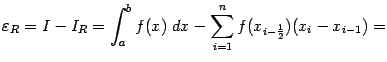
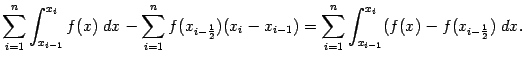
По формуле Тейлора, применённой к функции f(x) в точке 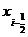, получаем для x . :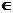

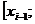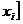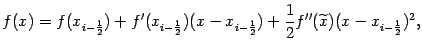
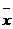
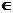
где 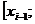. 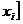— некоторая точка, лежащая между 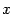и .

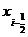Заметим, что

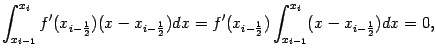
поскольку 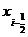— середина отрезка интегрирования в этом интеграле. Получаем тогда, что

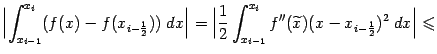
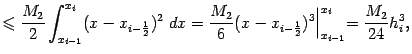
где h_i=x_i-x_i-1. Таким образом, суммируя по всем отрезкам разбиения, получаем оценку ошибки:

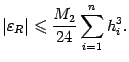
Если все отрезки разбиения имеют одинаковую длину h_i= 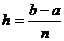, то получаем

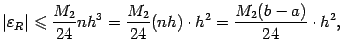
или

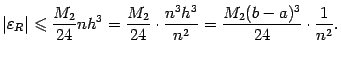
Следовательно, при уменьшении вдвое шага разбиения 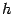, то есть при удвоении числа шагов 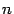, оценка возможной ошибки уменьшается вчетверо, а при уменьшении шага в 10 раз оценка ошибки уменьшается в 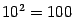раз. Квадратурную формулу, обладающую таким свойством ошибки, называют формулой второго порядка точности. Итак, формула центральных прямоугольников — формула второго порядка точности. Покажем, что формула трапеций также имеет второй порядок точности.

Рассмотрим снова рис. 5. Прямая, соединяющая концы хорды графика, то есть точки (x_i-1;f(x_i-1)) и (x_i;f(x_i)), имеет уравнение

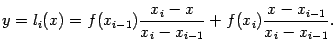
Действительно, это равенство задаёт линейную функцию, и легко проверить, что l_i(x_i-1)=f(x_i-1) и l_i(x_i)=f(x_i). Разность между площадью под графиком функции на отрезке 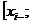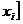,и площадью трапеции S_i равняется тогда

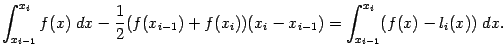
Докажем, что стоящая под знаком последнего интеграла разность удовлетворяет оценке

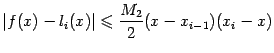
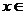
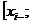
при всех 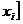,. Эта оценка получается как следствие такой теоремы.

Теорема (о погрешности линейной интерполяции) Пусть f(x) — функция, имеющая на отрезке 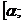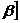непрерывную вторую производную f^//(x), а l(x) — линейная функция, такая что 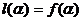; 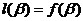. Назовём функцию l(x) линейной интерполирующей функцией для f(x) на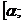 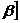, а разность 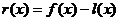погрешностью линейной интерполяции.

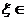
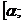
Тогда найдётся такая точка 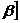, что

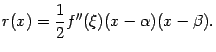(1)

Доказательство. Очевидно, что пр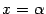и и 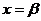равенство (1) выполняется, как бы ни была выбрана точка 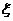, поскольку и левая, и правая части равенства обращаются тогда в ноль. Пусть теперь точка 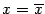не совпадает ни с 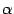, ни с 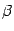. Рассмотрим вспомогательную функцию

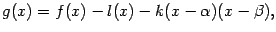
зависящую от параметра 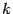, и выберем значение 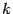так, чтобы было выполнено равенство 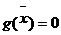. Легко видеть, что для этого нужно взять 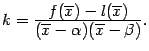Тогда

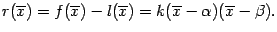
Функция 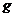(x) обращается в 0 в трёх точках: 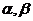и 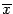. Значит, по теореме Ролля, её производная 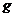^/(x) обращается в 0 в каких-то двух точках 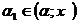и 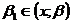. Применяя снова теорему Ролля, теперь уже к производной 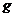^/(x) на отрезке 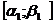, получаем, что 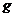^//(x) обращается в 0 в некоторой точке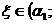 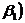. Однако функцию 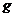^//(x) легко вычислить:

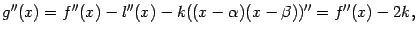
так как вторая производная линейной функции 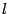равна 0. Таким образом, ,

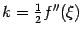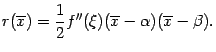
Остаётся заметить, что точка 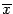выбиралась как произвольная точка интервала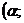 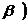, и доказательство завершено.

Возвращаемся к изучению ошибки формулы трапеций и связанным с этим обозначениям.

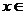
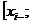
Следствие 1. При 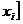имеет место оценка

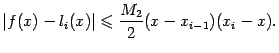
Доказательство. Применим формулу (1) к функции g=f и отрезку 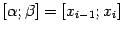и получим:

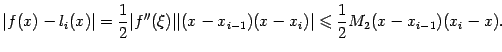
Здесь мы заметили, что xi-1 и xi — корни квадратного трёхчлена (x-xi-1)(x-xi) так, что на отрезке между корнями квадратный трёхчлен не больше нуля, и поэтому

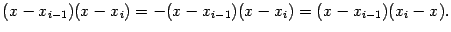
Ошибку на 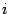-м отрезке разбиения мы можем теперь оценить так:

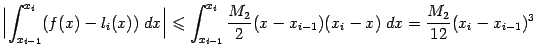
(последний интеграл легко вычисляется).

Просуммируем теперь оценки ошибок на каждом отрезке разбиения и получим оценку ошибки всей квадратурной формулы трапеций:

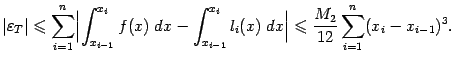
Если длины всех отрезков разбиения взяты одинаковыми, равными 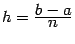, то полученная оценка даёт

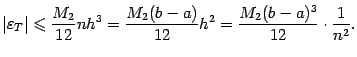
Оценки ошибок 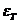и 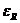, как мы видим, отличаются ровно в два раза. Выше мы отмечали, что эти ошибки имеют противоположные знаки, если функция f//(x)сохраняет знак на отрезке интегрирования. Значит, на каждом отрезке знакопостоянства функции f//(x)ошибк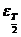и и 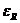будут примерно компенсировать друг друга. Подобно тому, как мы получили формулу трапеций из формул левых и правых прямоугольников, попробуем получить усреднённую квадратурную формулу, скомбинировав формулы центральных прямоугольников и трапеций; при этом нас подогревает надежда на то, что новая формула будет иметь существенно меньшую ошибку. Умножая IR на 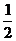, для того чтобы уравновесить ошибки противоположных знаков, получаем:

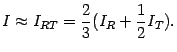
Преобразуем полученную квадратурную формулу, рассмотрев, из каких слагаемых состоит её правая часть. Величины, соответствующие приближённым значениям интеграла по отрезку разбиения 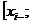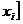, дают

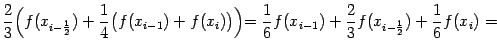
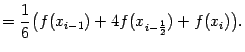
Суммируя эти величины по всем отрезкам разбиения, получаем квадратурную формулу:

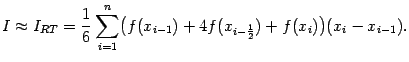(2)

Эта формула в точности совпадает с формулой Симпсона.