Кафедра Холодильных систем и технологий
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ
ФЕДЕРАЦИИ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ
( образован в 1953 году)
_____________________________________________________
Кафедра Холодильных систем и технологий
Холод.-1.22.1706 зчн.плн., Холод.-1.22.1706 зчн.скр.
Дистанционное Холод.-1.22.2701зчн.плн., Холод.-1.22.2701зчн.скр.
обучение Холод.-1.22.2703зчн.плн., Холод.-1.22.2703 зчн.скр.
Холод.-1.22.2704 зчн.плн., Холод.-1.22.2704 зчн.скр.
Холод.-1.22.2704 зчн.плн., Холод.-1.22.2704 зчн.скр.
Холод.-1.22.2705 зчн.плн., Холод.-1.22.2705 зчн.скр.
Холод.-1.22.2707 зчн.плн.,Холод.-1.22.2707 зчн.скр.
Холод.-1.22.2708 зчн.плн., Холод.-1.22.2708 зчн.скр.
Холод.-1.22.2710 зчн.плн., Холод.-1.22.2710 зчн.скр.
Холод.-1.22.2712 зчн.плн., Холод.-1.22.2712 зчн.скр.
Холод.-1.22.3511 зчн.плн., Холод.-1.22.3511 зчн.скр.
В.Ю. Воскресенский, Т.Г.Мороз, В.В.Фадеев
ТЕПЛОТЕХНИКА
Учебно-практическое пособие для студентов технологических специальностей всех форм обучения

www.msta.ru
4330
Москва – 2004
УДК 621.1.01(075.8)
ã Воскресенский В.Ю., Мороз Т.Г., Фадеев В.В. П/ред. В.Ю.Воскресенского. Теплотехника. Учебно-практическое пособие.– М.,МГУТУ, 2004
Учебное пособие предназначено для студентов механических и технологических специальностей, изучающих по системе дистанционного обучения дисциплину “Теплотехника“. В кратком и систематизированном виде, в дополнение к ранее изученным материалам по курсу физики, рассматриваются основные законы технической термодинамики и теории тепло-массообмена. В свете этих законов рассматриваются общие принципы действия, расчета и рационального использования современного теплового и, в меньшей мере, холодильного оборудования, применяемого в том числе и на предприятиях пищевой промышленности. В пособии опущен ряд традиционных тем (политропные процессы, термодинамические потенциалы, основы теории теплового подобия, двигатели внутреннего сгорания и ряд других). Студенты могут при необходимости воспользоваться рекомендованной литературой. Изложение важнейших тем дисциплины сопровождается контрольными вопросами, тренировочными заданиями в виде учебных тестов с объяснением ответов, упражнениями и примерами с подробными решениями.
Пособие предназначено для студентов факультетов Управления и информатизации (спец.1706) и Технологического менеджмента (спец.2701-2712, 3511) 3-го курса полной и 2-го курса сокращенной форм обучения
Авторы: Воскресенский Всеволод Юрьевич (раздел I), Мороз Тамара Георгиевна (раздел II), Фадеев Владимир Васильевич (раздел III).
Рецензенты: Щеренко А.П. проф. д.т.н. директор института оборудования и информационных технологий Московского государственного университета пищевых производств
Мороз С.Ф. доцент кафедры ОКМ, Московского энергетического института (Технического Университета).
Редактор Свешникова Н.И.
ISBN 5 – 89933 – 032 – 5
ã Московский государственный университет технологий и управления, 2004
109004 М., Земляной вал, 73
С о д е р ж а н и е
| Раздел 1.ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА………………………... | |
| 1.Термодинамические параметры состояния………………………………... | |
| 2. Первый закон и уравнение первого закона термодинамики……………... | |
| 3. Открытые термодинамические системы (потоки рабочего тела)………... | |
| 4. Простейшие термодинамические процессы в открытых системах……… | |
| 5.Второй закон термодинамики………………………………………………. | |
| 6.Термодинамические свойства рабочих тел. Пар…………………………... | |
| 7. Термодинамические свойства газов……………………………………….. | |
| 8. Круговые термодинамические процессы рабочих тел в теплосиловых установках и холодильных машинах………………….. | |
| Вопросы для самоконтроля по разделу 1…………………………………….. | |
| Тест по разделу 1………………………………………………………………. | |
| Раздел 2. ТЕПЛОПЕРЕДАЧА……………………………………………… | |
| 1.Теплопроводность…………………………………………………………… | |
| 2.Конвективный теплообмен (теплоотдача)…………………………………. | |
| 3.Теплообмен при изменении агрегатного состояния вещества…………… | |
| 4. Теплопередача ………………………………………………………………. | |
| 5. Теплообмен при излучении ………………………………………………... | |
| 6 Теплообменные аппараты…………………………………………………… | |
| Вопросы для самоконтроля по разделу 2…………………………………….. | |
| Тест по разделу 2………………………………………………………………. | |
| Раздел 3. ПРОМЫШЛЕННАЯ ТЕПЛОЭНЕРГЕТИКА………………… | |
| 1. Топливо. Энергетическое топливо. Виды и назначение топлив…………. | |
| 2. Котельные установки……………………………………………………….. | |
| 3.Паровые котлы……………………………………………………………….. | |
| 4.Водоподготовка……………………………………………………………… | |
| 5. Тепловой баланс котельного агрегата……………………………………... | |
| 6. Отопление, вентиляция и кондиционирование воздуха………………….. | |
| Вопросы для самоконтроля по разделу 3…………………………………….. | |
| Тест по разделу 3………………………………………………………………. | |
| Ответы на вопросы тестов по разделам 1,2,3………………………………... | |
| Решение тренировочных заданий…………………………………………….. | |
| Тест по дисциплине………………………………………………………….... | |
| Вопросы к экзамену……………………………………………………………. | |
| Список рекомендуемой литературы………………………………………….. |
Равновесные состояния
Если внутри термодинамической системы между ее частями нет переноса массы (перемешивания) и переноса энергии (в формах работы или теплообмена), соответственно если система находится в состоянии внутреннего и внешнего покоя, то такую систему называют равновесной. Если неравновесную систему изолировать от внешней среды, то она рано или поздно перейдет самопроизвольно в равновесное состояние.
Мы принимаем также, что равновесное состояние характеризуется также однородностью свойств во всех частях системы и поэтому определяется минимальным числом параметров по сравнению с неравновесным состоянием. В частности, равновесное состояние большинства рабочих тел определяется двумя параметрами состояния. Остальные параметры зависят от первых двух.
Давление
Давление газов, паров измеряют манометрами. Вследствие конструктивных особенностей манометров приходится различать абсолютное и избыточное давление. То давление, которое газ оказывает на стенки сосуда, называют абсолютным. Однако манометры измеряют не абсолютное давление, а разность между абсолютным и атмосферным давлением. Эту разность, т.е. непосредственно показания манометра называют избыточным давлением. Чтобы в практической работе на производстве пользоваться таблицами термодинамических свойств рабочих тел, необходимо уметь переводить показания манометра (избыточное давление) в собственно давление газа или пара на стенки (абсолютное давление).
Принимаются следующие обозначения:
ра (или просто р) - абсолютное давление, в таблицах выражается обычно в килопаскалях (кПа) или мегапаскалях (МПа), а иногда в барах (бар);
ри - избыточное давление (по манометру), причем это давление на шкалах манометров принято выражать в старой системе единиц, т.е. в кГс/см2 (килограмм-сила на квадратный сантиметр),
В - барометрическое, или атмосферное давление, измеряемое по барометру, отградуированному обычно в мм рт.ст.
Вычисление абсолютного давления производится по формуле
ра = ри + В . (1-1)
Чтобы воспользоваться этой формулой, надо уметь выразить кГс/см2 и мм рт.ст. в кПа или МПа. В приближенных расчетах (прикидках) при невысоких давлениях можно (с целью упростить и ускорить расчет) принять, что
1 кГс/см2 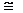 1 бар = 100кПа = 0,1 МПа,
1 бар = 100кПа = 0,1 МПа,
В 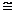 1 бар = 100 кПа = 0,1 МПа.
1 бар = 100 кПа = 0,1 МПа.
Температура
Как уже отмечалось, под термодинамическим равновесием понимается состояние покоя всех частей равновесной термодинамической системы. Причем, для термодинамического равновесия недостаточно, чтобы выполнялись условия только механического равновесия. Как показывает опыт, обобщенный т.н. нулевым законом термодинамики, равновесное состояние термодинамической системы достигается только при необходимом дополнительном условии - равенстве температур каждой из частей системы. А если система не изолирована от внешней среды, то для термического равновесия необходимо также и равенство температур системы и среды.
Шкала температур, показывающая, какая температура и на сколько выше, исторически была определена выбором термометрических тел, свойства которых, например, удельный объем или электрическое сопротивление монотонно изменяются с изменением температуры. Температурной шкалой, не зависящей от природы термометрического тела, является термодинамическая шкала температур. Абсолютная термодинамическая шкала температур выражается в кельвинах и обозначаемая через Т. Соотношение между нею и стоградусной шкалой, обозначаемой через t и измеряемой в 0С, имеет вид
T = t + 273,15.
Термодинамическая шкала температур в кельвинах является и абсолютной, поскольку в силу т.н. третьего закона термодинамики равновесные системы при Т = 0 должны находиться в состоянии, практически недостижимом.
Удельная внутренняя энергия
Если внутренняя энергия системы обозначается через U, кДж, а масса через m, кг, то удельная внутренняя энергия равна
u = U/m, кДж/кг.
Существенно, что для технических расчетов термодинамических процессов нужно знать и вводить в расчет или определять исключительно разность внутренних энергий начала и конца процесса, т.е. 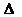 u или
u или 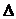 U.
U.
ТЕРМОДИНАМИКИ
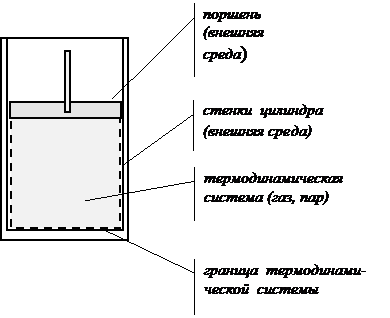
Термодинамическая система
Термодинамическое исследование начинается с выделения термодинамической системы - ограниченной области пространства, подлежащей рассмотрению, например, газового объема, массы кипящей жидкости или других объектов  . Все, что находится вне термодинамической системы и может взаимодействовать с нею, называют внешней, или окружающей средой. Термодинамическая система должна быть мысленно отделена от внешней среды границей термодинамической системы Назначение границы - фиксировать взаимодействие между термодинамической системой и внешней средой, а именно, вести учет потоков энергии, поступающих в систему (или выходящих из нее) и изменяющих энергию, аккумулируемую внутри системы.
. Все, что находится вне термодинамической системы и может взаимодействовать с нею, называют внешней, или окружающей средой. Термодинамическая система должна быть мысленно отделена от внешней среды границей термодинамической системы Назначение границы - фиксировать взаимодействие между термодинамической системой и внешней средой, а именно, вести учет потоков энергии, поступающих в систему (или выходящих из нее) и изменяющих энергию, аккумулируемую внутри системы.
 .
.
Рис.1-1.Простейшая термодинамическая система (закрытая)
Если граница непроницаема для массы вещества, то границу и соответственно термодинамическую систему называют закрытой. В противном случае мы имеем открытую границу и открытую термодинамическую систему. Например, фреон, циркулирующий в бытовом холодильнике, рассматривается как закрытая система, если пренебречь мизерными утечками фреона через стенки холодильной машины. Напротив, внутренние полости теплообменного аппарата, турбины или компрессора, через которые протекает рабочее тело и которые имеют входное и выходное отверстия, служат примером открытых систем. Нашей конечной целью является анализ, в основном, открытых систем.
Если через границу закрытой термодинамической системы переносится энергия только в форме работы сил, то такая система называется адиабатической, или адиабатно изолированной. Иначе, адиабатной называют систему без теплообмена. Турбины, компрессоры, воздуходувки – адиабатные системы.. Наконец, если граница непроницаема и для массы вещества, и для энергии в любой форме, то мы имеем изолированную термодинамическую систему.
Термодинамический процесс
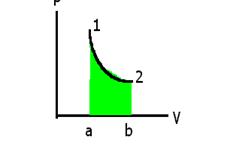 Термодинамическая система совершает работу L или воспринимает теплоприток Q только тогда, когда совершает термодинамический процесс. Процесс состоит из последовательности термодинамических состояний системы.
Термодинамическая система совершает работу L или воспринимает теплоприток Q только тогда, когда совершает термодинамический процесс. Процесс состоит из последовательности термодинамических состояний системы.
Рис.1-2. Изображение равновесного процесса 1-2 в рV-диаграмме. Площадь под кривой процесса выражает работу сил давления, представленную формулой (1-5).
В ОТКРЫТЫХ СИСТЕМАХ
Основными объектами термодинамических расчетов являются процессы в открытых системах – турбинах, компрессорах, теплообменниках, устройства для редуцирования давления. Процессы в турбинах и компрессорах являются практически равновесными адиабатными (изоэнтропными), в проточных теплообменниках – изобарными (за небольшими исключениями), в редукционных устройствах (редукционные установки в котельных, регулирующие вентили на холодильных машинах) – адиабатным дросселированием. Соответственно мы ограничимся рассмотрением трех названных видов процессов: изобарного (р=const), изоэнтропного (s=const) и адиабатного дросселирования..
При расчете открытых систем разного назначения используют энергетический баланс в виде равенств:
q = h 2 - h1 + lТЕХН (1-7а)
dlТЕХН= - v dp, lТЕХН= - 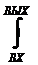 v dp. (1-9)
v dp. (1-9)
dq = T ds, q = 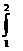 T ds (1-10)
T ds (1-10)
Изобарные процессы
Изобарные процессы совершаются в проточных теплообменниках. Следовательно, практический интерес представляет расчет теплопритока изобарного процесса.
В открытых стандартных системах, каковыми являются проточные теплообменники, техническая работа потоком рабочего тела не совершается. Действительно, из равенства (1-9) следует, что при dp=0 имеем lТЕХН=0. Соответственно из энергетического баланса (1-7а) следует формула теплового баланса, используемая для вычисления удельного теплопритока к теплообменникам:
q = h2 - h1, Q = Gq, (1-11)
где G – поток теплоносителя (кг). Значения удельных энтальпий определяют по известным параметрам теплоносителя на входе и выходе из аппарата.
Можно воспользоваться также таблицами изобарной теплоемкости сР см. п. 7.5):
q = сР (t2) t2 – cР(t1) t1.
Изоэнтропные процессы
Cтационарные процессы, протекающие в паровых турбинах или в компрессорах, практически являются равновесными адиабатами (q=0), то есть изоэнтропами. Поэтому для них энергетический баланс (1-7а) принимает частный вид, позволяющий вычислить удельную техническую работу:
lТЕХН = h1 - h2 . (1-12)
По этой формуле вычисляют техническую работу турбин и компрессоров, если известны параметры рабочего тела (хладагента) на входе и выходе из машины.
Адиабатное дросселирование
Дросселирование – это продавливание потока рабочего тела через узкое отверстие или длинный капилляр. Техническая работа потока при дросселировании равна нулю по определению (стенки аппарата неподвижны!): lТЕХН = 0. Притом обычно аппараты осуществляют дросселирование адиабатно, то есть без теплообмена, при q=0. Так что в этом случае энергетический баланс (1-7а) принимает вид
h1 = h2 , (1-13)
указывающий, что после протекания через адиабатно дросселирующие устройства рабочее тело восстанавливает свою энтальпию.
ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Процесс дросселирования
Если поток вещества проходит через препятствие - узкое отверстие, регулируемое или нерегулируемое, или через длинный тонкий капилляр (капиллярная трубка в бытовом холодильнике), то давление после препятствия падает. Давление пара понижают дросселированием в редукционных и редукционно-охладительных устройствах (РУ,РОУ) в собственных котельных предприятий, чтобы в технологические цеха к аппаратам поступал безопасный по давлению пар. Что происходит при дросселировании с температурой пара, зависит от области состояния, в которой находится дросселируемый пар, и определяется уравнением первого закона термодинамики для открытой системы (1-7а):
q = hвых- hвх+ lтехн.
При адиабатном дросселировании поток не совершает никакой технической работы и не вступает в теплообмен, так что
lтехн= q = 0.
Отсюда следует, что при адиабатном дросселировании значения энтальпии потока на входе и выходе из дросселирующего устройства равны(см.также формулу (1- 13)):
hвх = hвых.
Полученное условие адиабатного дросселирования позволяет определить, в какой области состояний рабочего тела и в какой степени его температура изменяется при адиабатном дросселировании. Для этого надо на диаграмме состояния проследить направление линий изоэнтальп h = const. Легко можно увидеть, что в области влажного пара температура на изоэнтальпах резко падает с понижением давления. Это свойство области влажного пара используют в парокомпрессионных холодильных машинах, пропуская поток влажного пара хладагента через дроссельное устройство - терморегулирующий вентиль в промышленных холодильных машинах или через капиллярную трубку в бытовых холодильниках - и тем самым понижая вместе с понижением давления потока хладагента и его температуру, например, от 200С до -100С.
Можно также заметить, что в другой области состояний - области перегретого пара изоэнтальпы направлены почти параллельно изотермам. Следовательно, здесь понижение температуры пара при дросселировании незначительно. Поэтому дросселирование, например, сухого насыщенного пара после котла с целью снизить давление до безопасного приводит лишь к незначительному понижению температуры (если редукционное устройство не осуществляет дополнительно впрыск воды для охлаждения пара).
Свойства идеальных газов
Термодинамические свойства газов, то есть соотношение между их параметрами и функциями в равновесном состоянии зависят в общем случае от уровня температур и давлений. При не слишком высоких давлениях их плотности малы (удельные объемы велики), поэтому их термодинамические свойства приближаются к свойствам идеальных газов.
Закон Джоуля
Вторая отличительная особенность идеальных газов - это то, что их энтальпия и внутренняя энергия зависят только от температуры (закон Джоуля). Так, если в общем случае удельная энтальпия определяется как функция двух параметров, h = h(t, p), то согласно закону Джоуля в случае идеального газа энтальпия не зависит от изменения давления:
hид= h(t), uид= u(t). (1-18)
7.5. Теплоемкости сР и сV газов
Важной характеристикой термодинамических свойств веществ, особенно газов, является их т е п л о е м к о с т ь. Теплоемкостью называют способность тел воспринимать определенную величину теплопритока при изменении температуры тела на один градус.
Теплоемкость единицы массы тела (1 кг) обозначают буквой с и измеряют в кДж/кг/К, или, что равносильно, в кДж/кг / оС.
Различают теплоемкости - среднюю в интервале температур t1...t2
и истинную в окрестностях температуры t:
c12 = q / (t2- t1), сt = dq / dt. (1-19)
Эти теплоемкости связаны очевидным соотношением
с12(t2- t1) =  ct dt .
ct dt .
Особенностью, отличающей газы от твердых или жидких тел, является способность газов при изменении температуры существенно изменять объем. Поэтому величина теплоемкости зависит от вида процесса. Важную роль в расчетах играют теплоемкости изобарного и изохорного процессов.
Чтобы различать теплоемкости этих двух процессов - изобарного и изохорного, их обозначают различными нижними индексами: cP и cV.
Можно показать, что теплоемкости ср и сv с связаны с энтальпией и соответственно внутренней энергией газов. Действительно, первый закон термодинамики для равновесных процессов выражается любым из двух равенств -
dq = dh - v dp, или dq = du + p dv. (1-20)
При p = const первое из этих равенств принимает вид
dqp= dh, или qp= h2- h1 ,
откуда с учетом формулы (1-19) выявляется прямая взаимозависимость между энтальпией и изобарной теплоемкостью:
dh = cp dt, (1-21)
h2- h1= (cp)12 (t2 - t1). (1-22)
Аналогично, при v = const имеем
dqv= du, qv = u2 - u1
du = cvdt,
u2 - u1 = (cv)12 (t2 - t1). (1-23)
Полученные равенства, действительно, устанавливают взаимозависимость между изменением ср и h и между изменением сv и u.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ ПО РАЗДЕЛУ 1
1. Какие формы переноса энергии, кроме работы сил, существуют в природе и рассматриваются термодинамикой?
2. В каких единицах измеряют энергию, переносимую в форме работы сил, в частности, электроэнергию? То же - переносимую при теплообмене? Какие единицы этих видов переноса энергии установлены в СИ?
3. Почему рыночная цена единицы электрической энергии, а в общем случае - работы сил, выше, чем цена такой же единицы тепловой энергии?
4. В каких случаях и как можно определить по манометру температуру пара в паровом котле ? То же - в конденсаторе или испарителе холодильной машины?
5. Что означает и чему примерно равна величина КПД двигателей внутреннего сгорания на транспортных средствах и теплосиловых установок на паротурбинных или газотурбинных электростанциях?
ТЕСТ ПО РАЗДЕЛУ 1
Исключите (зачеркните) по одному неверному варианту в каждом из следующих суждений (верные ответы даны в конце пособия):
1. Величинами, которые перешли в термодинамику из механики, являются:
А- Давление р, Па. Б- Работа силы L, Дж. В- Температура t,0C.
2. Величинами, включаемыми в I закон термодинамики, являются:
А- Теплоприток (теплота процесса) Q. Б- Работа силы L. В- Энтропия S. Г- Внутренняя энергия U.
3. Давление в 1 МПа можно выразить как
А- 103 кПа. Б- 10,2 кГс/см 2. В- 750 мм рт.ст.
4. 1 МДж равен
А- 3,6 кВт.ч. Б- 1/3,6 кВт.ч. В- 4,19.103 ккал.
5. Водяной пар при 0,102 МПа и 1000С может представлять собой
А- перегретый пар. Б- влажный пар. В- сухой насыщенный пар.
* * *
ТЕПЛОПРОВОДНОСТЬ
Тепловой поток, передаваемый в единицу времени через произвольную поверхность, обозначается Q, измеряется Вт=Дж/с.
Интенсивность теплопереноса теплоты характеризуется плотностью теплового потока
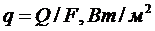 2.1
2.1
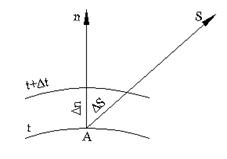
Температура есть мера нагретости тела. Поверхность, во всех точках которой температура одинакова, называется изотермической. Рассмотрим две изотермы с температурами t и t + Δt (рис.2.1) Интенсивность изменения температуры по различным направлениям неодинакова. Температура быстрее всего изменяется в направлении, перпендикулярном изотермической поверхности. Вектор, направленный по нормали к изотермической поверхности в сторону увеличения температуры и численно равный производной от температуры по этому направлению называется градиентом температуры – grad t.
За положительное направление градиента принимается направление возрастания температур.
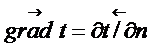 2.2.
2.2.
Рис 2.1 Интенсивность изменения температуры
Для измерения температуры наиболее широко используют шкалу Цельсия, в которой за нулевую температуру принята точка замерзания воды при барометрическом давлении 760 мм рт ст. В ряде случаев используют шкалу Кельвина, при которой температура ноль градусов соответствует абсолютному нулю.
Т = t0C + 273,15
Совокупность значений температуры во всех точках тела в данный момент времени называется температурным полем. Если температура изменяется во времени, то температурное поле нестационарно t = ƒ (τ). Если температура во всех точках тела не изменяется с течением времени, то поле стационарное. Температура является функцией координат и соответственно поле бывает трехмерным, двухмерным и одномерным.
КОНВЕКТИВНЫЙ ТЕПЛООБМЕН (ТЕПЛООТДАЧА)
Процесс теплообмена между поверхностью твердого тела и жидкостью, имеющих разные температуры, называется теплоотдачей. Теплоотдача обычно сопровождается теплопроводностью. Совместный процесс конвекции и теплопроводности называется конвективной теплоотдачей.
Согласно закону Ньютона-Рихмана тепловой поток в процессе теплоотдачи пропорционален коэффициенту теплоотдачи, площади поверхности теплообмена и разности температур поверхности тела и жидкости.
Q = 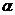 (tс – tж)F , 2.17
(tс – tж)F , 2.17
В расчетах разность температур tс – tж берут по абсолютной величине. Коэффициент теплоотдачи α Вт/(м2·К) характеризует интенсивность процесса теплоотдачи и зависит от большого числа факторов:
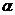 = ƒ ( tж, t ст, d, λ, ν, ω, ℓ, ġ, β Х…….) 2.18
= ƒ ( tж, t ст, d, λ, ν, ω, ℓ, ġ, β Х…….) 2.18
где : tж-температура жидкости,0С ; tст – температура стенки, 0С; d –диаметр трубы, м;
λ – теплопроводность жидкости, Вт/ ( м К ): ω –скорость течения жидкости, м/с; ℓ – определяющий размер ( для труб – диаметр ), м ; g – ускорение свободного падения, 9,8 м/с2 ;
β – коэффициент объемного расширения, 1/К ; Х – характер течения жидкости; ν – кинематический коэффициент вязкости, м2/с.
Из формулы 2.18 видно, что коэффициент теплоотдачи определить сложно, т.к. он зависит от большого числа переменных.
Существует два способа решения задач конвективного теплообмена: аналитический и с применением теории подобия.
При аналитическом решении задач конвективного теплообмена составляются дифференциальные уравнения, учитывающие тепловые и динамические явления в рассматриваемом процессе. Вывод таких уравнений рассматривается в специальной литературе.
Конвективный теплообмен в несжимаемой однофазной среде описывается следующими уравнениями.
Уравнение теплоотдачи:
α = -( λ/θ ) ( ∂t / ∂n )n=0, где θ = t – t0. 2.19
Дифференциальное уравнение теплопроводности (сплошности) имеет вид:
∂t /∂τ = а 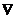 2t = [∂ 2t / ∂x2 +∂2t / ∂y2 + ∂2t / ∂z2 ] λ /с ρ 2.20
2t = [∂ 2t / ∂x2 +∂2t / ∂y2 + ∂2t / ∂z2 ] λ /с ρ 2.20
где: ∂t /∂τ – температурное поле исследуемого объекта, которое зависит от изменения температуры по осям , т.е. от оператора Лапласа,
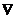 2t = ∂2t /∂x2 + ∂2t / ∂y2 + ∂2t /∂ z2, 2.21
2t = ∂2t /∂x2 + ∂2t / ∂y2 + ∂2t /∂ z2, 2.21
и от теплофизических свойств: коэффициента температуропроводности – а (м2/с), удельной теплоемкости – с (кДж/(кг К) и плотности ρ (кг/м3)
Дифференциальное уравнение движения:
∂ω/ ∂τ = gβ 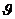 – 1/ρ (
– 1/ρ ( 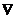 ρ) + ν
ρ) + ν 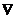 2ω. 2.22
2ω. 2.22
Дифференциальное уравнение сплошности: 
∂ωх / ∂х + ∂ωу / ∂у + ∂ωz / ∂z = 0 или div = 0 2.23
Приведенные дифференциальные уравнения конвективного теплообмена 2.19 – 2.22 описывают бесчисленное множество процессов. Чтобы решить конкретную задачу, к приведенным уравнениям следует присоединить условия однозначности. Условия однозначности дают математическое описание частных случаев. Условия однозначности состоят:
1)из геометрических условий, характеризующих форму и размеры тела или системы, в которой протекает процесс;
2) физических условий, характеризующих физические свойства среды;
3) граничных условий, определяющих особенности протекания процесса на границах жидкой среды;
4) временных или начальных условий, характеризующих особенности процесса в начальный момент времени; для стационарных процессов эти условия отпадают.
Решение приведенных систем дифференциальных уравнений и условий однозначности с большим количеством переменных получается сложным. Поэтому большое значение приобретает экспериментальный путь исследования и применение теории подобия.
В основе теории подобия лежат три теоремы.
Первая терема подобия: у подобных явлений числа подобия численно одинаковы.
Вторая теорема подобия: если физическое явление описывается системой дифференциальных уравнений, то всегда существует возможность представить их в виде уравнений подобия.
Третья теорема подобия: подобны те явления, условия однозначности которых подобны, и числа подобия, составленные из условий однозначности, численно одинаковы. 
Сущность теории подобия состоит в том, что размерные физические величины, влияющие на конвективный теплообмен, объединяются в безразмерные комплексы, причем так, что число комплексов меньше числа величин, из которых составлены эти комплексы. Комплексам или числам подобия присваиваются имена ученых, внесших большой вклад в исследование процессов теплопереноса и гидродинамики
Полученные безразмерные комплексы рассматриваются как новые переменные. Они отражают не только влияние одиночных факторов, но и их совокупности, что упрощает описание исследуемого процесса. Теория подобия является теоретической базой эксперимента, облегчает анализ процессов. Рассмотрим применение теории подобия для исследования конвективных процессов теплоотдачи.
Из формулы 2.17 видно, интенсивность конвективного теплообмена характеризуется коэффициентом теплоотдачи, который зависит, в частности, от определяющего размера, площади теплообменной поверхности, температуропроводности, теплопроводности, температурного напора, скорости движения жидкости, коэффициента кинематической вязкости и т. д.
Из этих величин составлены безразмерные комплексы – числа подобия (критерии подобия).
число Нуссельта Nu = αℓ / λ 2.24
число Рейнольдса Re = ωℓ / ν 2.25
число Грасгофа Gr = g β Δt ℓ3/ ν2 2.26
число Прандтля Рr = ν /а 2.27
Число Нуссельта – определяемое число, т.к. в него входит искомый коэффициент теплоотдачи. Числа Рейнольдса, Грасгофа, Прандтля – определяющие. Они состоят из величин, известных до решения задачи. В общем виде
Nu= ƒ ( Rе, Gr, Рr ) 2.28
Для решения задач приведенное уравнение записывается в степенном виде:
Nu = c Rеm Grn Рrr 2.29
Различают естественное (свободное) и вынужденное течение жидкости.
Естественная конвекция возникает за счет разности плотностей холодных и горячих частиц жидкости около поверхности нагрева. Интенсивность теплового расширения характеризуется температурным коэффициентом объемного расширения β Для газов, которые в большинстве случаев можно считать идеальными, коэффициент объемного расширения определяется равенством
β = 1/Т 2.30
При естественной конвекции уравнение 2.28 упрощается:
Nu= с ( Gr, Рr )n 2.31
Вынужденная конвекция создается внешним источником (насосом, вентилятором). Для вынужденной конвекции уравнение 2.28 имеет вид:
Nu = с Rеm Prn 2.32
Задачей эксперимента является определение конкретного вида функциональной связи в уравнении подобия, т.е. следует найти числовые значения коэффициентов, показателей степеней и т.д.
Определив число Нуссельта, можно рассчитать искомый коэффициент теплоотдачи:
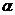 = Nu ℓ /λ 2.33
= Nu ℓ /λ 2.33
Как показали экспериментальные исследования, режим течения определяется скоростью потока.
О. Рейнольдс опытным путем установил, что при движении жидкости встречаются два вида потока, подчиняющимся различным законам. В одном виде потока все частицы движутся только по параллельным траекториям и движение длительно совпадает с направлением всего потока. Жидкость движется спокойно, без пульсаций. Такое движение названо ламинарным. При ламинарном течении в трубе число Рейнольдса менее 2300.
Во втором типе потока происходит непрерывное перемешивание всех слоев жидкости. Поток представляет беспорядочную массу хаотически движущихся частиц. Такой тип потока называется турбулентным. При турбулентном течении число Рейнольдса более 104.
При числах Рейнольдса более 2000, но менее 1.104 движение жидкости нестабильное. Режим течения называется переходным.
Теоретическое исследование задач конвективного теплообмена основано на теории пограничного слоя, разработанной Л. Прандтлем.
Введены понятия теплового и динамического пограничных слоев.
Если температуры стенки и жидкости неодинаковы, то вблизи стенки образуется тепловой пограничный слой, в котором происходит изменение температуры. Вне пограничного слоя температура жидкости одинакова и равна температуре потока.
Тонкий пограничный слой жидкости вблизи поверхности, в котором происходит изменение скорости от значения скорости невозмущенного потока вдали от стенки до нуля непосредственно на стенке, называется динамическим пограничным слоем.
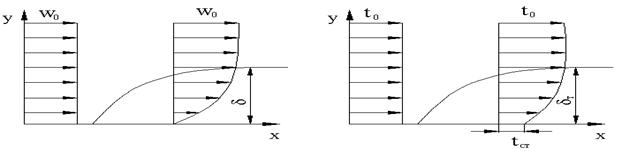
Рис.2.4 Распределение температуры и скорости в тепловом
и динамическом пограничном слое
С увеличением вязкости толщина динамического слоя увеличивается, с увеличением скорости потока толщина динамического слоя уменьшается. Течение в динамическом слое может быть как ламинарным, так и турбулентным и определяется числом Рейнольдса.
Толщины теплового и пограничного слоев могут не совпадать. Соотношение толщин динамического и теплового пограничных слоев определяется безразмерным числом Прандтля. Для вязких жидкостей, например, масел, Рr>1. Для вязких жидкостей, например, масел толщина динамического пограничного слоя больше толщины теплового пограничного слоя. Для газов Рr ≈ 1и толщины слоев приблизительно одинаковы. Для жидких металлов Рr < 1, толщина теплового пограничного слоя больше толщины динамического пограничного слоя.
Если движение внутри теплового пограничного слоя ламинарное, то теплообмен осуществляется теплопроводностью. С увеличением скорости в пограничном слое и появлением турбулентности следует учитывать интенсивность перемешивания жидкости.
В процессе продольного обтекания какого-либо тела безграничным потоком жидкости с постоянной скоростью течения в непосредственной близости от поверхности тела скорость течения должна падать до нуля.
При решении задач конвективного теплообмена следует обращать внимание на то, какая температура для данного уравнения подобия принимается за определяющую, т.к. физические параметры жидкостей и газов изменяются с изменением температуры.
Для простейших случаев, когда температура потока изменяется в небольших пределах, среднюю температуру жидкости можно определить как среднеарифметическую у входа в канал t1 и выхода из канала t2: tж = 0,5 (t1 – t2).
Для более точных расчетов пользуются формулой
tж = 0, 5 ( t1 – t
