Свойства несобственных интегралов с бесконечными пределами интегрирования.
1) Если  то для несобственного интеграла справедлива формула Ньютона-Лейбница
то для несобственного интеграла справедлива формула Ньютона-Лейбница
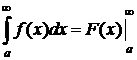
Кроме этого 
2) Свойство линейности сохраняется и для несобственных интегралов.
3) Запишем несобственный интеграл в виде

Для того, чтобы несобственный интеграл сходился необходимо и достаточно, чтобы
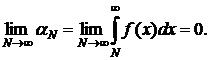
Несобственные интегралы вычисляются достаточно редко, гораздо чаще нас интересует факт их сходимости или расходимости, для этого достаточно исследовать поведение остатка 
Несобственные интегралы с бесконечными пределами интегрирования от неотрицательных функций. Доказать признаки сравнения. Эталонные функции. Примеры.
Пусть подынтегральная функция  тогда
тогда  является возрастающей функцией.
является возрастающей функцией.
Таким образом у функции  имеется две возможности:
имеется две возможности:
1) 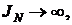 т.е. возрастает неограниченно;
т.е. возрастает неограниченно;
2) 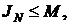 т.е. ограничена сверху.
т.е. ограничена сверху.
В этом случае по теореме о пределе монотонной переменной мы имеем, что существует предел  и он не превосходит M, т.е.
и он не превосходит M, т.е. 
Т.е. в этом случае несобственный интеграл сходится.
Таким образом для неотрицательных функций исключается возможность отсутствия пределов у  . Это позволяет построить хорошую теорию исследования этих интегралов. Основной способ исследования на сходимость несобственных интегралов заключается в сравнении их с уже известными интегралами, иначе говоря с интегралами от так называемых эталонных функций.
. Это позволяет построить хорошую теорию исследования этих интегралов. Основной способ исследования на сходимость несобственных интегралов заключается в сравнении их с уже известными интегралами, иначе говоря с интегралами от так называемых эталонных функций.
Теорема 1. (признак сравнения в обычной форме).
Пусть функции 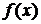 и
и  не отрицательны интегрируемые и справедливо соотношение
не отрицательны интегрируемые и справедливо соотношение
 для
для 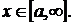
Тогда если 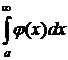 сходится, то сходится
сходится, то сходится 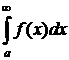 . Если
. Если 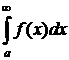 расходится, то
расходится, то 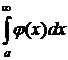 тоже расходится.
тоже расходится.

Доказательство.
Проинтегрируем исходное неравенство в пределах от a до N, получим
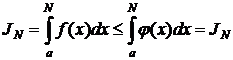
Если  то JN ограничена сверху,
то JN ограничена сверху, 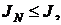 а значит по теореме о пределе монотонной переменной
а значит по теореме о пределе монотонной переменной 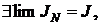 т.е. интеграл сходится.
т.е. интеграл сходится.
Обратное утверждение доказывается совершенно аналогично.
Гораздо чаще, чем теорема 1, на практике применяется теорема 2 (признак сравнения в предельной форме)
Пусть функции 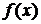 и
и  неотрицательны и интегрируемые и пусть
неотрицательны и интегрируемые и пусть
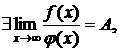 при этом
при этом 
Тогда 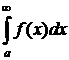 и
и 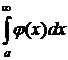 сходятся и расходятся одновременно.
сходятся и расходятся одновременно.
Доказательство.
По теореме о связи последовательности, имеющей предел с бесконечно малой, мы имеем 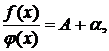 где
где 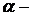 БМ. Иначе говоря, для достаточно больших N справедливо соотношение
БМ. Иначе говоря, для достаточно больших N справедливо соотношение
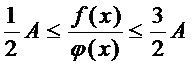

А теперь воспользуемся теоремой 1.
Для определения теорем сравнения нужно иметь набор эталонных функций, т.е. функции, о которых заранее известно сходятся или расходятся интегралы от них. В качестве таких функций чаще всего выбираются такие степенные функции
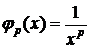


32.Дать определения абсолютной и условной сходимости несобственных интегралов. Доказать теорему о связи сходимости к абсолютной сходимости. Примеры.
Если подынтегральная функция имеет произвольный знак, то 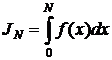 - немонотонная функция и поэтому вся предыдущая теория не годится. Однако, имеется один частный, но важный случай, когда можно сказать что-то определенное и об этих интегралах. Это случай абсолютной сходимости.
- немонотонная функция и поэтому вся предыдущая теория не годится. Однако, имеется один частный, но важный случай, когда можно сказать что-то определенное и об этих интегралах. Это случай абсолютной сходимости.
Говорят, что 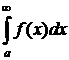 сходится абсолютно, если сходится
сходится абсолютно, если сходится 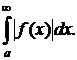
Теорема 3. Если интеграл сходится абсолютно, то он сходится.
Однако, возможна ситуация, когда интеграл от модуля расходится, а исходный интеграл сходится. В этом случае
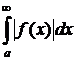 - расходится;
- расходится; 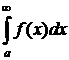 - сходится условно.
- сходится условно.
Дать определение несобственных интегралов от неограниченных функций. Сформулировать их свойства, теоремы сравнения для них. Привести эталонные функции. Примеры.
Пусть функция f(x) определена на [a;b) и 

В этом случае опять нельзя определить интеграл обычным образом с помощью интегральных сумм, т.к. в последнем слагаемом 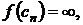 поэтому опять обрезают хвост и определяем несобственный интеграл от неограниченной функции, как предел собственных интегралов при
поэтому опять обрезают хвост и определяем несобственный интеграл от неограниченной функции, как предел собственных интегралов при  , т.е.
, т.е.

Если этот предел существует и конечен, то несобственный интеграл сходится. Если же он не существует или равен 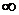 , то несобственный интеграл расходится.
, то несобственный интеграл расходится.
Все свойства несобственных интегралов 1-ого рода сохраняются и для несобственных интегралов 2-ого рода. Более того, если существует  то сохраняется и формула Ньютона-Лейбница
то сохраняется и формула Ньютона-Лейбница 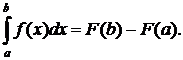
Замечание. Если точка разрыва 2-ого рода подынтегральной функции находится внутри области интегрирования, то мы вырезаем ее окрестность и получаем 2 несобственных интеграла 2-ого рода, при этом окрестности вырезаются вообще говоря не симметрично.
Для несобственных интегралов 2-ого рода от положительных функций также справедливы теоремы сравнения. Однако, в качестве эталонных функций выбираются функции 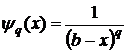
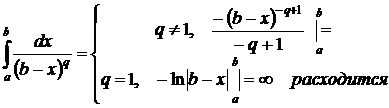
Рассказать о вычислении двойного интеграла в декартовых, полярных координатах и о перемене порядка интегрирования. Примеры.
Вычисление двойного интеграла сводится к вычислению 2-х определенных интегралов. Рассмотрим как это делается. Требуется вычислить 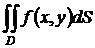
Область D называется правильной относительно оси OX, если всякая вертикальная прямая пересекает ее не более, чем в 2-х точках, называемых точками входа и выхода.
Аналогично, область называется правильной относительно оси OY, если всякая горизонтальная прямая пересекает эту область в 2-х точках.
Всякая неправильная область может быть разбита на конечное число правильных областей, поэтому будем считать, что область D – правильная.
Пусть сначала подынтегральная функция f(x,y) неотрицательна, тогда ее можно трактовать, как плотность функции  и двойной интеграл представляет собой массу пластины.
и двойной интеграл представляет собой массу пластины.
Найдем сейчас эту массу другим способом: разобьем область D на вертикальные стержни, а затем каждый стержень на кусочки.
Элемент площади 
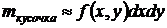
Масса стержня 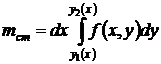
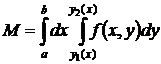
Итак, мы получили, что 
Эта формула справедлива и в тех случаях, когда функция f(x,y) имеет произвольный знак.
