Замена переменной в определенном интеграле.

Если функции f(x) и 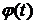непрерывны, то

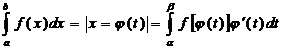
Здесь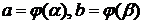

Точнее теорема о замене переменной формулируется так:

1. Если функция f(x) непрерывна на
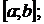
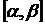2. переходит в 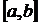, т.е. интервал 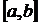является множеством значений функции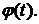
3. Функция 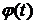непрерывно дифференцируема на 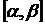и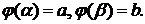

Иными словами, чтобы функция g(x) или монотонно возрастала или монотонно убывала на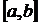

Интегрирование по частям в определенном интеграле.

Формула интегрирования по частям имеет вид

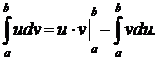
29.Вывести формулы приближенного вычисления определенных интегралов (формулы прямоугольников, трапеция, Симпсона).

Приближенное вычисление определенных интегралов.

Идея всех методов заключается в замене криволинейной трапеции другими фигурами, площади которых легко вычисляются. Мы рассмотрим 3 таких формулы:

Формула прямоугольников.

Разбиваем область интегрирования на n-равных частей

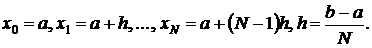
Затем заменяем площадь каждой маленькой криволинейной трапеции площадью прямоугольника.

Получаем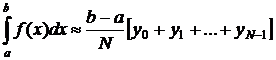

Можно записать эту же формулу, только брать в качестве высот правые концы, тогда

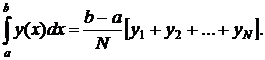
Эта формула не очень точна и годится для приближенной прикидки. Фактически здесь мы заменяем график подынтегральной функции некоторой ступенчатой кривой.

2) Формула трапеций.

Естественно, что если заменять график подынтегральной функции некоторой вписанной ломаной, то точность приближенной формулы повышается.

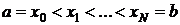
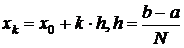
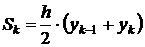
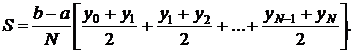
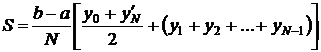
Число N выбирается произвольно. Чем больше N, тем выше точность вычисления. Если у нас задана точность 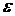, с которой нужно вычислить заданный интеграл, то можно поступать следующим образом.

Вычисляем интеграл дважды

Если 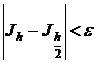, то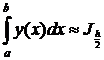

Если превышает, то мы снова увеличиваем в 2 раза число интервалов разбиений.

Наиболее точной из этих 3-х формул является формула парабол (формула Симпсона).

Ее идея состоит в замене двух соседних верхних крышек маленьких криволинейных трапеций куском параболы 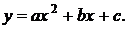Разобьем теперь 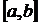на четное число частей.

Справедлива следующая лемма

Если криволинейная трапеция ограничена сверху параболой 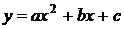, осью OX и двумя ординатами с расстояниями между ними 2h, то площадь этой трапеции

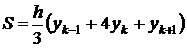
Доказательство.

Выберем систему координат следующим образом

Тогда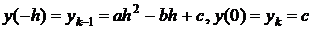

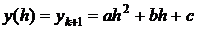
С другой стороны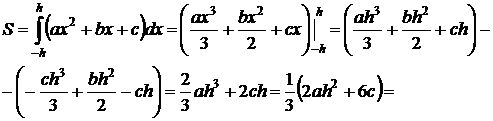

Попытаемся получить такое же выражение, не зная интегральных выражений y(-h), y(0), y(h).

Получим

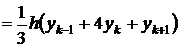
Лемма доказана.

Складывая площади всех маленьких трапеций получаем

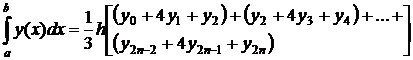
30. Дать определения и привести основные свойства несобственных интегралов с бесконечными пределами интегрирования. Примеры.

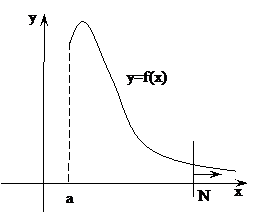
для линии y=f(x) ось OX является асимптотой.

.

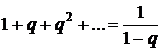Для вычисления этой площади нужно вычислить 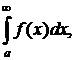его нельзя определить через интегральные суммы, как мы делали ранее, т.к. последний интервал всегда будет иметь бесконечную длину, поэтому мы поступим следующим образом:

Сначала обрежем бесконечный хвост, т.е. рассмотрим

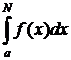- этот интеграл определяется обычно через предел интегральных сумм, а затем устремим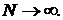

Если 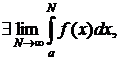то он и будет называться несобственным интегралом от функции f(x). Итак, процедура определения несобственного интеграла содержит 2 предельных перехода:

1. предел интегральных сумм;

2. предел определенного интеграла, когда его верхняя граница стремится к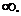

Если предел существует и конечен, то говорят, что несобственный интеграл сходится.

Если этот предел не существует или равен бесконечности, то говорят, что несобственный интеграл расходится.