Невесомый стержень с шарнирами

Реакция N невесомого стержня направлена вдоль стержня. Обычно реакция Nизображается от тела по стержню, в предположении, что в равновесии стержень растянут.

4. Неподвижный цилиндрический шарнирилиподшипник

Реакция R_A цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси вращения, т. е. в плоскости Аху. Обычно ее раскладывают на две составляющие Х_А и Y_A по двум взаимно перпендикулярным направлениям.

Шарнирно-подвижная опора (опора на катках)

Реакция R проходит через ось шарнира и направлена перпендикулярно к опорной плоскости.

Жесткая заделка

Нахождение реакции жесткой заделки сводится к определению составляющих Х_А и Y_A препятствующих линейному перемещению балки в плоскости действия сил, и алгебраической величине момента m_A, препятствующего вращению балки под действием приложенных к ней сил.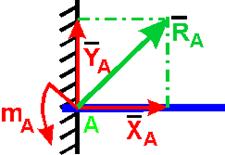

Возможные перемещения механической системы. Принцип возможных перемещений. Применения принципа возможных перемещений к решению задач статики.

Пример 1. Какую силу F надо приложить к желобу с грузом весом Р, чтобы удержать его в равновесии (рис.4)?

Рис.4

Решение.Эту задачу можно решить известными методами статики, составляя уравнения равновесия. Но при этом придется прежде отыскать усилия в стержнях. Принцип возможных перемещений позволяет найти силу F проще, с помощью общего уравнения статики.

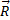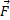Показываем активные силы и . Даем системе возможное перемещение, повернув стержень АО на угол 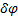(рис.66). Так как желоб совершит поступательное движение, то перемещения всех его точек будут одинаковы:

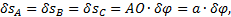
где a=AO=BD.

Составляем уравнение работ: 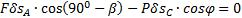. Угол .

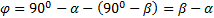Поэтому получим 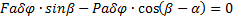. Отсюда .

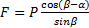Общее уравнение динамики.

По принципу Даламбера материальную систему, движущуюся под действием некоторых сил, можно рассматривать находящейся в равновесии, если ко всем точкам системы приложить их силы инерции. Значит можно воспользоваться и принципом возможных перемещений.

В уравнение работ (1) добавится еще сумма работ сил инерции точек на их возможных перемещениях:

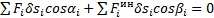. (3)

Или по принципу возможных скоростей (2):

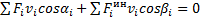(4)

Эти уравнения называют общим уравнением динамики. Оно позволяет решать большой класс задач на исследование движения довольно сложных материальных систем.

Уравнения (3) и (4) показывают, что в любой фиксированный момент времени сумма элементарных работ активных сил и сил инерции на любых виртуальных перемещениях равна нулю при условии, что на систему наложены идеальные и удерживающие связи.

Стоит подчеркнуть еще одно важное достоинство этого метода, общего уравнения динамики, – реакции связей (идеальных) исключаются при исследовании движения системы.

Иногда это уравнение можно использовать для исследования движения механических систем и в тех случаях, когда не все связи являются идеальными, например, когда имеются связи с трением. Для этого следует к активным силам добавить те составляющие реакций, которые обусловлены наличием сил трения.