Несобственный интеграл с бесконечным пределом (ами) интегрирования

Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: 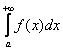. В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .

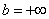Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: .

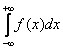Мы рассмотрим самый популярный случай 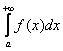. Техника работы с другими разновидностями – аналогична, и в конце параграфа будет ссылка на такие примеры.

Всегда ли существует несобственный интеграл 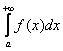? Нет, не всегда.Подынтегральная функция должна быть непрерывной на промежутке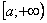

Справка: строго говоря, утверждение неверно: если есть разрывы функции, то в ряде случаев можно разбить полуинтервал на несколько частей и вычислить несколько несобственных интегралов. Для простоты здесь и далее я буду говорить, что несобственного интеграла не существует.

Изобразим на чертеже график подынтегральной функции . Типовой график и криволинейная трапеция для данного случая выглядит так:

Здесь всё хорошо, подынтегральная функция непрерывна на полуинтервале 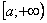, а, значит, несобственный интеграл существует. Обратите внимание, что криволинейная трапеция у нас – бесконечная (не ограниченная справа) фигура.
Несобственный интеграл 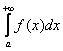численно равен площади заштрихованной фигуры, при этом возможны два случая:

1) Первое, мысль, которая приходит в голову: «раз фигура бесконечная, то 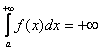», иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что, что несобственный интеграл расходится.

2) Но. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится.

В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.

А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл 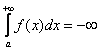(расходится) либо равен конечному отрицательному

числу.

15 Несобственные интегралы от неограниченных функций

Иногда такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: . Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке 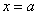, 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.

Если подынтегральной функции не существует в точке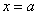

Сразу пример, чтобы было понятно: 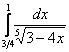. Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела 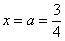, то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!

Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования. В этой связи проверим и верхний предел: 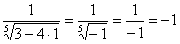. Здесь всё хорошо.

Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:

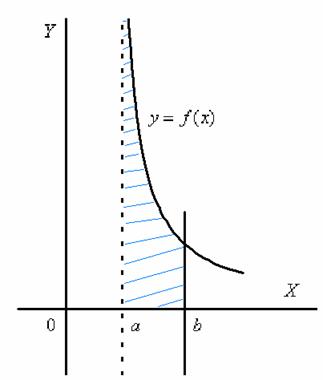
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).

Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значениюсправа.Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться кточке разрыва справа.

ФНП

1.Основные понятия.

Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.

Обычно функция нескольких переменных задается явным аналитическим способом. Например: z=3x+5y²,u=xy+z² и т.д.

Встречается также и неявное задание таких функций, например: z-2x-sinxy=0.

Упорядоченная пара чисел (x,y) может рассматриваться как точка на плоскости, т.е. Z есть функция точки (x,y).

Чтобы задать функцию z=f(x,y), надо не только указать правило нахождения z по заданным x и y, но и то множество (называемое областью задания функции) пар значений, которые могут принимать аргументы x и y.

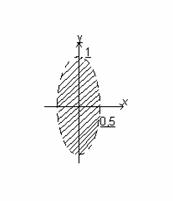
Например, функция z= 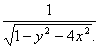задана только при 1-y 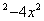>0, т.е. внутри эллипса y²+4x²<1 с полуосями, а=0,5 и в=1 не включая точки, лежащие на эллипсе.

Определение. Если каждой совокупности значений переменных x,y,z…t соответствует определенное значение переменной w, то w называется функцией независимых переменных x,y,z…t и записывается w=f(x,y,z…t).

Для функции трех переменных областью определения является упорядоченная тройка чисел (x,y,z), т.е. некоторая совокупность точек пространства. Область определения функции четырех и большего числа переменных не допускает простого геометрического истолкования.

Функции двух переменных допускают графическую иллюстрацию. Графиком функции z=f(x,y), заданной на некотором множестве D точек плоскости ХОУ, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежит D, а z=f(x,y). В наиболее простых случаях такой график представляет собой некоторую поверхность.

Например, графиком функции z=4-x²-y² является параболоид.

17 пространство Rⁿоткрытые, замкнутые связные

Определение 1. Упорядоченная совокупность из n действительных чисел 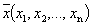называется n-мерной точкой.

Определение 2. Расстоянием между двумя n-мерными точками 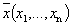называется величина

.

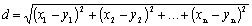Определение 3. Совокупность всех n-мерных точек с введенной на ней метрикой 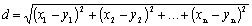называется n-мерным евклидовым (метрическим) пространством Rⁿ.

Пример 1. R². M(a,b) - точка из R², в линейном векторном

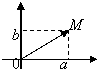пространстве Е² аналогично обозначается вектор 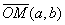. Между точками и векторами с одинаковыми координатами существует взаимно однозначное соответствие. Поэтому в дальнейшем мы будем обозначать их одинаково: .

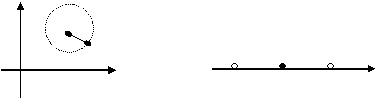
Пример 2.R¹. =а.

0 a

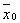Определение 4. -окрестностью точки в Rⁿ называется множество точек 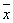, удовлетворяющих условию .

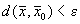Пример 3.R² R

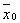
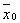e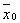

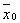-e +e

Определение 5. Множество А Rⁿ называется открытым, если любая точка входит в него вместе с некоторой окрестностью.

Определение 6.Множество B Rⁿ называется замкнутым, если оно является дополнением до некоторого открытого множества.

В - замкнутое ó Rⁿ \ B - открытое.

Пример 4. R¹.

-11

(-1,1) - открытое,

[-1,1] - замкнутое.

Открытые множества: (a,b), (-¥,a), (a,+¥), R, Æ.

Замкнутые множества: А=[a,b], R \ A, (-¥,a], [а,+¥) , R, Æ.

Пример 5. R².

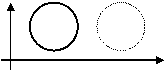Без границ – открытое множество,

с границами - замкнутое.

Определение 7. Отрезком в Rⁿ , соединяющим точк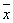и и , называется множество точек, удовлетворяющее условию .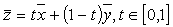

Определение 8. Множество А 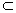Rⁿ называется выпуклым, если вместе с любыми двумя точками, входящими в него, оно содержит отрезок, их соединяющий.

Выпуклые множества. Невыпуклые множества.

Определение 9. Точка х Rⁿ называется угловой точкой множества А, если она не является внутренней ни для какого отрезка, целиком лежащего в А.

Угловые точки

Неугловые точки

Теорема. Пересечение конечного числа выпуклых множеств есть выпуклое множество.

Доказательство. Пусть А и В - выпуклые множества.

Докажем, что 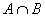- выпуклое множество.

Пусть х, у .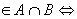

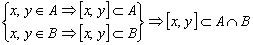Следовательно, 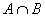- выпуклое множество.

Предел и непрерывность ФНП

Непрерывность функции нескольких переменных.

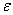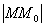Определение. Число А называется пределом функции f(M), где М(x₁,x₂,…x_n) – точка n-мерного пространства, при стремлении точки М к точке М₀(x₁⁰,x₂⁰,…x_n⁰) любым образом, если для всякого сколь угодно малого >0 существует такое число >0, что из условия < , где 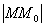- расстояние между точками М и М₀, следует < .

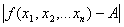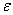Обозначается:

А .

Пусть z=f(x,y). Придадим x и y приращения 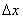и 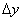. Получим приращение функции z=f(x,y). Если

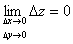, (1)

т.е. бесконечно малым аргументам соответствует бесконечно малое приращение функции, то говорят, что функция непрерывна.

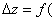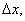Распишем x₀+ y+ 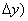-f(x₀,y₀) и положим x₀₊ x=x,y₀+ 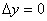,то выражение(1) можно записать в виде

f(x,y)=f(x ₀,y₀), (2)

т.е. непрерывность функции означает, что ее предел равен ее значению от пределов аргументов.

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области. Если в некоторой точке не выполняется условие (2), то эта точка называется точкой разрыва.