Метод интегрирования подстановкой

Интегрирование методом подстановки.

Суть метода заключается в том, что мы вводим новую переменную, выражаем подынтегральную функцию через эту переменную, в результате приходим к табличному (или более простому) виду интеграла.

Очень часто метод подстановки выручает при интегрировании тригонометрических функций и функций с радикалами.

Пример.

Найти неопределенный интеграл .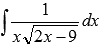

Решение.

Введем новую переменную 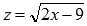. Выразим х через z:

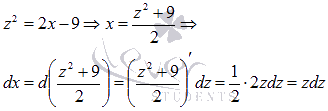
Выполняем подстановку полученных выражений в исходный интеграл:

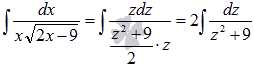
Из таблицы первообразных имеем .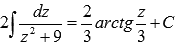

Осталось вернуться к исходной переменной х:

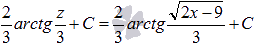
Ответ:

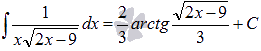
При интегрировании функций с иррациональностью вида 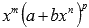, где m, n, p – рациональные числа, важно правильно выбрать выражение для введения новой переменной. Смотрите рекомендации в разделе интегрирование иррациональных функций.

Очень часто метод подстановки используется при интегрировании тригонометрических функций. К примеру, использование универсальной тригонометрической подстановки позволяет преобразовать подынтегральное выражение к дробно рациональному виду.

Метод подстановки позволяет объяснить правило интегрирования .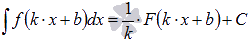

Вводим новую переменную 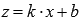, тогда

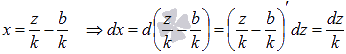
Подставляем полученные выражения в исходный интеграл:

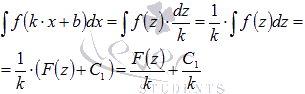
Если принять 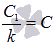и вернуться к исходной переменной х, то получим

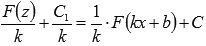
По частям

Интегрирование по частям.

Интегрирование по частям основано на представлении подынтегрального выражения в виде произведения 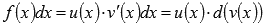и последующем применении формулы 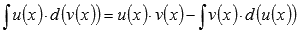. Этот метод является очень мощным инструментом интегрирования. В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата. Для примера найдем множество первообразных функции арктангенс.

Пример.

Вычислить неопределенный интеграл .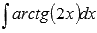

Решение.

Пусть 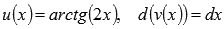, тогда

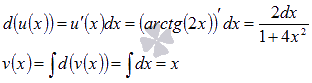
Следует отметить, что при нахождении функции v(x) не прибавляют произвольную постоянную С.

Теперь применяем формулу интегрирования по частям:

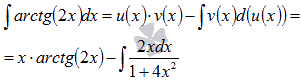
Последний интеграл вычислим по методу подведения под знак дифференциала.

Так как 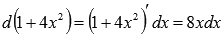, то 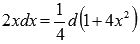. Поэтому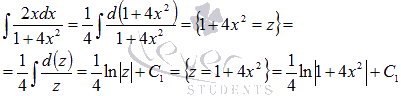

Следовательно,

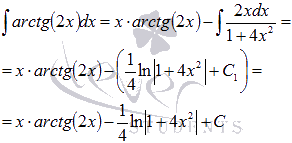
где .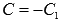

Ответ:

.

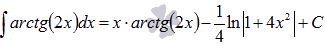Основные трудности при интегрировании по частям порождает выбор: какую часть подынтегрального выражения брать за функцию u(x), а какую за дифференциалd(v(x)).

5,6 интегрирование правильных и неправильных рац дробей

Для интегрирования рациональной функции P(x)Q(x), где P(x) и Q(x) − полиномы, используется следующая последовательность шагов:

Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;

Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;

Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;

Вычислить интегралы от простейших дробей.

Рассмотрим указанные шаги более подробно.

Шаг 1. Преобразование неправильной рациональной дроби

Если дробь неправильная (т.е. степень числителя P(x) больше степени знаменателя Q(x)), разделим многочлен P(x) на Q(x). Получим следующее выражение:

P(x)Q(x)=F(x)+R(x)Q(x),

где R(x)Q(x) − правильная рациональная дробь.