Макросостояние и фазовый ансамбль

Макросостояние системы имеет определенные значения термодинамических характеристик. Одному макросостоянию соответствует множество различных микросостояний.

Фазовый ансамбль есть множество микросостояний с одинаковыми значениями макрохарактеристик, т. е. относящихся к одному макросостоянию.

Функция распределения микросостоянийфазового ансамбля

Вероятность обнаружения микросостояния в единице объема фазового пространства около точки X называется плотностью вероятности

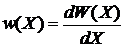. (2.3а)

Любое микросостояние занимает одинаковый фазовый объем. Тогда 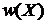равно числу микросостояний в единице объема фазового пространства, т. е. плотности микросостояний фазового ансамбля. Вероятность нахождения системы в объеме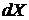

. (2.3)

Интегрируя

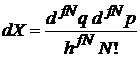, (2.2)

находим число микросостояний

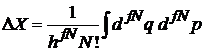. (2.3б)

Условие нормировки

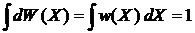. (2.4)

Теорема Лиувилля

Идеальный газ описывается гамильтонианом .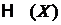

Фиксируем макросостояние, т. е. термодинамические параметры. Макросостояние реализуется ансамблем микросостояний. В фазовом пространстве они отображаются множеством точек, которые передвигаются с течением времени.

Теорема Лиувилля утверждает – движение точек фазового ансамбля подобно течению несжимаемой жидкости, сохраняющей свой объем и плотность. Плотность микросостояний зависит от гамильтониана и не изменяется с течением времени.

Теорему доказал Жозеф Лиувилль в 1838 г. Теорема используется для получения функции распределения состояний в фазовом пространстве.

Доказательство теоремы:

Рассмотрим бесконечно малый объем фазового пространства в форме цилиндра с осью вдоль 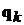. Основания 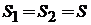перпендикулярны к оси, длина образующей .

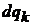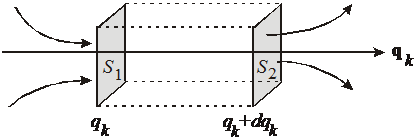
Микросостояния с плотностью 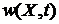входят в объем и выходят из него.

За 1с входит число состояний, заполняющих цилиндр сечением 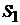и длиной образующей, равной скорости :

.

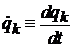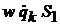От точки к точке меняется плотность и скорость, тогда число выходящих состояний

,

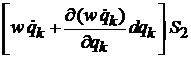где использовано

.

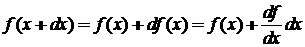Если с течением времени плотность w изменяется, тогда в объеме рождаются или исчезают состояния. За 1с в объеме 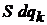появляется число состояний

.

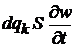Каждое состояние описывает реальную систему, поэтому число состояний сохраняется и выполняется баланс

«число появившихся» = «число вошедших» – «число вышедших»:

.

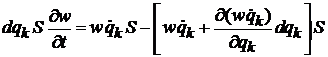Сокращаем подобные и получаем

.

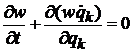Результат обобщаем на случай изменения 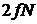координат

.

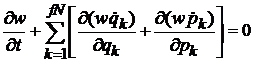Раскрываем круглые скобки

.

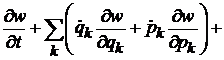
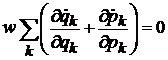Последняя скобка равна нулю согласно уравнениям Гамильтона (2.1)

, .

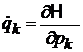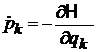Учитывая

,

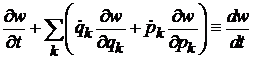получаем

.

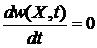Плотность микросостояний фазового ансамбля не изменяется при его движении.

Следствия теоремы

А. Согласно теореме число микросостояний ансамбля и плотность микросостояний сохраняются, тогда фазовый объем элемента ансамбля не изменяется с течением времени

,

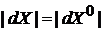изменяется лишь форма объема. Учитываем

,

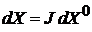где J – якобиан преобразования между начальными и текущими координатами. Тогда

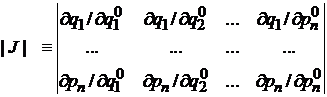= 1.

Модуль якобиана, связывающего начальные и текущие фазовые координаты, равен единице.

Б. Проекция фазового объема на любую координатную плоскость независима от других. Фазовый объем не изменяется, тогда площадь каждой проекции постоянна. Для одной частицы в проекции на плоскость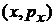

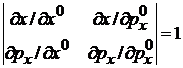. (2.5)

В. Для стационарной системы функция распределения не изменяется с течением времени и может зависеть только от интегралов движения. Если система как целое неподвижна и не вращается, то функция распределения зависит от полной энергии, т. е. от гамильтониана:

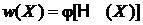. (2.6)

Г. Для равновесной консервативной системы

.

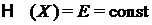Система с равной вероятностью обнаруживается в любом из доступных микросостояний.

Д. Теорема не выполняется для диссипативных систем, т. е. при наличии трения, неупругих соударений, когда уравнения Гамильтона (2.1) неприменимы.

ПРИМЕР

Одномерный гармонический осциллятор (двухатомная молекула с упругой связью, матический маятник, шарик на пружине, и т. д.) колеблется с частотой ω и имеет энергию E. Найти фазовую траекторию. Проверить выполнение теоремы Лиувилля.

1. Если энергия системы фиксирована, то микросостояния в фазовом пространстве движутся по гиперповерхности. Для одномерной системы из одной частицы координаты фазового пространства (x,p). Гамильтониан осциллятора приравниваем полной энергии

.

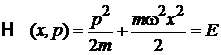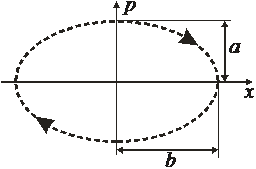
2. Получаем уравнение фазовой траектории, по которой двигаются микросостояния:

.

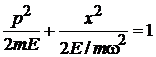Микросостояния отличаются начальной фазой. Сравниваем с уравнением эллипса на плоскости (y,z)

,

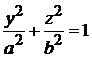находим полуоси вдоль p и x

, .

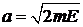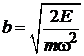3. Число микросостояний

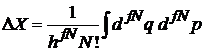. (2.3б)

При 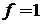, 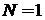интеграл равен площади эллипса

,

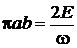тогда

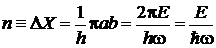, (П.2.4)

где 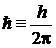. Следовательно, энергия осциллятора квантуется

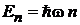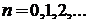, , (П.2.4а)

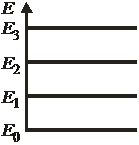
спектр эквидистантный. Горизонтальная линия на рис. соответствует состоянию с определенной энергией. 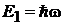– интервал эквидистантного спектра осциллятора.

4. Для получения якобиана

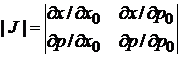
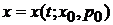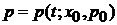необходимо найти и , где 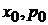– начальные координата и импульс, т. е. при .

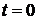Используем уравнения Гамильтона

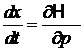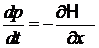, . (2.1)

Подставляем гамильтониан осциллятора

,

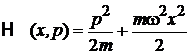получаем

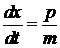– связь скорости с импульсом,

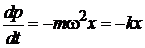– 2-й закон Ньютона ,

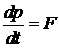где 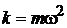– коэффициент жесткости упругой силы F;

.

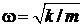Дифференцируем первое уравнение

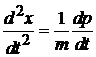
и подставляем второе

.

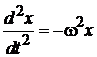Общее решение

,

.

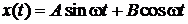Начальные значения

,

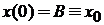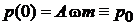
дают

, ,

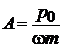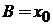тогда координаты микросостояния

,

.

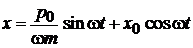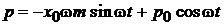С течением времени микросостояние движется по эллипсу по часовой стрелке.

5. Вычисляем якобиан

.

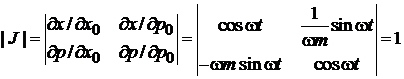Теорема Лиувилля выполняется.