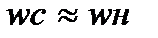Динамические свойства двухмассовой модели эп

С помощью передаточных функций двухмассойвой системы 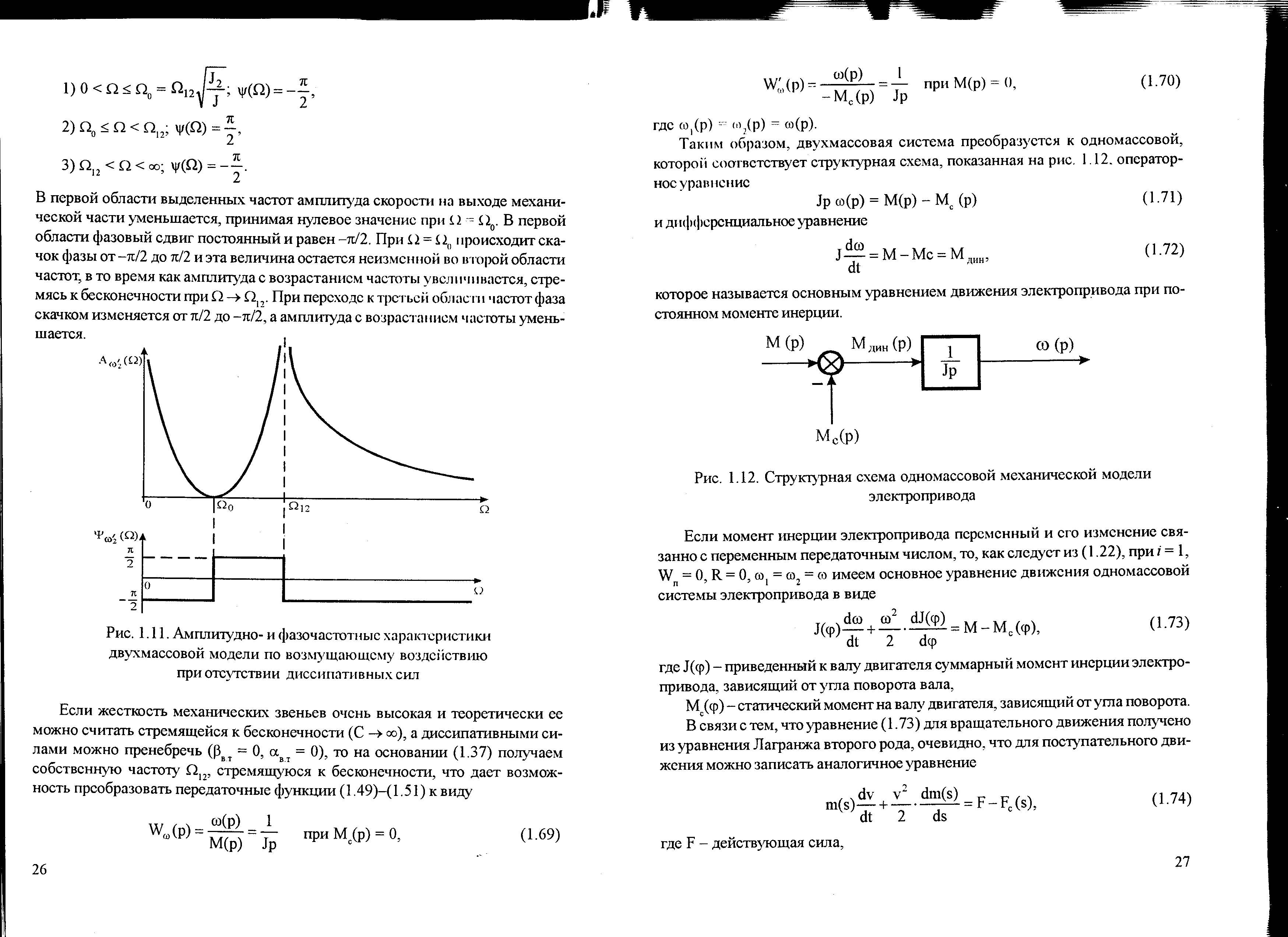можно исследовать динамические свойства механической части электропривода, применяя амплитудно-фазовые характеристики (АФХ). Переход от передаточных функций к АФХ осуществляется простой подстановкой р=jΩ,

где Ω – угловая частота входного воздействия.

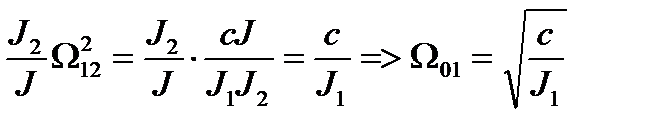Для примера рассмотрим динамические свойства двухмассовой системы без диссипативных сил. Полагая 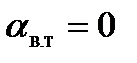найдем АФХ

-собственная частота колебаний первой массы при неподвижной второй массе.

Получим:

При анализе можно выделить три области частот (рис. 1.11):

1) 0 < Ω ≤ Ω₀₁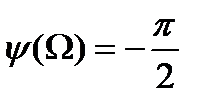

2) Ω₀₁ ≤ Ω <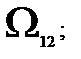

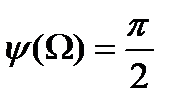
3) 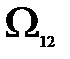< Ω < ∞;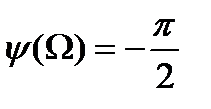

В первой области выделенных частот амплитуда скорости на выходе механической части уменьшается, принимая нулевое значение при Ω=Ω₀. В первой области фазовый сдвиг постоянный и равный –π/2. При Ω=Ω₀ происходит скачок фазы от –π/2 до π/2 и эта величина остается неизменной во второй области частот, в то время как амплитуда с возрастанием частоты увеличивается, стремясь к бесконечности при Ω→Ω₁₂. При переходе к третьей области частот фаза скачком изменяется от π/2 до -π/2, а амплитуда с возрастанием частоты уменьшается.

Если жесткость механических звеньев очень высокая и теоретически ее можно считать, стремящейся к бесконечности (с→∞), а диссипативными силами можно пренебречь ( 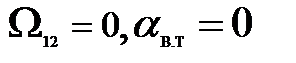), то получаем собственную частоту Ω₁₂, стремящуюся к бесконечности,

7.МОДЕЛЬ,структурная схема и уравннеие движения одномассовой системы эп

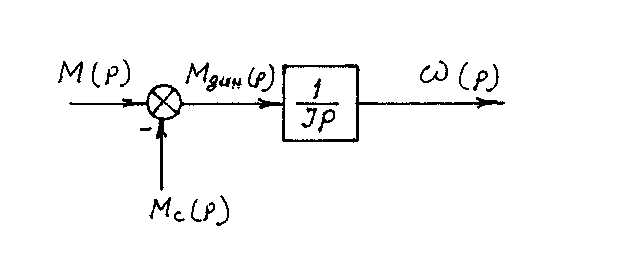
Таким образом, двухмассовая система преобразуется к одномассовой, которой соответствует структурная схема, показанная на рис. 1.12, операторное уравнение

Jp ω(p)=M(p)–Mc(p)

и дифференциальное уравнение

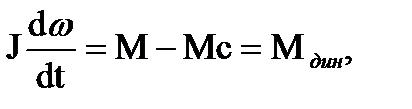(1.72)

которое называется основным уравнением электропривода при постоянном моменте инерции.

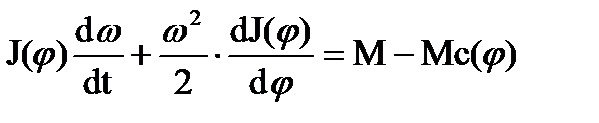- ур-ие движения при наличии нелин. механизмов (1.73)

где J(φ) – приведенный к валу двигателя суммарный момент инерции электропривода, зависящий от угла поворота вала,

Мс(φ) – статический момент на валу двигателя, зависящий от угла поворота.

Полностью очевидно, что при J=const (1.73) преобразуется к (1.72), где возможны частные случаи:

1) М_дин>0, тогда 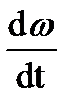>0 → разгон,

2) М_дин<0, тогда 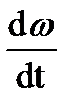<0 → торможение,

3) М_дин=0, тогда 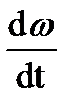=0, что соответствует установившемуся движению при ω_нач>0 и покою при ω_нач=0.

Заметим, что в установившемся движении М_дин=0 и М=М_с, т.е. электромагнитный момент равен статическому.

8.ДИНАМИЧЕСКИЕ СВОЙСТВА ОДНОМАССОВОЙ СИСТЕМЫ ЭП.Проанализируем динамические свойства одномассовой системы. АФХ будет иметь вид: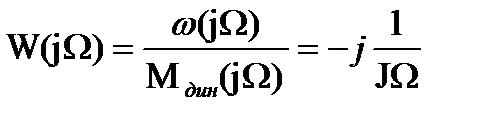

с амплитудно-частотной характеристикой

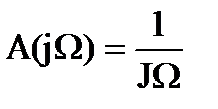
и фазо-частотной характеристикой (рис. 1.13)

.

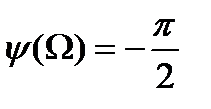Можно видеть, что одномассовая система электропривода является фильтром низких частот, т.е. она пропускает частоты порядка 5-10 Гц и демпфирует более высокие частоты. Это свойство механической части электропривода используется при применении широтно-импульсной модуляции (ШИМ) в современных электроприводах, где механическая часть реагирует в основном на низкочастотную составляющую входного воздействия.

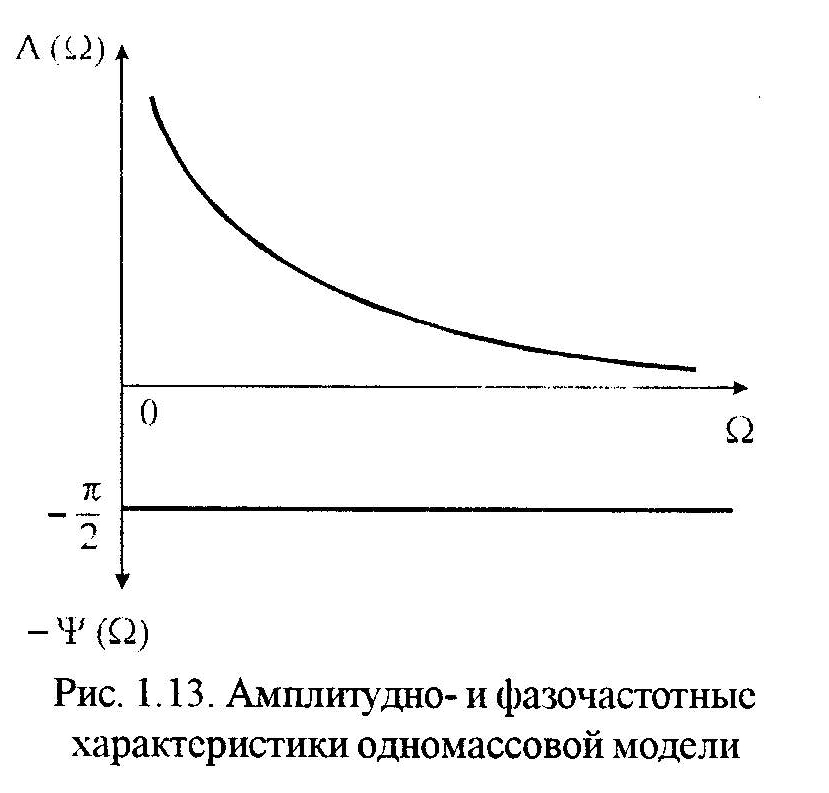Теперь сопоставим амплитудно- и фазо-частотные характеристики двух- и одномассовой систем (см. рис. 1.11 и 1.13). Можно видеть, что свойства двухмассовой системы в диапазоне частот 0<Ω<Ω₀ и Ω₁₂<Ω<∞ подобны свойствам одномассовой системы. В диапазоне частот W₀<W<W₁₂ динамические свойства двухмассовой системы существенно отличаются от динамических свойств одномассовой системы. Знание резонансных частот имеет существенное значение при частотном управлении электроприводом, когда эти резонансные частоты, если они входят в диапазон рабочих частот, необходимо обходить ступенчатым изменением плавного входного задания.

Если жесткость механических звеньев очень высокая и теоретически ее можно считать, стремящейся к бесконечности (с→∞), а диссипативными силами можно пренебречь ( )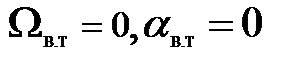

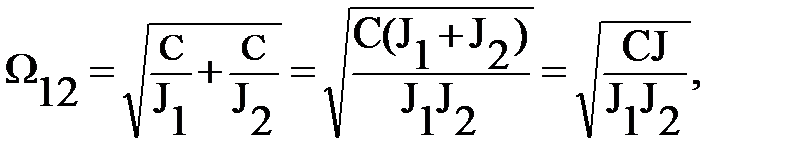(1.37)

получаем собственную частоту Ω₁₂, стремящуюся к бесконечности, что дает возможность преобразовать передаточные функции

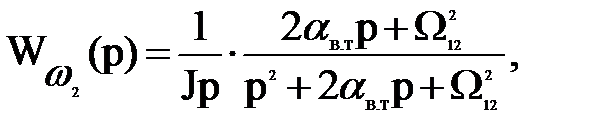
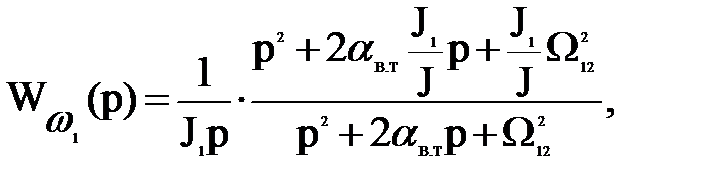
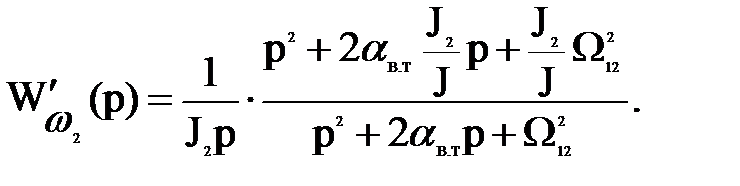к виду

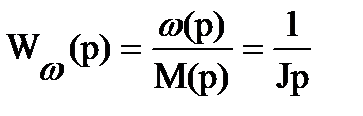при Мс(р)=0 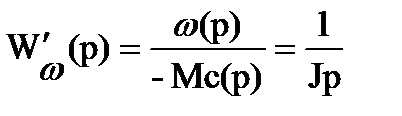при М(р)=0

где ω₁(р)= ω₂(р)= ω(р).

9.. ПРИВЕДЕНИЕ СИЛ, МОМЕНТОВ СОПРОТИВЛЕНИЯ, МОМЕНТОВ ИНЕРЦИИ И МАСС К ВАЛУ ЭД ДЛЯ ЛИНЕЙНЫХ ПМ

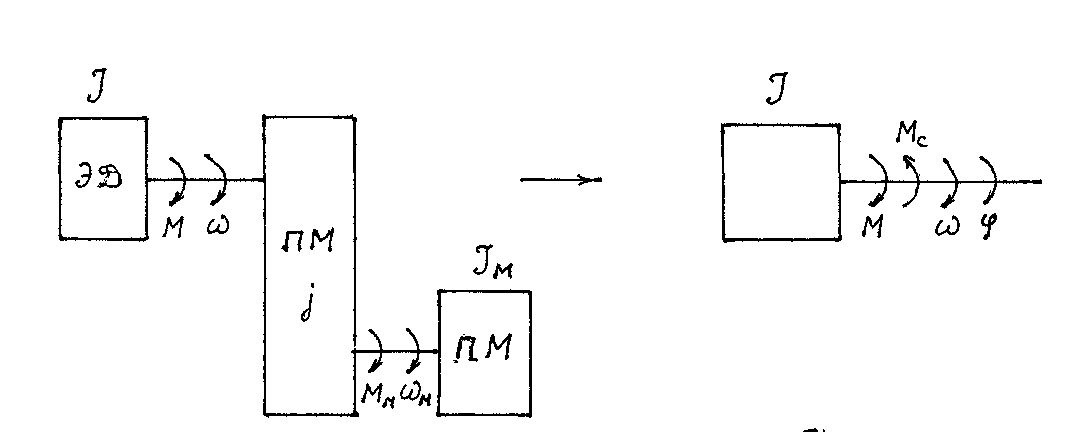
С целью упрощения реальную систему электропривода приводят к одной оси, чаще всего к валу электродвигателя со скоростью ω. При этом механические звенья электропривода принимаются абсолютно жесткими.

В результате приведения реальная многомассовая система (рис. 1.14 а) приводится к одномассовой системе (рис. 1.14 б), имеющей суммарный момент инерции J, статический момент Мс, угловую скорость ω и угол поворота вала φ.

При принятом допущении на основании закона сохранения энергии имеем равенство:

Мсω = М_Мω_Н,

из которого находим выражение для статического Мс (приведенного 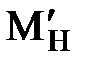) момента

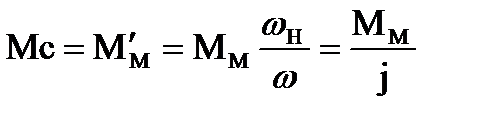(1.79)

Следовательно, статический момент на валу электродвигателя при отсутствии потерь в передаче численно равен моменту сопротивления М_М на валу исполнительного механизма ИМ, деленному на передаточное число j. В этом и состоит сущность приведения моментов сопротивления к валу электродвигателя.

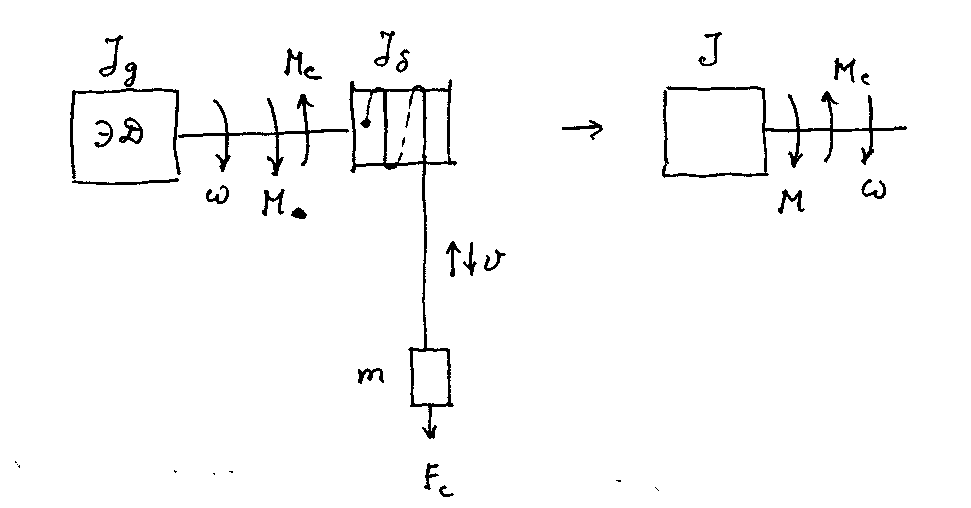При поступательном движении исполнительного механизма (рис. 1.15 а) и допущении об идеальности передачи с соблюдением закона сохранения энергии имеет равенство

Мсω = Fс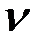

где 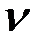– линейная скорость механизма,

Fc – сила сопротивления в установившемся движении,

Мс – эквивалентный статический момент на валу двигателя одномассовой системы (рис. 1.15 б).

,

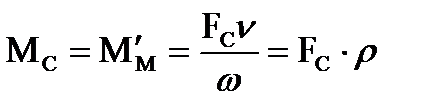где ρ – радиус приведения поступательного движения к вращательному.

Для линейных передаточных механизмов (j=const, ρ=const) рассмотрим приведения моментов инерции и масс к валу электродвигателя. При вращательном движении исполнительного механизма (см. рис. 1.14 а) и идеальном ПМ кинетическая энергия неприведенной системы должна равняться кинетической энергии приведенной системы (см. рис. 1.14 б), т.е.

,

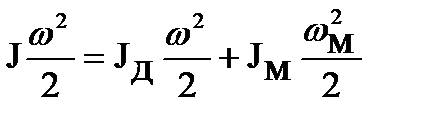откуда находим суммарный момент инерции приведенной системы:

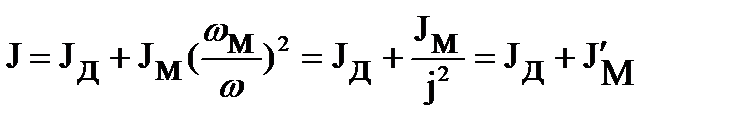
где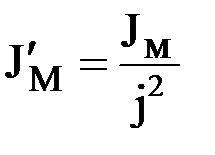

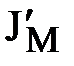– приведенный к валу электродвигателя момент инерции механизма.

Для поступательного движения исполнительного механизма (см. рис. 1.15а) записываем равенство кинетических энергий приведенной и неприведенной систем:

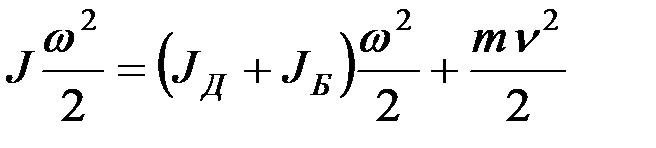
из которого получаем

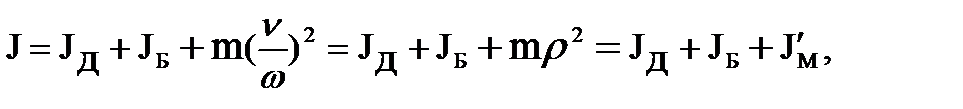
где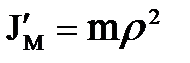

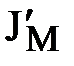– приведенный к валу электродвигателя момент инерции поступательно движущейся массы m,

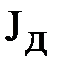– момент инерции ротора электродвигателя,

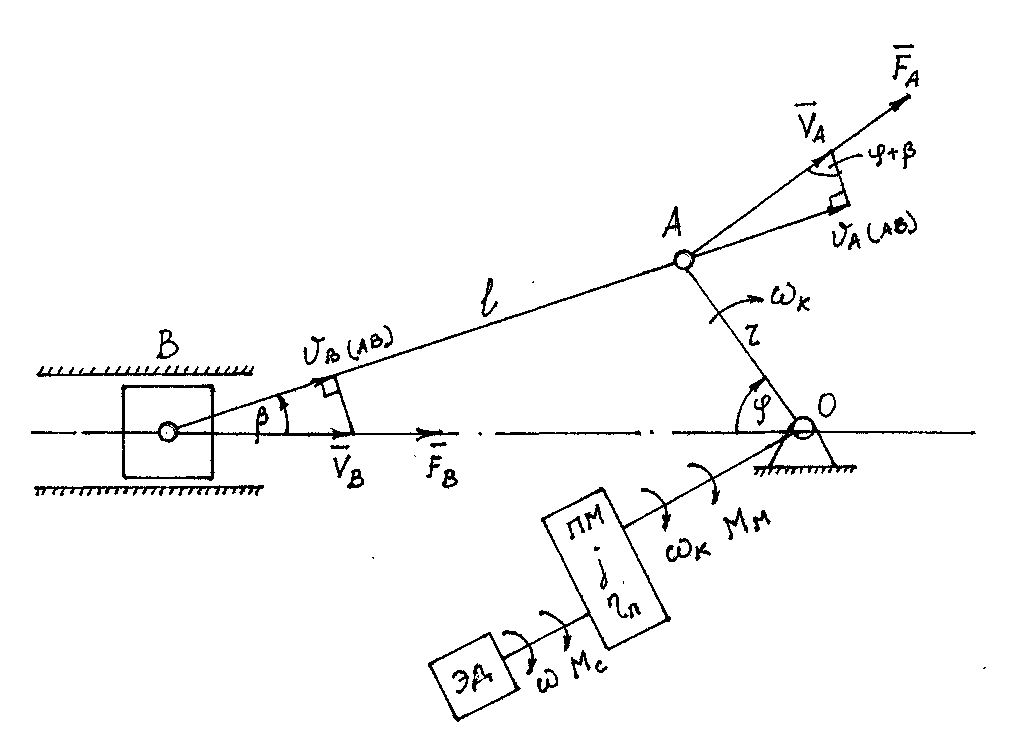
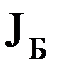– момент инерции барабана, соединенного с ротором ЭД.

Следовательно, приведенный к валу электродвигателя момент инерции поступательно движущейся массы равен произведению этой массы на квадрат радиуса инерции.

10.Приведение сил, моментов сопротивления, моментов инерции и масс к валу ЭД для нелинейных ПМ

на примере кривошипно-шатунного механизма (рис. 1.16). Пренебрегаем потерями в кривошипно-шатунном механизме и массой его элементов.

По закону сохранения энергии

F_В 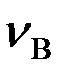= F_A ,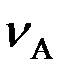

откуда

F_A= F_В ,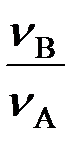

Где 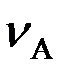=ω_К·r ,

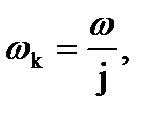
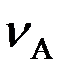– линейная скорость точки А,

ω_К – угловая скорость кривошипа АО,

r – радиус кривошипа,

ω – угловая скорость ротора электродвигателя,

j – передаточное число ПМ.

Поскольку при ω_К=const скорость ползуна В изменяется как по величине, так и по направлению при изменении угла поворота φ кривошипа ОА, то и сила в точке А будет функцией угла, т.е. F_A=F(φ).

Момент силы F_A относительно точки О

M_O(F_A)= F_A·r= F_В·r· 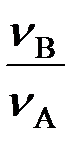=М_М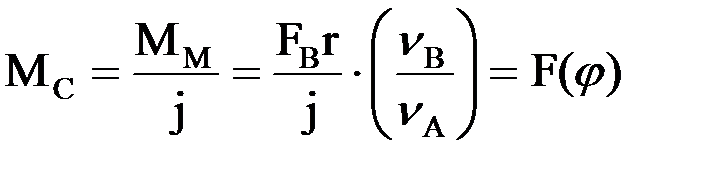

Обозначим m_B как массу ползуна и перемещаемого им изделия. Тогда кинетическая энергия движущейся массы m_B будет равна

W_B=m_B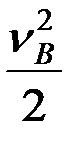

Приведем эту кинетическую энергию в точку А с фиктивной массой m_A, имеющей линейную скорость :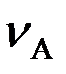

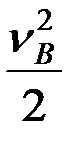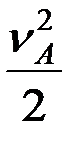m_B = m_A m_A=m_B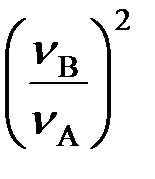

Момент инерции точечной массы m_A относительно оси О по определению равен

J₀(m_A)=J_M= m_Ar­­­²=m_Br­­­²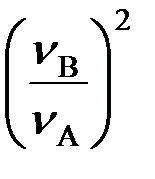

Приведение этого момента инерции к валу электродвигателя выполняется в соответствии с правилом (1.82):

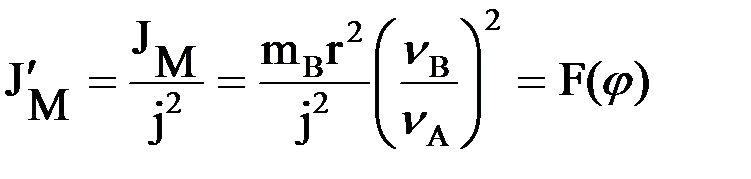
Для аналитического определения Мс и необходимо найти отношение 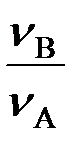. С этой целью воспользуемся следствием одной из теорем теоретической механики: при плоском движении проекции скоростей двух точек на прямую, проходящую через эти точки, равны, т.е.

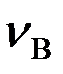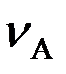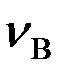_(АВ) = _(АВ) cosβ= 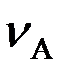sin(φ+β),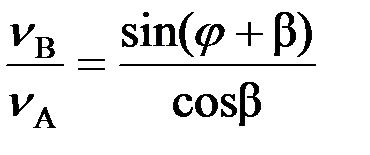

или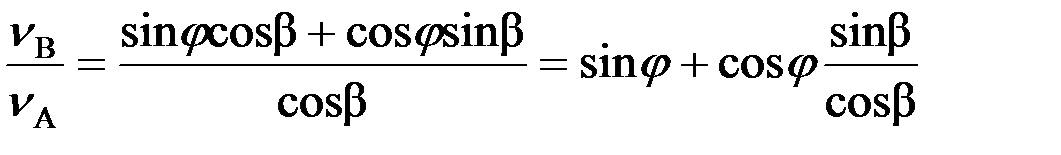

Для треугольника ОАВ (рис. 1.16) по теореме синусов имеем

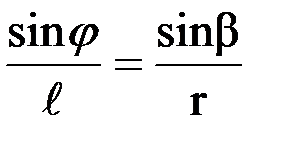
откуда

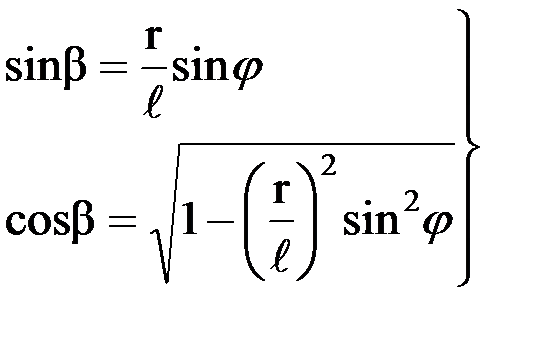
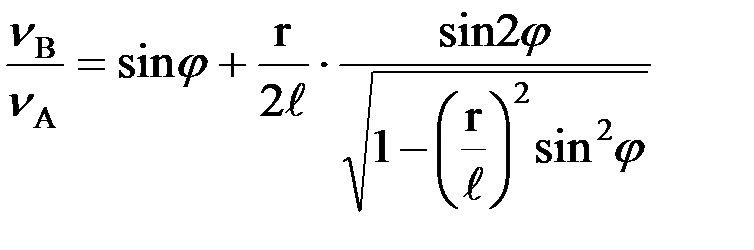
Теперь можно записать аналитическое выражение для приведенного к валу электродвигателя момента сопротивления

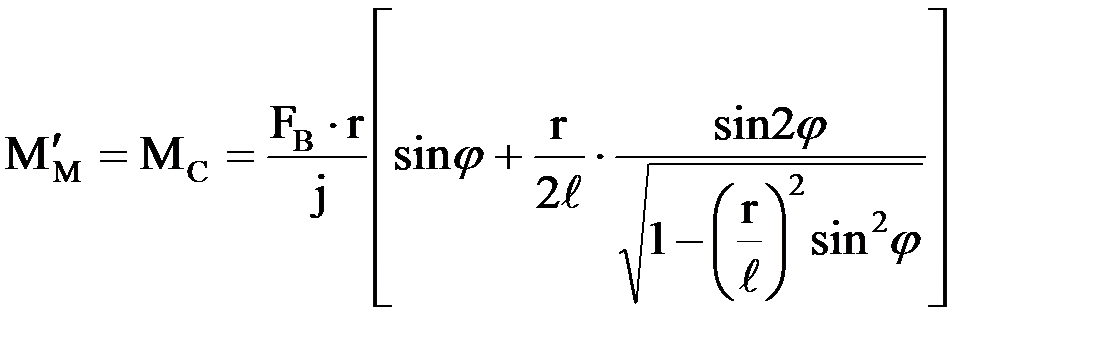
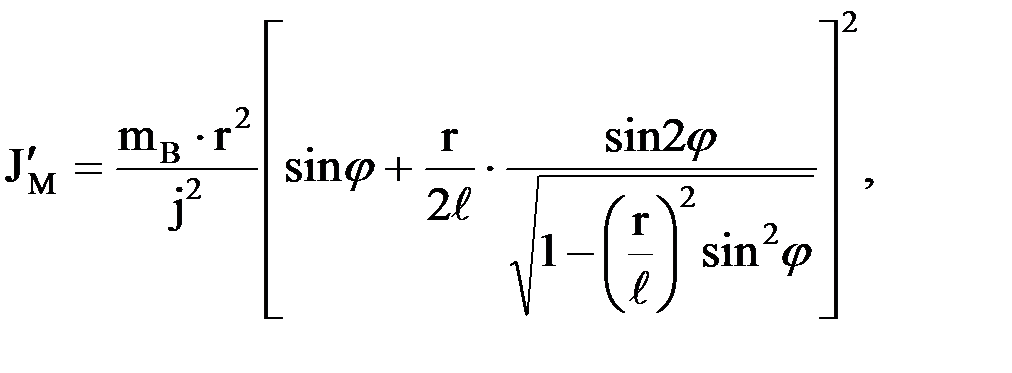
которые являются функцией угла поворота φ кривошипа ОА.

Расчеты динамики электропривода при переменном моменте инерции весьма сложные. Поэтому в расчетах обычно учитывают фактическую зависимость Мс=F(φ), а момент инерции принимают постоянным, равным среднему значению.

Момент инерции передаточного механизма в большинстве своем неизвестен, поэтому его принимают равным (10-30)% от момента инерции ротора электродвигателя, т.е.

J_ПМ=(0,1÷0,3)J_Д

В общем случае суммарный момент инерции электропривода, приведенный к валу электродвигателя, вычисляются по формуле:

J=(1,1÷1,3)J_Д+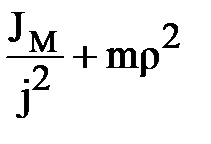

11ОПТИМАЛЬНОЕ ПЕРЕДАТОЧНОЕ ЧИСЛО РЕДУКТОРА

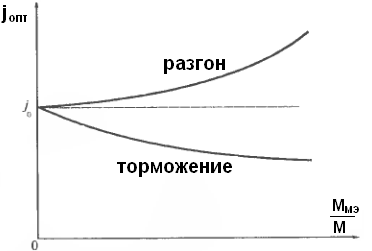
1) По минимуму времени переходного процесса:

a) первый способ: (ЭДМ=const, Jд=const) (Исполн-й мех-м Mн,wн,Jн)

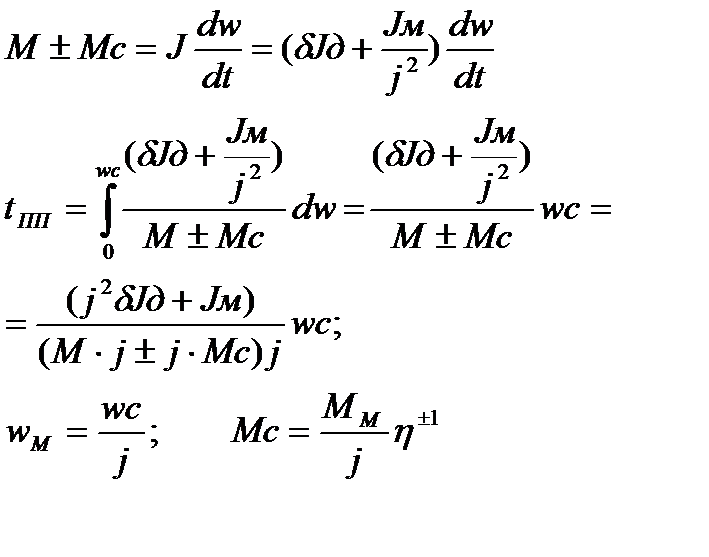
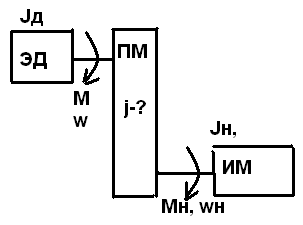
+ торможение , - разгон

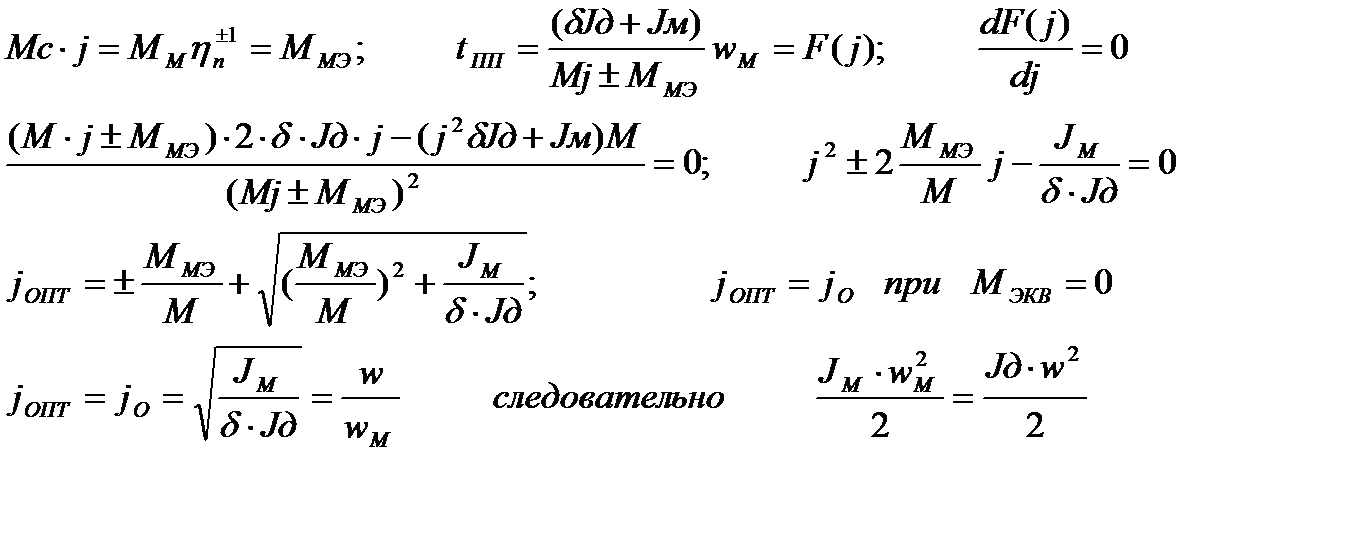
При оптимальном j и отсуствия момента нагрузки на валу, кинетическая энергия механизма = кинетической энергии ЭД вместе с редуктором

b) второй способ (ЭД P =const) (Исполн-й мех-м Mн,wн,Jн)

М=const; М=Мном 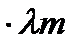;