Определение коэффициента поверхностного натяжения жидкости

Цель работы: ознакомится с различными экспериментальными методами определения коэффициента поверхностного натяжения жидкости.

Теоретическая часть

Поверхностное натяжение– это термодинамическая характеристика поверхности раздела двух фаз определяемая обратимой изотермической работой образования единицы площади этой поверхности:

. (1)

Величину 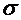называют также коэффициентом поверхностного натяжения, в СИ 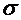измеряется в Дж/м².

Работа образования новой поверхности затрачивается на преодоление сил межмолекулярного взаимодействия при переходе молекул из объема тела в поверхностный слой. Рассмотрим переход молекулы из объема жидкости к ее свободной поверхности (рис.1).

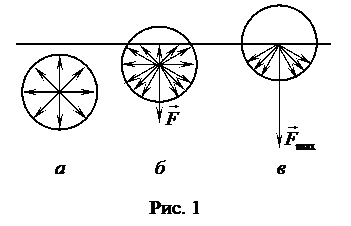Внутри жидкости (положение а) силы взаимодействия с окружающими молекулами уравновешены. При приближении к границе раздела с воздухом, в котором плотность вещества существенно ниже, чем в жидкости, воздействие на молекулу со стороны остальных молекул жидкости частично неуравновешенно (положение б). Появится результирующая сила ( ), направленная внутрь жидкости по нормали к границе раздела фаз. Максимальное значение эта сила будет иметь тогда, когда молекула достигнет поверхности жидкости (положение в). При движении молекулы к поверхности против указанной силы будет совершена работа:

, (2)

поэтому молекулы поверхностного слоя обладают некоторой добавочной потенциальной энергией.

Известно, что при переходе к равновесию всякая система стремится к минимуму своей потенциальной энергии. Благодаря поверхностному натяжению при отсутствии внешних воздействий жидкость принимает форму шара, так как при заданном объеме шар имеет наименьшую поверхность. Поэтому поверхностное натяжение можно рассматривать как силу, действующую на единицу длины контура на поверхности и стремящуюся сократить поверхность до минимума:

. (3)

Из (3) видно, что коэффициент поверхностного натяжения может также измеряться в Н/м. Сила поверхностного натяжения направлена по касательной к поверхности.

При повышении температуры поверхностное натяжение уменьшается и обращается в нуль при достижении критической точки. Поверхностное натяжение уменьшается также под воздействием поверхностно-активных веществ.

Существуют различные способы определения коэффициента поверхностного натяжения жидкостей.

Метод отрыва кольца

Рассмотрим металлическое кольцо диаметром D и толщиной d, касающееся поверхности жидкости. При поднятии кольца над поверхностью жидкости между кольцом и поверхностью жидкости образуется пленка. На рис.2 эта картина показана в разрезе.

Пленка тянет кольцо вниз. В момент отрыва кольца сила, действующая со стороны пленки на кольцо, равна силе поверхностного натяжения. При этом внешняя поверхность пленки тянет кольцо вниз с силой, равной на основании формулы (3):

, (4)

где 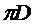- длина контура, на который действует сила 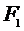, внутренняя поверхность пленки тянет кольцо вниз с силой:

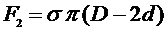. (5)

Кроме того, на кольцо действуют также сила тяжести ( ), направленная вниз, и сила, действующая со стороны пружины ( ), направленная вверх, которая по модулю на основании третьего закона Ньютона равна силе упругости пружины. В момент перед отрывом кольца система находится в равновесии. Тогда, применяя второй закон Ньютона, получаем выражение для модуля сил:

. (6)

Обозначим:

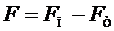, (7)

тогда выражение (6) с учетом (4), (5) и (7) запишется в виде:

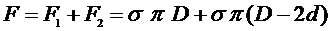. (8)

Из (8) получаем расчетную формулу:

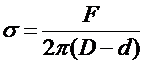. (9)

Следовательно, для определения 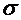нужно измерить силу, которую необходимо приложить к кольцу для ее отрыва от поверхности жидкости, и размеры кольца.

Экспериментальная часть

Описание установки и метод измерения

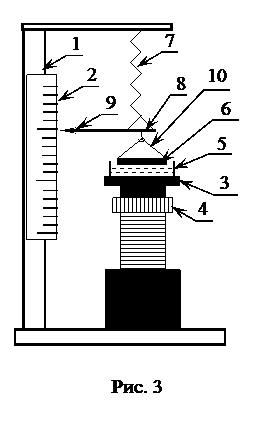
Прибор для определения коэффициента поверхностного натяжения состоит из специальной стойки (1), к которой прикреплена вертикальная миллиметровая шкала (2). Перед шкалой установлен столик (3), который может перемещаться вверх и вниз с помощью винтового механизма (4). На столике помещается низкий сосуд (кристаллизатор) (5) с испытуемой жидкостью. Кольцо (6) с помощью проволочной петли (10) подвешивается к пружине (7), которая служит для измерения силы поверхностного натяжения F. Между кольцом и пружиной находится полка (8), на которую кладут разновесы для градирования пружины. Растяжение пружины определяют по шкале (2) с помощью указателя (9). Для определения размеров кольца используется штангенциркуль.

Выполнение работы

1. Измерить размеры кольца штангенциркулем: внешний диаметр D и толщину кольца d не менее 5 раз в различных местах, результаты измерений занести в таблицу. Вычислить средние значения 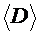и .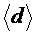

№	D, мм	d, мм
1.
2.
3.
4.
5.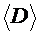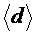
, м	, м

2. Тщательно протереть кольцо чистой тряпочкой. Подвесить кольцо к пружине, держа его за проволочную петлю (10), кольцо руками не трогать.

3. Опустить столик (3) винтовым механизмом (4) в нижнее положение.

4. Проградуировать пружину. Градуировка пружины заключается в нахождении зависимости ее удлинения от приложенной силы, которой является сила тяжести, действующая на разновесы, находящиеся на полке (8). (Так как к пружине подвешено кольцо, то сила тяжести, действующая на кольцо, и сила тяжести, действующая на разновес, который мы кладем на полку (8), будут уравновешиваться силой, действующей со стороны пружины 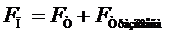, но, вспоминая выражение (7): 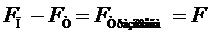, кроме того F входит в расчетную формулу (9) для коэффициента поверхностного натяжения, таким образом при измерениях нет необходимости находить силу тяжести, действующую на кольцо.) Для этого необходимо определить положение указателя (9) по миллиметровой шкале (2), когда на полке (8) нет разновесов. Результат измерения занести в таблицу. Затем необходимо положить в центр полки (8) разновес 500 мг и определить положение указателя по шкале. Добавляя разновесы по 500 мг, каждый раз необходимо определять положение указателя по шкале (n) и рассчитывать силу F ( , где m- суммарная масса разновесов на полке (8), g- ускорение сводного падения 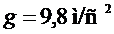). Данные заносятся в таблицу.

F, H
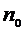n, мм
, мм

5. По данным таблицы построить градировочный график. Предполагаемый вид графика показан на рис.4.

6. Определить силу поверхностного натяжения. Для этого все разновесы снять с полки (8) (рис. 3), чистый кристаллизатор (5) поставить на столик (3) и налить в него дистиллированную воду, поднимая столик с помощью подъемного механизма (4), привести нижний край кольца в соприкосновение с жидкостью. Проследить, чтобы нижний край кольца равномерно касался поверхности жидкости, то есть был горизонтальным. При необходимости отрегулировать положение кольца. Затем, медленно и равномерно опуская столик, «уловить» равновесие перед отрывом кольца и заметить по шкале положение указателя 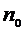. Опыт по отрыву кольца повторить не менее 5 раз, определяя положение указателя в момент отрыва. Результаты занести в таблицу. Найти среднее положение указателя при отрыве .

7. Отложив значение на ранее построенном градировочном графике (пример графика рис. 4), определить силу (F) поверхностного натяжения.

8. Вычислить по формуле (9) 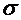. Вычислить абсолютную погрешность 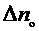и по графику определить величину .

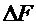9. Рассчитать абсолютную 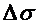и относительную 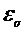погрешности. Записать окончательный результат и сравнить его с табличным с учетом погрешности

Метод отрыва капель

Поверхностное натяжение ( 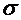) можно измерить по массе капли, оторвавшейся от вертикальной трубки (сталагмометра).

Капля жидкости на конце узкой трубки удерживается силами поверхностного натяжения. Если капля очень медленно увеличивает свой объем, то через некоторое время она оторвется. Это произойдет тогда, когда сила тяжести, действующая на каплю, станет равна силе поверхностного натяжения:

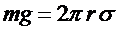, (10)

где m- масса капли, g- ускорение свободного падения, r- радиус шейки капли непосредственно перед отрывом, 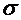- коэффициент поверхностного натяжения. Наибольшие трудности представляет измерение радиуса шейки капли (r), поэтому часто пользуются относительным методом.

Если кроме испытуемой жидкости взять эталонную жидкость, коэффициент поверхностного натяжения которой известен ( ), то из соотношений (10), записанных для испытуемой и эталонной жидкостей, предполагая, что радиус шейки капель испытуемой и эталонной жидкостей одинаковы, получим:

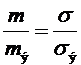. (11)

Массу отдельной капли исследуемой жидкости можно найти по формуле:

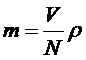, (12)

где V- объем некоторого числа N капель жидкости, оторвавшихся от конца трубки, р - плотность жидкости. Если через трубку пропустить точно такой же объем V эталонной жидкости, то:

. (13)

Подставив (12) и (13) в (11), получим расчетную формулу:

. (14)