Главные значения несобственных интегралов

Вернемся к интегралу 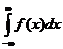. Его определение было следующим:

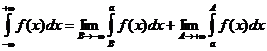(а - любое).

Обратите внимание на одну деталь: в этом определении два предела и величины А и В совершенно не связаныдруг с другом, они живут «каждый сам по себе».

Так вот, главным значением этого интеграла называется величина

.

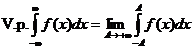(V.p. - первые буквы слов «valeur principale», что , в переводе с французского, и означает «главное значение»). Обратите внимание на то, что здесь только одинпредел. Это выражение получается из предыдущего, если завязать величины А и В соотношением .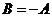

Если 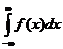не существует, но существует 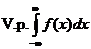, то говорят, что интеграл 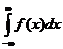существует в смысле главного значения.

Рассмотрим вычисление главного значения .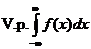

Пусть 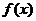- нечетная функция, то есть 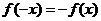. Тогда очевидно, что 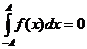и поэтому в данной ситуации .

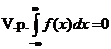Пусть теперь 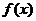- четная функция, то есть 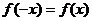. Тогда очевидно, что 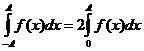и поэтому в данной ситуации .

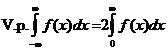В общем случае 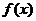можно представить в виде 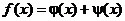, где

, .

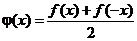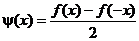Очевидно, что 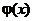есть четная функция, а 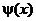- нечетная. Поэтому

,

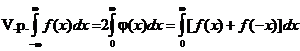что и является рабочей формулой для вычисления .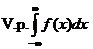

Рассмотрим теперь несобственные интегралы второго рода. Пусть с есть особая точка функци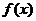и и 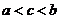. Тогда, как уже говорилось выше,

.

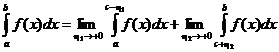Снова обратите внимание на то, что в этом определении двапредела и величины h₁ и h₂ никак друг с другом не связаны. Главное значение этого интеграла определяется так

,

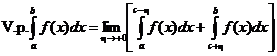то есть величины h₁ и h₂ стали одинаковыми и предел один.

Рассмотрим пример на вычисление главного значения. Пусть мы имеем интеграл 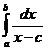и 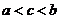. Тогда имеем

.

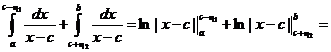
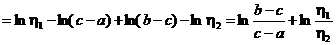Но если h₁ и h₂ никак друг с другом не связаны, то отношение 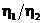может быть любым, и при 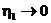, 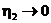предел не существует. Но если считать, что h₁ = h₂, то 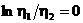и поэтому

,

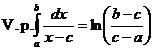и интеграл 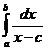существует в смысле главного значения.

8.8 Преобразование несобственных интегралов

Интегрирование по частям

Пусть функци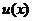и и 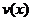непрерывны на промежутке 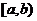и точка b является особой точкой по крайней мере для одной из них. Тогда, вспоминая формулу интегрирования определенных интегралов по частям, получим

.

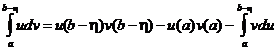Сделаем предельный переход 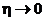. Переменная h есть в трех слагаемых. Если существуют два предела, то существует и третий, и мы получим

,

что является формулой интегрирования по частям в несобственных интегралах.

Для несобственных интегралов первого рода она принимает вид

.

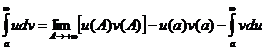Вывод аналогичен.

Замена переменных

Теорема. Пусть

1. 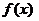определена на 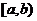(b - особая точка);

2. 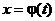, где на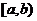 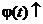и существует непрерывная ;

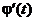3. 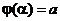и .

Тогда имеет место формула

.

Доказательство.

Пусть 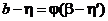. В силу непрерывност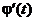и при 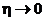также и 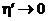. Вспоминая замену переменных в определенных интегралах, имеем:

.

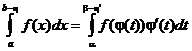После предельного перехода 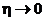, получаем

. <

Пример.

Рассмотрим интеграл 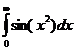, который называется интегралом Френеля. Вопрос о его сходимости не может быть решен на основании изученных нами признаков.

Сделаем замену переменных . Тогда 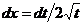и мы имеем:

.

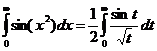Получившийся интеграл сходится по признаку Дирихле.

Интегралы Фруллани

Пусть

1. функция 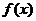определена и непрерывна при ;

2. существует конечный ;

3. .

Рассмотрим следующий интеграл:

.

Имеем

В первом интеграле сделаем замену переменных , во втором - : получаем

И теперь - самое интересное. Посмотрите на области интегрирования первого и второго интегралов:

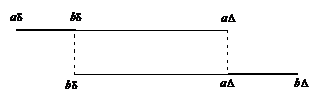
У них есть общая часть - отрезок 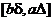. Подынтегральные функции одинаковы, интегралы вычитаются - следовательно, интегралы по этой области сокращаются. Остается

А теперь срабатывает первая теорема о среднем

,

где , .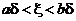

А теперь сделаем предельный переход при 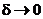, 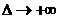. Тогда , и мы получаем

.

Интеграл 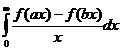называется интегралом Фруллани. Полученная формула позволяет легко вычислять их.

Интегральные неравенства

Неравенство Гёльдера.

Выведем одно из важнейших неравенств математического анализа - неравенство Гёльдера.

Пусть p и q - вещественные числа, такие, что

1. , :

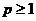2. (самое главное) .

Прежде, чем выводить само неравенство, выведем некоторые промежуточные формулы, чтобы потом не отвлекаться. Имеем

; ; ; .

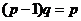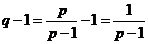А теперь - вперед!