Задач по курсу физики (часть 3)

Орёл, 2011 г.

Методические указания предназначены для студентов очной и заочной форм обучения Орловского государственного аграрного университета, изучающих курс физики по программе инженерных дисциплин для бакалавров.

Указания составлены в соответствии с ГОСТ и рабочими программами по физике специальностей 110301, 110302, 110303, 28102, 270102, 270115, 250203.

Рецензенты:

д.т.н., зав. кафедрой «Математика» Орел ГАУ Моисеенко А.М.

к.т.н., зав. кафедрой «Электроснабжение» Орел ГАУ Виноградов А.В.

В подготовке методических указаний принимали участие Иващук О.А., Гладких Ю.В., Васильева В.В., Гришина С.Ю., Зубова И.И., Ставчикова Л.Ф., Тверская Н.В., Гольцова Л.И.

Ответственный за выпуск Гладких Ю.В.

Обсуждено на заседании кафедры физики, протокол №__от «__»______2011г.

Методические указания одобрены методической комиссией факультета гуманитарных и естественнонаучных дисциплин, протокол №__от «__»____2011г. и методическим советом Орел ГАУ, протокол №__ от _______2011г.

©Гладких Ю.В., Иващук О.А.,

Гришина С.Ю., Зубова И.И.,

Васильева В.В., Ставчикова Л.Ф.,

Тверская Н.В., Гольцова Л.И.

Методические указания к решению задач

Решение физических задач следует проводить в определённой после-довательности и соблюдая ряд указанных ниже требований.

Выписать данные задачи в колонку в принятом стандартом

буквенном обозначении. Если необходимо обозначить несколько сходных величин, можно ввести большие и малые буквы или индексы (например, различные сопротивления в электрической цепи можно обозначить R₁, R₂,R₃,r и т.д.)

Величины, приведенные в условиях задачи, выразить в одной системе единиц, наиболее подхдящий для задачи(предпочтительно в СИ).

Вспонить физические законы, на основании которых следует производить решение задачи. Дать формулировку этих законов. Написать соответствующие им формулы.

4.Если это необходимо, сделать схематический чертёж (рисунок, график, схему), поясняющий содержание задачи. Например, озобразить тело с приложенными к нему силами, график изменения объема газа при нагревании, схему электрической цепи, ход лучей в оптических системах и т.д.

Решение задачи сопровождать краткими пояснениями.

Решение большинства задач сводится к составлению алгебраических уравнений, отражающих заданный физический процесс. Поэтому задачи необходимо доводить до конца не в числовом, а в буквенном виде. При таком способе ответ получается в виде формулы, которая позволяет проверить полученный результат, а промежуточные выкладки дают возможность проверить любую часть решения и исключить ошибки. Ответ, полученный в общем виде, позволяет сделать анализ решения, тогда как числовой ответ сделать это не даёт возможности.

Получив ответ в виде алгебраической формулы, следует проверить его на основании правил размерностей, то есть убедиться, что размерности правой и левой частей равенства совпадают.

Проверив совпадение размерностей, следует произвести анализ полученного ответа и выяснить, удовлетворяет ли он условиям задачи. Так, при решении квадратного уравнения получаются два ответе, один из которых может не удовлетворять данным задачи и его следует отбросить.

Произведя проверку, можно подставить в полученную формулу числовое значение величин, приведённых в условиях задачи. При арифмети-ческих подсчётах следует использовать правила приближенных вычислений и производить расчёты лишь с тем количеством значащих цифр, которое определяется условиями задачи. Если правило размерностей было проверено, то подставлять наименования в расчётную формулу не следует, так как это лишь загромождает расчёты. В окончательном результате наименование полученной величины записывается в СИ.

Записать ответ.

Пример решения задачи.

На дифракционную решетку нормально к ее поверхности падает парал-лельный пучок света с длиной волны λ = 0,5 мкм. Помещенная вблизи решетки линза проецирует дифракционную картину на плоский экран, удаленный от линзы на L = 1 м. Расстояние l между двумя максимумами интенсивности первого порядка, наблюдаемыми на экране, равно 20,2 см. Определить : 1) почтоянную d дифракционной решетки; 2) число n штрихов на 1 см. 3) число максимумов, которое при этом дает дифракционная решет-ка; 4) максимальный угол φ_max отклонений лучей, соответствующих последнему дифракционному максимуму.

Дано: λ = 0,5 мкм L = 1 м l = 20,2 см	Си: 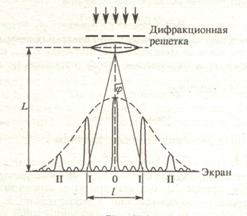0,5 ∙ 10-6 м 20,2 ∙ 10-2 м	Решение:
Найти: 1) d - ? 2) n - ? 3) kmax - ? 4) φmax - ?

1. Постоянная d дифракционной решетки, длина волны λ и угол φ отклонения лучей , соответствующий k – му дифракционному максимуму, связаны соот-ношением

, (4)

где k – порядок спектра, или в случае монохроматического света порядок максимума.

В данном случае k = 1, sinφ = tgφ (ввиду того, что l/2<< L), tgφ = (l/2)L (сле-дует из р. 1). С учетом последних трех равенств соотношение (4) примет вид

,

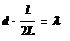
откуда постоянная решетки

.

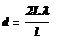
Подставляя данные, получим

d = 4,95 мкм.

2.Число штрихов на 1 см найдем из формулы

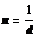
После подстановки числовых значений получим

n = 2,02 ∙ 10³ см^-1.

Для определения числа максимумов, даваемых дифракционной решеткой, вычислим сначала максимальное значение k_max , исходя из того, что макси-мальный угол отклонения лучей решеткой не может превышать 90⁰.

Из формулы (4) запишем

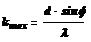
(5)

Подставляя сюда значения величин, получим

k_max= 9,9.

Число k обязательно должно быть целым. В то же время оно не может принять значение, равное 10, так как при этом значение sinφ должен быть больше единицы, что невозможно. Следовательно, k_max = 9.

Определим общее число максимумов дифракционной картины, полученной посредством дифракционной решетки. Влево и вправо от центрального максимума будет наблюдаться по одинаковому числу максимумов, равному k_max, т.е. всего 2k_max. Если учесть также центральный нулевой максимум, получим общее число максимумов

N = 2 ∙ 9 + 1 = 19.

4. Для определения максимального угла отклонения лучей, соответствующего последнему дифракционному максимуму, выразим из соотношения (5) синус этого угла:

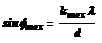
Отсюда

.

Подставив сюда значения k_max ,d, λ и произведя вычисления, получим

φ_max = 65,4⁰.

Геометрическая оптика.

· Фокусное расстояние сферического зеркала

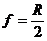, где R – радиус кривизны зеркала.

· Оптическая сила сферического зеркала

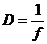
· Формула сферического зеркала

где а и Ь -— расстояния от полюса зеркала соответственно до предмета и изображения.

Если изображение предмета мнимое, то величина b берется со знаком минус.

Если фокус сферического зеркала мнимый (зеркало выпуклое), то величина f берется со знаком минус.

· Закон преломления света

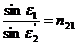
где 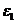— угол падения; — угол преломления; n21 = n2/n1 — отно­сительный показатель преломления второй среды относительно первой; n1 и n2 — абсолютные показатели преломления соответственно первой и второй сред.

· Предельный угол полного отражения при переходе света из среды более оптически плотной в среду менее оптически плотную

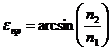(n₂<n₁)

· Оптическая сила тонкой линзы

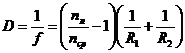
Где n_л – абсолютный показатель преломления линзы; n_cp – абсолютный показатель преломления окружающей среды (одинаковой с обеих сторон)

· Оптическая сила двух тонких сложенных вплотную линз

D=D₁+D₂

· Формула тонкой линзы

Где а – расстояние от оптического центра линзы до предмета; b – расстояние от оптического центра линзы до изображения.

Если фокус мнимый (линза рассеивающая), то величина f отрицательна.

Если изображение мнимое, то величина b отрицательна.

· Угловое увеличение лупы

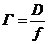
Где D – расстояние наилучшего зрения (D = 25 см)

Пример решения задачи.

На стеклянную призму с преломляющим углом θ =50° падает под углом ε₁= 30° луч света. Определить угол отклонения а луча призмой, если показатель преломления n cтекла равен 1,56.

Решение. Данную задачу целесообразно решать не в общем виде, как принято, а пооперационно, производя все промежуточные вычисле­ния. В этом случае мы несколько проигрываем в точности расчетов,

но выигрываем в наглядности и простоте вычислений. Из рисунка видно, что угол отклонения

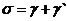(1)

а углы γ и γ' просто выражаются через углы 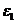, , 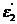, , 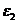которые последовательно и бу­дем вычислять:

1) из закона преломления sinε₁/sinε₂ имеем

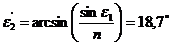
2) из рисунка, следует, что угол падения ε₂ на вторую грань призмы равен

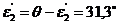
Угол ε₂ меньше предельного, поэтому на второй грани луч преломится и выйдет из призмы;

3) так как 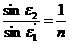, то . Те­перь найдем углы γ и γ':

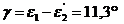
По формуле (1) находим

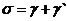=34,1°.

Задачи

1. вычислить увеличение лупы с фокусным расстоянием f = 3 см.

2. Полученное с помощью линзы изображение предмета на экра­не в пять раз больше предмета. Расстояние между предметом и эк­раном l = 150 см. Определить оптическую силу линзы и ее фокусное расстояние.

3. Какое увеличение β дает линза с оптической силой D = 5 дптр, если она находится на расстоянии а=25 см .от предмета?

4. Увеличение микроскопа β = 600. Определить оптическую силу D₁ объектива, если фокусное расстояние окуляра f₂ = 4 см, а длина тубуса L = 24 см.

5. Фокусные расстояния объектива и окуляра соответственно равны f₁=3 мм, f₂ = 3 см. Предмет находится на расстоянии s=3,l мм от объектива. Вычислить увеличение объектива и окуляра микроско­па.

6. Человек с нормальным зрением пользуется линзой с оптиче­ской силой D=16 дптр как лупой. Какое увеличение дает такая лупа?

7. Фокусное расстояние объектива микроскопа f₁=4 мм, окуляра f₂=5 см. Найти увеличение β этого микроскопа, если предмет поме­щен на расстоянии s = 4,2 мм от объектива микроскопа.

8. Оптическая сила объектива D=2,1 дптр. Расстояние от объ­ектива до экрана s'=10 м. Каково увеличение объектива?

9. Определить диаметр изображения среза мышечного волокна диаметром 9 • 10^{-4 см, рассматриваемого под микроскопом с фокус­ным расстоянием окуляра} f₁ = 14 см и объектива f₂=0,2 см. Расстоя­ние между фокусами объектива и окуляра 20 см.

10. Определить оптическую силу объектива, дающего десятикрат­ное увеличение. Расстояние от объектива до экрана s'=3,7 м.

11. Вогнутое сферическое зеркало дает на экране изображение предмета, увеличенное в Г = 4 раза. Расстояние а от предмета до зеркала равно 25 см. Определить радиус R кривизны зеркала.