Взаимодействие растворяемого вещества с растворителем
Существуют два основных механизма образования растворов электролитов.
По одному из них ионы, составляющие кристаллическую решетку растворяемого вещества, просто переходят в раствор. Этот механизм, называемый ионофорным, присущ солям.
По другому механизму, называемому ионогенным, нейтральные молекулы, исходно не содержащие ионов, при растворении в воде распадаются на ионы. Классическим примером такого механизма образования раствора электролита является растворение в воде хлороводорода.
В первом случае образование раствора сопровождается разрушением кристаллической решетки, а во втором - разрывом связи в молекуле. Для обоих процессов требуются значительные затраты энергии.
Существуют методы расчета энергии разрушения кристаллической решетки с образованием отдельных ионов. В частности, для галогенидов металлов приближенные расчеты можно проводить, используя данные по энтальпии прямой реакции между галогеном и металлом, потенциалу ионизации металла, сродству электрона и энтальпии испарения соли и теплоемкостям. Расчеты показывают, что изменение энергии Гиббса при переходе из кристалла NaCl к отдельным ионам составит около 760 кДж/моль.
М.Борн предложил схему расчета энергии кристаллической решетки по электростатическому взаимодействию между ионами.
Сила электростатического взаимодействия Fэл. рассчитывается по закону Кулона, который можно записать в следующей форме:
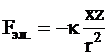 ,
,
где k - константа, включающая диэлектрическую постоянную вакуума, множитель 4p, квадрат заряда электрона, x и z - заряд аниона и заряд катиона в атомных единицах заряда, r - кратчайшее расстояние в кристаллической решетке.
Кроме силы электростатического взаимодействия, между ионами возникает сила отталкивания Fотт., обусловленная взаимодействием электронных оболочек ионов. Ее обычно представляют в виде степенной функции:
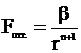 ,
,
где b и n - константы.
Устойчивому состоянию отвечает минимум энергии взаимодействия между ионами, которому соответствует расстояние r = r0, а состоянию разрушенной кристаллической решетки - r = ¥.
Изменение потенциальной энергии dE при изменении расстояния между ионами на dr составит:
du = - (Fэл. + Fотт.)dr,
а энергия удаления ионов из устойчивого состояния на бесконечно большое расстояние окажется равной:
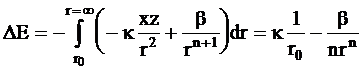 . (3 - 2)
. (3 - 2)
Используя граничные условия r0 = 0, F = 0, находим b:
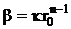 . Следовательно, уравнение (3 - 2) принимает форму:
. Следовательно, уравнение (3 - 2) принимает форму:
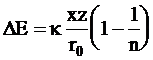 . (3 - 3)
. (3 - 3)
Число соседних ионов противоположного знака у каждого иона определяется типом кристаллической решетки, от которого зависит множитель m, называемый постоянной Маделунга.
В пересчете на 1 моль энергия Гиббса, необходимая для разрушения кристаллической решетки, составит:
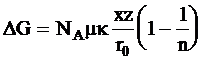 , (3 - 4)
, (3 - 4)
где NA - постоянная Авогадро.
Параметры кристаллической решетки находят по данным рентгеноструктурного анализа. Коэффициент n, учитывающий влияние деформации электронных оболочек на силу отталкивания, оценивают по сжимаемости вещества (12 ³ n ³ 5).
Расчеты энергии кристаллической решетки показывают, что она составляет сотни кДж/моль. Эта величина столь велика, что без дополнительной энергии соединения не смогут существовать в растворах в ионной форме. Источником дополнительной энергии служит энергия, выделяющаяся при сольватации ионов.
Энергия сольватациипредставляет собой изменение энергии Гиббса при внесении из вакуума в данный растворитель 1 моль вещества, взятого в виде отдельных ионов.
Сумма энергии разрушения кристаллической решетки и энергии сольватации представляет собой общее изменение энергии Гиббса, сопровождающее процесс растворения вещества.
В основу расчетов энергии сольватации положены модельные методы.
Первая модель для расчета энергии сольватации была разработана М.Борном.
Процесс сольватации по Борну включает три стадии:
1) разряд ионов, находящихся в вакууме, до нейтральных частиц,
2) внесение незаряженных частиц в растворитель,
3) заряжение нейтральных частиц в растворителе.
Предполагается, что работа на второй стадии равна нулю. Для расчета работы на других стадиях частица рассматривается как шарик. Работа разряжения шарика в вакууме и заряжения его в среде рассчитывается по законам электростатики. Расчет изменения энергии Гиббса при сольватации DGS по модели Борна проводится по следующему уравнению:
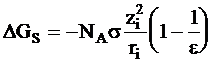 , (3 - 5)
, (3 - 5)
в котором NA - постоянная Авогадро, zi - заряд иона, ri - радиус иона, e - относительная диэлектрическая проницаемость среды, 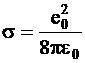 (е0 - заряд электрона, e0 - диэлектрическая проницаемость вакуума).
(е0 - заряд электрона, e0 - диэлектрическая проницаемость вакуума).
Если известна зависимость диэлектрической проницаемости от температуры, то, воспользовавшись уравнением Гиббса - Гельмгольца, можно найти теплоту сольватации:
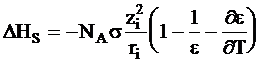 . (3 - 6)
. (3 - 6)
Уравнение (3 - 6) называется уравнением Борна - Бьеррума.
В последующих моделях уточнялось строение сольватных слоев вблизи ионов. В частности, Уэбб ввел поправки на изменение диэлектрической проницаемости среды вблизи иона и на сжатие растворителя под действием электрического поля иона (электрострикции).
Кроме модели Борна - Уэбба, согласно которой растворитель рассматривается как непрерывная среда, были разработаны модели, в которых рассматриваются не отдельные ионы, а их комплексы с растворителем.
В основу ряда моделей положены особые свойства воды. Поэтому такие модели описывают взаимодействие ионов только с водой - гидратацию.
Структура воды является предметом многочисленных исследований.
Геометрия молекулы воды характеризуется следующими данными: расстояние между ядром атома кислорода и ядрами атомов водорода равно 0, 096 нм, а расстояние между ядрами обоих атомов водорода - 0,0141 нм. Две собственных электронных пары атома кислорода и два протона, от которых электронные пары смещены в сторону более электроотрицательного атома кислорода, образуют две пары электрических полюсов. Свободная электронная пара одной молекулы воды и протон другой образуют водородную связь, причем использование всей электронной пары молекулой воды для установления связи усиливает ее акцепторную способность по отношению к электронной паре другой молекулы. Таким образом, водородная связь в воде и водных растворах имеет кооперативный характер. Нейтронографические исследования показали, что кристаллическая структура льда отличается пустотами. В связи с этим молярный объем жидкой воды меньше молярного объема льда. Дж.Бернал и Р.Фаулер предположили, что и в воде молекулы плотно не прилегают друг к другу. Расчеты показывают, что при плотной упаковке молекул плотность воды была бы в 1,8 раз больше обычной. Наличием пустот в жидкой воде объясняется ее аномальный характер: максимум плотности при 4°С, резкий (почти в 2 раза) рост теплоемкости воды по сравнению со льдом, понижение вязкости с ростом давления при температуре 0° – 25°С и др.
Бернал и Фаулер предполагали, что при плавлении воды сохраняются льдоподобные агрегаты, состоящие из нескольких молекул воды. Однако рентгеноструктурный анализ не показал присутствие в жидкой воде льдоподобных областей. Дж.Попл предложил модель, согласно которой водородная связь между молекулами воды может изгибаться (ее также можно рассматривать как своеобразный шарнир). О.Я. Самойлов предположил, что аномальные свойства воды объясняются тем, что плавление льда приводит к заполнению имеющихся в структуре льда пустот свободными молекулами Н2О. Л.Полинг разработал модель, в соответствии с которой молекулы воды как бы покрыты гидратной оболочкой из таких же молекул («гидратная модель»). Кроме того, была предложена модель ассоциатов, объясняющая аномальные свойства воды существованием ассоциатов типа (H2O)x, где х - число ассоциаций (х = 2, 3,... , 8), модель «мерцающих кластеров», по которой образуются короткоживущие ассоциаты - кластеры, отделенные друг от друга мономерными молекулами Н2О, и др. модели.
Влияние ионов на структуру воды связано прежде всего с электростатическим взаимодействием ионов и полярных молекул воды, причем важную роль играет отношение заряда иона к его радиусу. Это объясняется тем, что с увеличением радиуса ионов при постоянном заряде падает условная плотность заряда и снижается поляризующее действие иона. Гидратация ионов, обусловленная электростатическим взаимодействием с полярными молекулами воды, приводит к физической гидратации.
В дополнение к электрическому взаимодействию ионы, имеющие вакантные орбитали, могут образовывать аквакомплексы. Такой способ связывания воды с ионами (обычно переходных металлов) называется химической гидратацией.
Образование слоя молекул воды, непосредственно прилегающих к иону, называется первичной (или ближней) гидратацией. Следующие за первичным слоем молекулы воды участвуютво вторичной (или дальней) гидратации.
Молекулы воды ближнего к иону слоя могут образовывать единый (возможно, короткоживущий) агрегат, участвующий в движении как единое целое. Число таких молекул называют координационным числом гидратации, или числом гидратации.
Экспериментальной базой для изучения гидратации ионов служат подвижность и диффузия ионов, сжимаемость растворов, поглощение ими ультразвука, оптические свойства растворов.
Например, по рентгеноструктурным данным известно, что радиус катионов щелочных металлов возрастает в последовательности Li+< Na+< K+< Cs+, а подвижность ионов изменяется в последовательности Li+< Na+< K+< Cs+. Следовательно, ион лития более гидратирован, чем ион натрия, а ион натрия - более, чем ион калия и т.д. Сжимаемость воды при растворении в ней электролитов снижается. Это явление объясняется сжатием воды в гидратных оболочках под действием электрического поля иона (электрострикцией) и используется для расчета чисел гидратации.
Ван-Аркель и де Бур использовали идею первичной гидратации для введения поправки в уравнение Борна. Они дополнили модель Борна еще одной стадией - гидратацией ионов в газовой фазе.
На основе представлений Бернала и Фаулера была предложена модель, которая включает следующие стадии:
1) удаление ассоциата из воды и перевод его в газовую фазу,
2) разрушение ассоциата,
3) присоединение молекул воды, кроме одной, к иону,
4) возвращение ассоциата с одним ионом и без одной молекулы воды в раствор,
5) возвращение оставшейся молекулы воды в раствор.
