Уравнение однородной линии с распределенными параметрами.

Пусть

Ro , 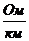- продольное активное сопротивление единицы длины линии;

Lo, - индуктивность единицы длины линии;

Go, 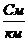- проводимость утечки между проводами из-за несовершенства изоляции на единицу длины;

Co, - емкость между проводами линии на единицу длины;

i– ток в начале участка dx;

- ток в конце участка; приращение обусловлено утечкой через поперечный элемент;

u – напряжение в начале участка dx;

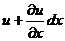- напряжение в конце участка.

На основании уравнений по I и II законам Кирхгофа для участка линии dx после преобразований получим.

По II закону Кирхгофа:

Разделим на dx и преобразуем в вид

(1)

По I закону Кирхгофа:

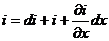
Учитывая, что:

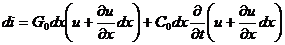
и пренебрегая производной второго порядка, получаем после преобразования

(2)

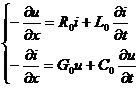- основные дифференциальные уравнения для двухпроводной линии с распределенными параметрами (телеграфные уравнения).

Уравнения однородной линии при установившемся синусоидальном режиме.

Метод Даламбера - S экспонент uп и uo.

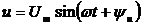
Если ток и напряжение в линии изменяются по синусоидальному закону, то их можно выразить в виде комплексных чисел 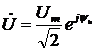и 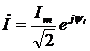. Комплексные 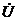и 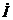зависят только от х, а потому уравнения в частных производных для мгновенных значений u и i переходят в обыкновенные дифференциальные уравнения для 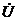и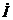

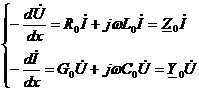(1 и 2)

Первое уравнение полное продольное сопротивление единицы длины, второе уравнение полная поперечная проводимость единицы длины.

Решим полученную систему уравнений относительно 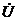и получим

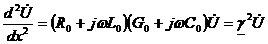(3)

или

где

g - постоянная распространения, (1/км)

a - коэффициент затухания, характеризующий затухание падающей волны на единицу длины линии, (Нп/км)

b - коэффициент фазы, характеризующий изменения фазы падающей волны на единицу длины линии, (рад/км).

Решение линейного дифференциального уравнения (3) второго порядка

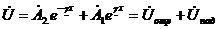(4)

где А1 и А2 – постоянные интегрирования.

Из уравнения (1)

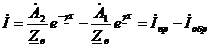(5)

где

- волновое сопротивление, (Ом).

Для постоянного тока (w=0):

;

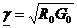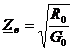
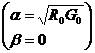
Для линий синусоидального тока без потерь (R0=G0=0)

;

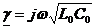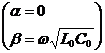
Это метод Даламбера, представленный решением уравнений, как сумму прямых и обратных волн.

Бегущие волны

Выражение для напряжения в любой точке линии (как и для тока) состоит из двух составляющих

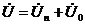или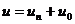

Итак,

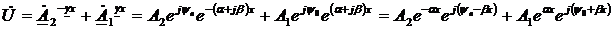
Для перехода от комплекса напряжения к функции времени необходимо умножить правые части формул на 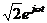и от произведений взять мнимую часть

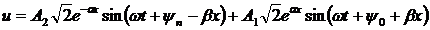
Первая составляющая представляет собой синусоиду, амплитуда которой по мере продвижения вдоль линии от ее начала (линии) уменьшается (затухает) по экспоненциальному закону ( 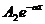), а аргумент этой синусоиды (фазы) является функцией времени и координаты.

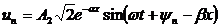
Иначе говоря, с одной стороны, в данной точке линии напряжение un является синусоидальной функцией времени (x=const, t=var).

С другой стороны, в данный момент времени напряжение un будет распределено вдоль линии также по синусоидальному закону.

В целом же, это даст перемещение вдоль линии неизменного фазового состояния напряжения (бегущей волны напряжения) от ее начала к концу с постоянной скоростью называемой фазовой скоростью Uф.

Аналогично образуется бегущая волна тока.

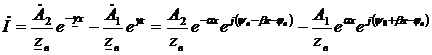
Откуда

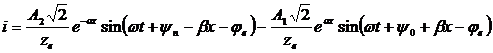
Электромагнитное состояние в любой точке линии определяется совокупностью электрического (волна напряжения) и магнитного (волна тока) полей.

Процесс перемещения электромагнитного состояния (электромагнитной волны) от источника энергии к приемнику, т. е. в нашем случае в сторону (направление) увеличения координаты х, от начала к концу линии называют падающей электромагнитной волной (прямая).

Уменьшение амплитуд падающих волн напряжения и тока по мере их продвижения вдоль линии объясняется наличием потерь в линии (х¹0).

Минимальное расстояние между двумя точками линии (имеющими одну и ту же фазу), фазы напряжения (тока) в которых отличаются на 2p, называется длина волны l.

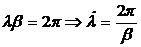
Фазовая скорость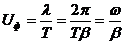

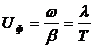
С другой стороны для линии без потерь в вакууме длина волны l равна расстоянию, на которое распространяется бегущая волна за период.

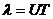, где U=300000 км/с.

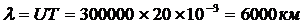
Вторая составляющая

представляет собой синусоиду, амплитуда которой возрастает по экспоненциальному закону при движении от ее начала или, иначе говоря, затухает по мере продвижения от конца к началу.

Процесс перемещения электромагнитного состояния (электромагнитной волны) от приемника к источнику энергии называется отраженной (обратной) электромагнитной волной.

Появление отраженных волн можно рассматривать как результат отражения падающих волн от конца линии.

Коэффициент отражения по напряжению qu – отношение напряжения отраженной волны в конце линии к напряжению падающей волны в конце линии.

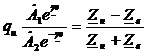
По току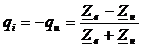

а) Если линия замкнута на конце на сопротивление, равное волновому ( 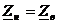), то qu=qi=0, т. е. в линии будут отсутствовать отраженные (обратные) волны. Это согласованный режим работы линии.

б) Если линия на конце разомкнута, т. е. 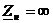, то qu=1 и qi=-1. Следовательно, на конце линии падающая и отраженная волны напряжения равны, в результате напряжение на конце линии в два раза больше падающей волны. Т. к. qi=-1, то результирующий ток равен 0.

в) Если линия закорочена на конце линии, т. е. 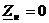, то qu=-1 и qi=1. В результате ток в конце линии равен удвоенному значению тока падающей волны, а напряжение равно 0.