Изучение колебаний математического и физического маятника
Цель работы: изучение колебаний математического и физического маятников и измерение ускорения свободного падения.
Теоретическое введение
 Колебательным движением называется процесс, при котором система, многократно отклоняясь от положения равновесия, каждый раз вновь возвращается к нему.
Колебательным движением называется процесс, при котором система, многократно отклоняясь от положения равновесия, каждый раз вновь возвращается к нему.
Существует общность закономерностей большого разнообразия колебательных процессов, поэтому все они могут быть сведены к совокупности простейших колебаний – гармонических.
Гармоническим колебательным движением называется такое колебательное движение, при котором колеблющаяся величина изменяется с течением времени по закону синуса или косинуса. Основные характеристики колебательных процессов можно рассмотреть на примере механических колебаний материальной точки.
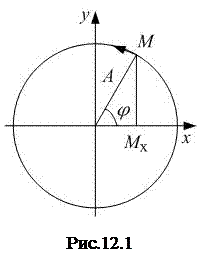
Представим себе материальную точку М, равномерно вращающуюся по окружности радиуса А с угловой скоростью ω (рис.12.1). Тогда точка Мх – проекция точки М на ось х – будет совершать периодические колебания вдоль оси х. Смещение колеблющейся точки от положения равновесия вдоль оси х определяется по закону:
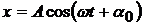 , (12.1)
, (12.1)
где А – амплитуда колебаний (абсолютное значение максимального смещения), 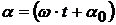 – фаза колебаний, которая определяет угловое смещение точки М в любой момент времени, α0 – начальная фаза,
– фаза колебаний, которая определяет угловое смещение точки М в любой момент времени, α0 – начальная фаза, 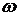 – круговая (циклическая) частота, равная
– круговая (циклическая) частота, равная
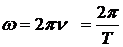 ; (12.2)
; (12.2)
ν – частота колебаний (число полных колебаний в единицу времени,  ,
, 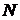 – число колебаний за время t),
– число колебаний за время t),  – период колебаний (время совершения одного полного колебания). Выражение (12.1) – кинематическое уравнение гармонического колебательного движения.
– период колебаний (время совершения одного полного колебания). Выражение (12.1) – кинематическое уравнение гармонического колебательного движения.
 Скорость
Скорость 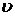 колеблющейся материальной точки получим, продифференцировав (12.1) по времени:
колеблющейся материальной точки получим, продифференцировав (12.1) по времени:
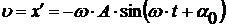 . (12.3)
. (12.3)
Продифференцировав (12.3), получим ускорение а:
 . (12.4)
. (12.4)
Учитывая (12.1), имеем: 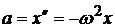 , или:
, или:
 . (12.5)
. (12.5)
Выражение (12.5) описывает гармонические колебания величины x и называется дифференциальным уравнением гармонического осциллятора. Его решением является гармоническая функция (12.1). Если вторая производная по времени какой-либо физической величины (не обязательно смещения) пропорциональна самой величине с противоположным знаком, то данная физическая величина изменяется со временем по гармоническому закону.
Любое тело (рис. 12.2), подвешенное в поле силы тяжести так, что точка подвеса О не совпадает с центром тяжести С, называется физическим маятником. Пусть отклонение маятника от положения равновесия характеризуется углом φ. При отклонении маятника от положения равновесия возникает вращающий момент силы 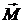 , стремящийся вернуть маятник в положение равновесия. Его величина
, стремящийся вернуть маятник в положение равновесия. Его величина 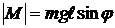 , где m – масса маятника;
, где m – масса маятника;  – расстояние от центра тяжести маятника до точки подвеса,
– расстояние от центра тяжести маятника до точки подвеса, 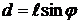 – плечо силы тяжести (кратчайшее расстояние от линии действия силы до оси вращения).
– плечо силы тяжести (кратчайшее расстояние от линии действия силы до оси вращения).
Направления вращающего момента 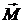 и углового перемещения
и углового перемещения  противоположны (момент силы возвращает маятник к положению равновесия), поэтому в проекциях на ось вращения
противоположны (момент силы возвращает маятник к положению равновесия), поэтому в проекциях на ось вращения
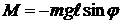 . (12.6)
. (12.6)
По второму закону Ньютона для вращательного движения маятника:
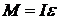 , (12.7)
, (12.7)
где 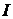 – момент инерции маятника относительно оси, проходящей через точку подвеса; e – угловое ускорение маятника, равное второй производной угла поворота:
– момент инерции маятника относительно оси, проходящей через точку подвеса; e – угловое ускорение маятника, равное второй производной угла поворота: 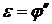 .
.
Из уравнений (12.6) и (12.7) имеем:
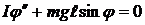 , или
, или 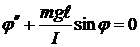 . (12.8)
. (12.8)
При малых углах  , и уравнение (12.8) будет иметь вид:
, и уравнение (12.8) будет иметь вид:
 . (12.9)
. (12.9)
Сравнивая (12.9) и (12.5), устанавливаем, что j изменяется по гармоническому закону с круговой частотой ω, причем
 , (12.10)
, (12.10)
а период колебаний маятника
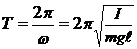 . (12.11)
. (12.11)
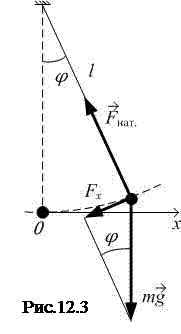
Частным случаем физического маятника является маятник математический. Если вся масса маятника сосредоточена в одной точке (например, шарик, подвешенный на невесомой нерастяжимой нити), то такой маятник называют математическим (рис.12.3). Для математического маятника момент инерции рассчитывается как для материальной точки:  , поэтому период его колебаний равен:
, поэтому период его колебаний равен:
 . (12.12)
. (12.12)
Формулу (12.12) можно получить, непосредственно записав второй закон Ньютона для материальной точки. На шарик, подвешенный на нити (рис.12.3), действуют сила тяжести 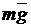 и сила натяжения нити
и сила натяжения нити 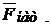 , тогда
, тогда
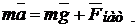 . (12.13)
. (12.13)
Сила натяжения нити 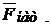 не имеет касательной составляющей, а проекция силы тяжести для малых углов φ равна
не имеет касательной составляющей, а проекция силы тяжести для малых углов φ равна 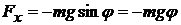 , тогда касательное ускорение
, тогда касательное ускорение  . Угол отклонения маятника из положения равновесия
. Угол отклонения маятника из положения равновесия 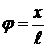 , где x – отклонение из положения равновесия. Наконец, касательное ускорение – это вторая производная координаты x, тогда
, где x – отклонение из положения равновесия. Наконец, касательное ускорение – это вторая производная координаты x, тогда
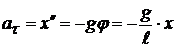 . (12.14)
. (12.14)
Отсюда  . Это дифференциальное уравнение гармонических колебаний идентично (12.5), если
. Это дифференциальное уравнение гармонических колебаний идентично (12.5), если 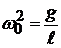 ; следовательно, (12.12) доказано.
; следовательно, (12.12) доказано.
Приведенной длиной физического маятника называется длина такого математического маятника, который имеет тот же период колебаний, что и данный физический маятник:

 . (12.15)
. (12.15)
В лабораторной работе используется физический маятник в виде кольца (рис.12.4) или в виде однородного тонкого стержня (рис.12.5). Момент инерции маятника относительно точки подвеса О можно найти по теореме Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс параллельно данной оси, и произведения массы тела на квадрат расстояния между осями. Для кольца получим:
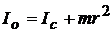 . (12.16)
. (12.16)
Здесь 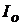 – момент инерции маятника относительно оси, проходящей через точку подвеса O, IC – момент инерции относительно оси, проходящей через центр масс – точку C, r – расстояние между осями. Момент инерции полого (толстостенного) цилиндра или кольца массой m с внутренним радиусом r и наружным R относительно оси, проходящей через центр масс, равен:
– момент инерции маятника относительно оси, проходящей через точку подвеса O, IC – момент инерции относительно оси, проходящей через центр масс – точку C, r – расстояние между осями. Момент инерции полого (толстостенного) цилиндра или кольца массой m с внутренним радиусом r и наружным R относительно оси, проходящей через центр масс, равен:
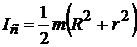 , (12.17)
, (12.17)
Тогда из (12.16) и (12.17) получаем:
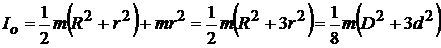 , (12.18)
, (12.18)
где 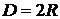 и
и 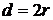 – внешний и внутренний диаметры кольца соответственно. Из (12.11) выразим ускорение свободного падения с учетом, что длина физического маятника равна расстоянию от точки подвеса до центра масс, то есть для кольца
– внешний и внутренний диаметры кольца соответственно. Из (12.11) выразим ускорение свободного падения с учетом, что длина физического маятника равна расстоянию от точки подвеса до центра масс, то есть для кольца  , и из (12.18) подставим момент инерции:
, и из (12.18) подставим момент инерции:
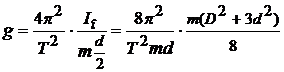 ,
,
и окончательно:
 . (12.19)
. (12.19)
Для стержня по теореме Штейнера получим:
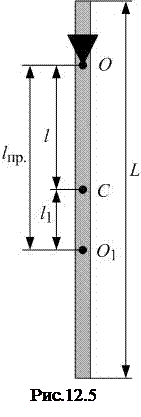
 , (12.20)
, (12.20)
|
|
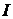 – момент инерции стержня относительно точки подвеса О,
– момент инерции стержня относительно точки подвеса О, 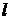 – расстояние между центром масс (центром стержня) и точкой подвеса (длина физического маятника),
– расстояние между центром масс (центром стержня) и точкой подвеса (длина физического маятника),  – момент инерции стержня относительно центра масс:
– момент инерции стержня относительно центра масс:  , (12.21)
, (12.21)
L – длина стержня, m – его масса. Можно показать, что для любого маятника приведенная длина lпр. больше, чем расстояние 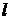 от центра масс до точки подвеса (длины физического маятника): из (12.15) и (12.20) следует, что
от центра масс до точки подвеса (длины физического маятника): из (12.15) и (12.20) следует, что
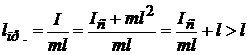 .
.
Точка О1, лежащая на прямой ОС на расстоянии lпр.от точки подвеса маятника (рис.12.5), называется центром качания маятника. Центр качания О1 и точка подвеса О обладают свойством взаимности: если маятник подвесить так, чтобы его ось качания проходила через точку О1, то точка О будет совпадать с новым положением центра качания маятника, то есть приведенная длина и период колебаний маятника останутся прежними. Покажем это. По теореме Штейнера момент инерции I1 маятника относительно оси, проходящей через точку О1, равен:
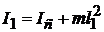 . (12.22)
. (12.22)
Из (12.20) и (12.22) вычислим  :
:
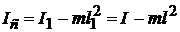 . (12.23)
. (12.23)
Из (12.10) выразим момент инерции маятника  и запишем аналогичную формулу для
и запишем аналогичную формулу для 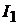 :
: 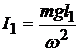 . Здесь использовано условие, что частота колебаний маятника относительно оси, проходящей через точку О1, должна быть той же самой, что и для оси, проходящей через точку О. Подставив оба момента инерции в (12.23) получим уравнение:
. Здесь использовано условие, что частота колебаний маятника относительно оси, проходящей через точку О1, должна быть той же самой, что и для оси, проходящей через точку О. Подставив оба момента инерции в (12.23) получим уравнение:
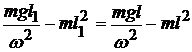 .
.
Далее после преобразований:  ; и после сокращения на
; и после сокращения на 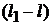 получим:
получим:  . По определению приведенной длины физического маятника (12.15):
. По определению приведенной длины физического маятника (12.15): 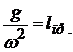 , то есть
, то есть 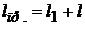 , что и требовалось показать.
, что и требовалось показать.
Для физического маятника – стержня из (12.15), (12.20) и (12.21):
 , или
, или
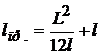 . (12.24)
. (12.24)
Экспериментальная часть
Математический маятник
Примечание: выполнять только по заданию преподавателя.
Приборы и оборудование: секундомер, математический маятник (шарик на нити на штативе).
1. Ознакомьтесь с установкой. Определите длину математического маятника 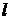 . Отведите маятник от положения равновесия на небольшой угол (10÷150) и отпустите. Пропустив 2-3 колебания, включите секундомер и определите время t, за которое совершится N полных колебаний (взять N=50÷100). Вычислите период колебаний маятника по формуле (12.25):
. Отведите маятник от положения равновесия на небольшой угол (10÷150) и отпустите. Пропустив 2-3 колебания, включите секундомер и определите время t, за которое совершится N полных колебаний (взять N=50÷100). Вычислите период колебаний маятника по формуле (12.25):
 . (12.25)
. (12.25)
Таблица 12.1
| № опыта | 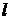 , м , м | 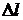 , м , м | N | 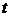 , с , с | 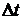 , с , с | 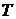 , с , с |  , с , с | 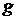 , м/с2 , м/с2 | 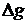 , м/с2 , м/с2 |  , % , % | 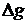 , м/с2 , м/с2 |
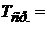 |  |  |  | ||||||||
 | 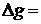 |
2. Повторите опыт (можно установить другую длину маятника) не менее 3 раз. Вычислите значение ускорения свободного падения по формуле (12.26):
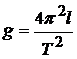 . (12.26)
. (12.26)
3. Рассчитайте погрешности измерений.
4. Все результаты занесите в таблицу 12.1.
Замечание: Среднее значение периода 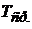 рассчитывается только в том случае, если длина маятника одна и та же во всех опытах. Тогда ускорение свободного падения
рассчитывается только в том случае, если длина маятника одна и та же во всех опытах. Тогда ускорение свободного падения 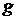 следует рассчитать один раз, исходя из среднего значения периода. В этом случае погрешность периода рассчитывается по стандартной методике расчета погрешностей случайной величины:
следует рассчитать один раз, исходя из среднего значения периода. В этом случае погрешность периода рассчитывается по стандартной методике расчета погрешностей случайной величины:
 , (12.27)
, (12.27)
где n – число опытов,  – абсолютная погрешность i-го опыта,
– абсолютная погрешность i-го опыта, 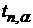 – коэффициент Стьюдента для доверительной вероятности α=0.95.
– коэффициент Стьюдента для доверительной вероятности α=0.95.
Далее погрешность 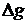 рассчитывается по стандартной методике для расчета погрешностей при косвенных измерениях:
рассчитывается по стандартной методике для расчета погрешностей при косвенных измерениях:
 . (12.28)
. (12.28)
Если длина маятника в опытах была неодинаковой, ускорение свободного падения 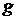 рассчитывается в каждом опыте, затем усредняется, и его погрешность рассчитывается как при прямых измерениях случайной величины, то есть по формуле, аналогичной (12.27):
рассчитывается в каждом опыте, затем усредняется, и его погрешность рассчитывается как при прямых измерениях случайной величины, то есть по формуле, аналогичной (12.27):
 .
.
Физический маятник – кольцо (обруч).
Приборы и оборудование: секундомер, физический маятник (кольцо или обруч на штативе с опорной призмой), линейка, штангенциркуль.
1. Измерьте внешний 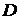 и внутренний диаметр
и внутренний диаметр 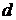 кольца.
кольца.
2. Определите при помощи секундомера время 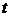 , за которое совершится N полных колебаний (N=30÷50). Вычислите период колебаний по формуле (12.25).
, за которое совершится N полных колебаний (N=30÷50). Вычислите период колебаний по формуле (12.25).
3. Повторите опыт не менее 3 раз (оптимально – 5).
4. Определите ускорение свободного падения по формуле (12.19), подставив в неё среднее значение периода колебаний.
5. Определите погрешность измерений:
 , где производные равны:
, где производные равны:
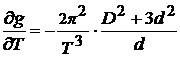 ;
; 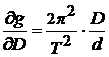 ;
; 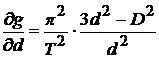 .
.
6. Все результаты измерений и вычислений занесите в таблицу 12.2.
Таблица 12.2
| № | 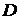 , м , м |  , м , м | 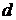 , м , м | 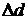 , м , м | N | 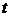 , с , с | 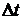 , с , с | 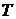 , с , с |  , с , с |  | 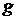 , м/с2 , м/с2 | 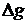 , м/с2 , м/с2 |  |
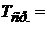 |  |
Физический маятник – стержень
Приборы и оборудование: секундомер, физический маятник (стержень с опорной призмой), штатив, линейка.
1. Измерьте длину стержня  .
.
2. Измерьте 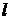 – расстояние от точки подвеса стержня до его центра. Величина
– расстояние от точки подвеса стержня до его центра. Величина 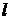 не должна быть меньше 13 см.
не должна быть меньше 13 см.
3. Определите при помощи секундомера время t, за которое совершится N полных колебаний (30÷50). Вычислите период колебаний по формуле (12.25).
4. Повторите опыт 5 раз.
5. Рассчитайте погрешность периода по формуле (12.27).
6. Определите экспериментальное значение приведенной длины физического маятника (см. (12.15)), используя среднее значение периода колебаний:
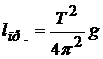 . (12.29)
. (12.29)
7. Рассчитайте погрешность приведенной длины:
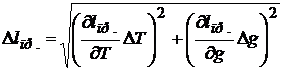
8. Найдите точку качания физического маятника; для этого нужно вычислить l1=lпр–l и закрепить опорную призму маятника на расстоянии l1 от центра стержня.
9. Повторите измерения времени t1 для N колебаний и расчеты периода T1 и его погрешности (пункты 3-5). Результаты запишите в таблицу 12.3.
10. Сравните T1 и T, сделайте выводы.
11. По формуле (12.24) определите lпр.теор. – теоретическое значение приведенной длины, рассчитайте погрешность:
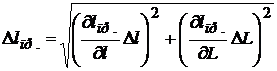 ,
,
где производные равны 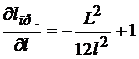 ;
;  (см. (12.24)).
(см. (12.24)).
12. Все полученные данные запишите в табл.12.3.
13. Сравните теоретическое и экспериментальное значения lпр, сделайте выводы.
Таблица 12.3
| № |  , м , м | 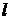 , м , м | N | 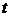 , с , с | 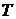 , с , с |  , с , с |  , с , с | 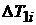 i, с i, с | lпр., м | Δlпр., м | lпр. теор. | Δlпр. теор. |
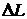 = = | 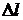 = = | Tср.= |  | T1ср.= |  | |||||||
 |  |
Контрольные вопросы
1. Дайте определение колебательного процесса.
2. Какие колебания называются гармоническими?
3. Выведите дифференциальное уравнение гармонических колебаний.
4. Что называется математическим маятником?
5. Дайте определение физического маятника.
6. Что называется угловым ускорением?
7. Дайте определение момента инерции твердого тела.
8. Что такое момент силы?
9. Сформулируйте основной закон динамики вращательного движения.
10. Получите дифференциальное уравнение колебаний физического маятника.
11. Получите формулу для круговой частоты и периода колебаний физического маятника.
12. Сформулируйте теорему Штейнера. Как в данной работе она используется?
13. Что такое приведенная длина физического маятника?
14. Как найти период и частоту колебаний математического маятника?
15. Выведите формулу (12.19).
16. Что такое точка качания? Чем она замечательна?
Используемая литература
[5] §2.8, 7.1, 7.3, 19.1, 19.2; [3] §4.1, 4.2, 4.3, 27.1, 27.2; [1] §38, 39, 49, 50, 53, 54; [6] §3.3; 3.6, 3.7, 3.8; [7] §16, 18, 140, 141, 142.
Лабораторная работа 1-13
