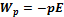Напряженность поля. Потенциал.

Потенциал – это скалярная физическая величина, численно равная потенциальной энергии единичного положительного заряда в данной точке пространства (фи = W/q). За нулевой потенциал часто удобно принимать потенциал бесконечно удаленной точки пространства.

В потенциальном поле тела обладают потенциальной энергией и работа консервативных сил совершается за счет убыли потенциальной энергии A12=W1-W2.

Разностью потенциалов между точками 1 и 2 называется работа, совершаемая силами поля при перемещении единичного положительного заряда по произвольному пути из точки 1 и в точку 2: (фи1-фи2=А12/q)

dA=qEdl

dA=-qdфи=-q(бфи/бl)dl (б - частная производная, а Лосев - лох=)))

напряженность электростатического поля равна градиенту потенциала, взятому с обратным знаком (Е=-grad фи=-(rot,вект) фи)

эквипотенциальные поверхности – поверхности, во всех точках которых потенциал имеет одно и то же значение.

3.Энергия взаимодействия системы зарядов.

Физики проверили точность, с которой специальная теория относительности (СТО) Эйнштейна предсказывает релятивистское замедление времени. Эксперимент - самый точный из проводившихся когда-либо в этой области - показал, что погрешность составляет менее одной десятимиллионной секунды, сообщает журнал Science.
Эффект релятивистского замедления времени можно описать примерно следующим образом: представим себе, что наблюдатель А неподвижен, а наблюдатель Б движется относительного него.
С точки зрения наблюдателя А, часы наблюдателя Б идут медленнее, чем его собственные часы.
Замедление времени начинает становиться значительным только при скоростях, сравнимых со скоростью света.

Согласно СТО время в движущейся системе течет медленнее, чем в неподвижной:

Тогда частота колебаний (безразлично каких) в движущейся системе (измеренная неподвижным наблюдателем) будет меньше, чем в неподвижной:

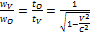или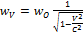

, где - частота колебаний в движущейся системе, а - в неподвижной. Таким образом, измеряя частоту излучения, пришедшего к неподвижному наблюдателю из движущейся системы, по отношению частот можно вычислить скорость системы.

Тепреь вспомним приведенную в статье «Кратко о силовом взаимодействии движущихся зарядов или неожиданное появление коэффициента β» формулу для «релятивистского» закона Кулона:

, где - «релятивистская длина». Или 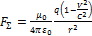. То есть Кулонова сила уменьшается при увеличении скорости.

4.Связь между напряженностью электрического поля и потенциалом.

dA=qEdl

dA=-qdфи=-q(бфи/бl)dl (б - частная производная, а Лосев - лох=)))

напряженность электростатического поля равна градиенту потенциала, взятому с обратным знаком (Е=-grad фи=-(rot,вект) фи)

эквипотенциальные поверхности – поверхности, во всех точках которых потенциал имеет одно и то же значение.

Диполь.

Электрическим диполем называется система двух одинаковых по величине разноимённых точечных зарядов +q и –q, на расстоянии l между которыми значительно меньше расстояния до тех точек, в которых определяется поля системы. Прямая, проходящая через оба заряда, называется осью диполя.

Поле диполя обладает осевой симметрией. Поэтому вид поля в любой плоскости, проходящей через ось диполя, будет одной и той же, причём вектор E лежит в этой плоскости. Потенциал в точке, опред.рад.вектором:

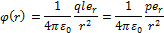
Где — характеристика диполя, называется его электрическим моментом. Вектор р направлен по оси диполя от отрицательного заряда к положительному.

Рассмотрим поведение диполя во внешнем эл.поле. Если диполь поместить в однородное эл.поле, образующие диполь заряды +q и –q окажутся под действием равных по величине, но противоположных по направлению сил . Эти силы образуют пару, плечо которой равно l·sinα, т.е. зависит от положения диполя относительно поля, также они стремится повернуть диполь так, чтобы электрический момент диполя развернулся вдоль направления поля.

Величина момента пары сил: , .

Момент сил стремится развернуть диполь вдоль силовой линии электрического поля.

Во внешнем неоднородном поле силы, действующие на концы диполя, неодинаковы.

Их результирующая сила стремится передвинуть диполь. Диполь втягивается в область поля с большей напряженностью, если угол альфа

меньше пи/2. При альфа больше меньше пи/2 диполь будет выталкиваться из области более сильного поля. энергия диполя во внешнем поле

W = q*(фи(+)-фи(-))

фи(+)-фи(-)=-El => W = -p*E

Потенциальная энергия, которой обладает диполь во внешнем электрическом поле: