Электрический заряд. Закон Кулона.

Электрический заряд. Закон Кулона.

Сила взаимодействия между двумя частицами, находящимися в вакууме и имеющими заряды q₁ и q₂, можетбыть определена из следующей формулы:

Электрический заряд – это внутреннее свойство тел или частиц, характеризующее их способность к электромагнитным взаимодействиям.

Существует элементарный (минимальный) электрический заряд e=1,6*10-19 Кл. Носитель элементарного отрицательного заряда – электрон.

свойства:

1. Электрический заряд существует в двух видах: положительном и отрицательном. Одноименные заряды притягиваются, разноименные – отталкиватся.

2. Электрический заряд инвариантен – его величина не зависит от системы отсчета и, следовательно, не зависит от того движется он или покоится.

3. Электрический заряд дискретен – заряд любого тела составляет целое кратное элементарного электрического заряда е.

4. Электрический заряд аддитивен – заряд любой системы тел (частиц) равен сумме зарядов тел (частиц), входящих в систему.

Точечный электрический заряд – это заряженная материальная точка.

закон взаимодействия двух точеных зарядов (закон Кулона):

сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, прямо пропорциональна величинам зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль соединяющей их прямой

результирующая сила с которой действуют одни заряды на другой, определяется по принципу суперпозиции сил (F=сигмаFi)

Напряженность – (силовая векторная характеристика электростатического поля)это сила, действующая на единичный положительный неподвижный заряд, помещеный в данную точку. (E = F/q)

принцип суперпозиции электрических полей:

напряженность электрического поля системы точечных зарядов равна векторной сумме напряженностей полей каждого из этих зарядов в отдельности

Диполь.

Электрическим диполем называется система двух одинаковых по величине разноимённых точечных зарядов +q и –q, на расстоянии l между которыми значительно меньше расстояния до тех точек, в которых определяется поля системы. Прямая, проходящая через оба заряда, называется осью диполя.

Поле диполя обладает осевой симметрией. Поэтому вид поля в любой плоскости, проходящей через ось диполя, будет одной и той же, причём вектор E лежит в этой плоскости. Потенциал в точке, опред.рад.вектором:

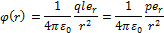
Где — характеристика диполя, называется его электрическим моментом. Вектор р направлен по оси диполя от отрицательного заряда к положительному.

Рассмотрим поведение диполя во внешнем эл.поле. Если диполь поместить в однородное эл.поле, образующие диполь заряды +q и –q окажутся под действием равных по величине, но противоположных по направлению сил . Эти силы образуют пару, плечо которой равно l·sinα, т.е. зависит от положения диполя относительно поля, также они стремится повернуть диполь так, чтобы электрический момент диполя развернулся вдоль направления поля.

Величина момента пары сил: , .

Момент сил стремится развернуть диполь вдоль силовой линии электрического поля.

Во внешнем неоднородном поле силы, действующие на концы диполя, неодинаковы.

Их результирующая сила стремится передвинуть диполь. Диполь втягивается в область поля с большей напряженностью, если угол альфа

меньше пи/2. При альфа больше меньше пи/2 диполь будет выталкиваться из области более сильного поля. энергия диполя во внешнем поле

W = q*(фи(+)-фи(-))

фи(+)-фи(-)=-El => W = -p*E

Потенциальная энергия, которой обладает диполь во внешнем электрическом поле: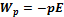

Теорема Гаусса

Теорема Гаусса — основная теорема электродинамики, которая применяется для вычисления электрических полей. Она выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченной этой поверхностью.

Поток вектора напряжённости электрического поля через любую, произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

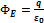, где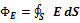

Для теоремы Гаусса справедлив принцип суперпозиции, то есть поток вектора напряжённости через поверхность не зависит от распределения заряда внутри поверхности.

Для поля в веществе электростатическая теорема Гаусса может быть записана иначе — через поток вектора электрического смещения (электрической индукции). При этом формулировка теоремы выглядит следующим образом: поток вектора электрического смещения через замкнутую поверхность пропорционален заключённому внутри этой поверхности свободному электрическому заряду:

Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

B природе не существует «магнитных зарядов», которые создавали бы магнитное поле, как электрические заряды создают электрическое поле. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является вихревым.

Рассмотрим поле, создаваемое бесконечной однородной заряженной плоскостью. Пусть поверхностная плотность заряда плоскости одинакова и равна 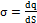. Представим себе мысленно цилиндр с образующими, перпендикулярными к плоскости, и основанием ΔS, расположенным относительно плоскости симметрично. В силу симметрии E' = E'' = E. Поток вектора напряжённости равен 2EΔS.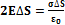

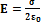
Рассмотрим поле, создаваемое бесконечной нитью. Определим напряжённость, создаваемую этим полем на расстоянии R от нити. Возьмём цилиндр с осью, совпадающей с нитью, радиусом R и высотой Δl. Тогда поток напряжённости через эту поверхность рассчитывается следующим образом: ;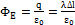

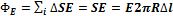
Вектор эл.смещения

ВЕКТОР ЭЛЕКТРИЧЕСКОГО СМЕЩЕНИЯ (Д), ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ (e), ЭНЕРГИЯ ПОЛЯ (W)

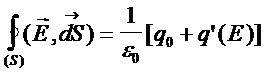
Если электрическое поле имеет место в диэлектрике, то наблюдается поляризация вещества и появляются связанные электрические заряды.

Учитывают поляризацию с помощью вектора поляризации , который для анизотропных и однородных сред выражается через напряженность поля следующим образом: , где c – диэлектрическая восприимчивость вещества (диэлектрика). Вектор поляризации равен также поверхностной плотности связанных зарядов, возникающих в диэлектрике под воздействием внешнего электрического поля (Р = sсвяз ).

Кроме этого, при анализе электростатических полей используют вектор электрического смещения:

Единицей электрического смещения является кулон на метр квадратный (Кл/м2).

Величина e = e0 + c является основной характеристикой диэлектрика и называется абсолютной диэлектрической проницаемостью. Отношение er = e/e0 называют относительной диэлектрической проницаемостью.

Сила Лоренца. Сила Ампера.

Сила ампера:

Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположном — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила , с которой магнитное поле действует на элемент объёма dV проводника с током плотности , находящегося в магнитном поле с индукцией :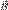

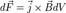
Элементарную силу взаимодействия 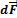между элементами и 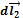проводников, по которым протекают токи I₁ и I₂ можно определить из закона Ампера:

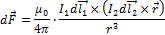
Сила Лоренца:

Выражение для силы, с которой магнитное поле действует на движущийся заряд, впервые получил голландский физик Хендрик Антон Лоренц (1895 г.). В его честь эта сила называется силой Лоренца.

Сила Лоренца — это сила, с которой магнитное поле действует на движущуюся в нем заряженную частицу.

Модуль силы Лоренца равен произведению модуля индукции магнитного поля B(вектор), в котором находится заряженная частица, модуля заряда q этой частицы, ее скорости υ и синуса угла между направлениями скорости и вектора индукции магнитного поля

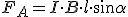
Для определения направления силы Лоренца применяют правило левой руки: если левую руку расположить так, чтобы вектор индукции магнитного поля ( 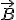) входил в ладонь, четыре вытянутых пальца указывали направления скорости движения положительно заряженной частицы ( 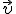), тогда отогнутый на 90° большой палец укажет направление силы Лоренца ( 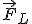) (рис. 3, а). Для отрицательной частицы четыре вытянутых пальца направляют против скорости движения частицы (рис. 3, б).

Поскольку величина B∙sin α представляет собой модуль компоненты вектора индукции, перпендикулярной скорости заряженной частицы, 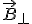, то ориентацию ладони можно определять именно этой компонентой — перпендикулярная составляющая к скорости заряженной частицы должна входить в открытую ладонь левой руки.

Так как сила Лоренца перпендикулярна вектору скорости частицы, то она не может изменить значение скорости, а изменяет только ее направление и, следовательно, не совершает работы.

Намагничение магнетика

Степень намагничивания хар-ся намагниченностью J - магнитным моментом единицы объема:

J=(1/дельтаV)*сумма(pm) или J=n<pm>, где n-концентрация молекул

Т о циркуляции в-ра намагниченности J:

цирк. J по произв. замкн. к-ру L равна алгебр. сумме токов намагнич. I', охв. контуром

где I'=интегр.j'*dS

В дифф. форме: rotJ=j' - ротор в-ра намагниченности равен плотности тока намагн. в этой точке

Напряженность магнитного поля H=B/мю0-J

[H]=1 А/м

Вихревое электрическое поле

Если провод неподвижен, а магнитное поле переменное, то в пространстве (в проводнике, в частности) возникает особое электрическое поле, называемое вихревым электрическим полем. Оно было открыто теоретически Максвеллом. Вихревое электрическое поле отличается от электростатического (потенциального) следующими свойствами: источником поля служат не заряды, а магнитное поле; в вихревом электрическом поле силовые линии – замкнутые, а работа по перемещению заряда по замкнутой линии не равна нулю.

Рассмотрим подробнее вихревое электрическое поле на следующем примере. Пусть однородное переменное магнитное поле с индукцией B(t) создается внутри длинного соленоида С, по проводам которого протекает переменный ток. В этом поле находится неподвижное проволочное кольцо К радиусом r и площадью S. Линии магнитной индукции направлены вдоль оси соленоида и перпендикулярны плоскости кольца. Согласно, в кольце возникает ЭДС индукции.

Вследствие осевой симметрии, замкнутые линии напряженности вихревого электрического поля представляют собой окружности. Вектор E направлен по касательной к окружности, а его модуль E постоянен на данной окружности. На заряд q в кольце действует сила qE, которая при перемещении заряда по кольцу длиной L совершает стороннюю работу.

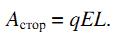
Следовательно, ЭДС в кольце равна произведению напряженности вихревого электрического поля на длину кольца =>

Если ток в соленоиде изменяется по гармоническому закону с циклической частотой ω (ω = 2πν = 2π/T), то и магнитная индукция будет изменяться с такой же частотой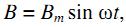

где B_m – максимальное значение (амплитуда). Тогда dB/dt = ωBm cos ωt. Для нахождения напряженности вихревого электрического поля на расстоянии r от оси соленоида подставим в L =2πr и S = πr², тогда 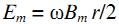представляет амплитуду электрического поля.

Напряженность вихревого электрического поля пропорциональна частоте тока. Она может достигать больших значений в магнитных полях, создаваемых токами высокой частоты радиодиапазона.

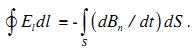является основным уравнением Максвелла и выражает важнейшее свойство электромагнитного поля: в переменном магнитном поле возникает вихревое электрическое поле.

28. ТОК СМЕЩЕ́НИЯ

В соответствии с теорией Максвелла, в цепи переменного тока, содержащей конденсатор, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, какое создавал бы ток, (названный током смещения), если бы он протекал между обкладками конденсатора. Из этого определения следует, что J_D = J (т. е., численные значения плотности тока проводимости и плотности тока смещения равны), и, следовательно, линии плотности тока проводимости внутри проводника непрерывно переходят в линии плотности тока смещения между обкладками конденсатора. Плотность тока смещения j_см характеризует скорость изменения электрической индукции D во времени:

Ток смещения не выделяет джоулевой теплоты, его основное физическое свойство — способность создавать в окружающем пространстве магнитное поле.

Вихревое магнитное поле создается полным током, плотность которого j, равна сумме плотности тока проводимости и тока смещения. Именно поэтому для этой величины и было введено название ток.

Уравнения Максвелла

Уравнения Максвелла - уравнения классической электродинамики, описывающие динамику электромагнитного поля и его связь с зарядами и токами. Уравнения Максвелла явились теоретическим обобщением экспериментальных законов: Кулона, Ампера, законов электромагнитной индукции и других.

Уравнения Максвелла в гауссовой системе единиц имеют вид

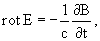div B = 0,

div D = 4πρ,

где E - напряжённость электрического поля, H - напряжённость магнитного поля, D - электрическая индукция, B - магнитная индукция, ρ - плотность электрического заряда, j - плотность электрического тока.

Для того, чтобы использовать уравнения Максвелла для решения задач электродинамики в различных средах, необходимо учесть индивидуальные свойства среды.

D = εE, B = μH,

ε - диэлектрическая проницаемость среды, μ - магнитная проницаемость среды, σ - электропроводность среды. В вакууме без зарядов и токов

D = ε₀E, B = μ₀H,

div E = 0, div H = 0,

Эта система дифференциальных уравнений имеет решение - гармоническую плоскую волну. Векторы электрического и магнитного полей перпендикулярны направлению распространения волны и друг другу и находятся в фазе. Волна распространяется со скоростью.

c = (μ₀ε₀)^-1/2.

c - скорость света в вакууме, c = 2.99792458·10⁸ м/с,

ε₀ - электрическая постоянная, ε₀ = 8.85418782·10^-12 Ф/м,

μ₀ - магнитная постоянная, μ₀ = 1.25663706·10^-6 Гн/м.

Электрический заряд. Закон Кулона.

Сила взаимодействия между двумя частицами, находящимися в вакууме и имеющими заряды q₁ и q₂, можетбыть определена из следующей формулы:

Электрический заряд – это внутреннее свойство тел или частиц, характеризующее их способность к электромагнитным взаимодействиям.

Существует элементарный (минимальный) электрический заряд e=1,6*10-19 Кл. Носитель элементарного отрицательного заряда – электрон.

свойства:

1. Электрический заряд существует в двух видах: положительном и отрицательном. Одноименные заряды притягиваются, разноименные – отталкиватся.

2. Электрический заряд инвариантен – его величина не зависит от системы отсчета и, следовательно, не зависит от того движется он или покоится.

3. Электрический заряд дискретен – заряд любого тела составляет целое кратное элементарного электрического заряда е.

4. Электрический заряд аддитивен – заряд любой системы тел (частиц) равен сумме зарядов тел (частиц), входящих в систему.

Точечный электрический заряд – это заряженная материальная точка.

закон взаимодействия двух точеных зарядов (закон Кулона):

сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, прямо пропорциональна величинам зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль соединяющей их прямой

результирующая сила с которой действуют одни заряды на другой, определяется по принципу суперпозиции сил (F=сигмаFi)

Напряженность – (силовая векторная характеристика электростатического поля)это сила, действующая на единичный положительный неподвижный заряд, помещеный в данную точку. (E = F/q)

принцип суперпозиции электрических полей:

напряженность электрического поля системы точечных зарядов равна векторной сумме напряженностей полей каждого из этих зарядов в отдельности