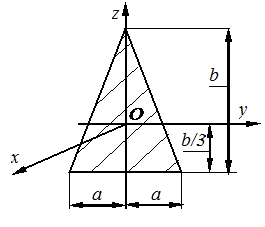
Осевые моменты инерции однородных пластинок
| Форма пластинки | 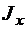 | 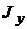 |  |
 | 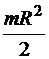 |  |  |
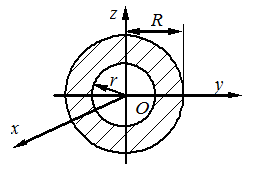 | 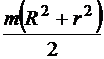 |  |  |
 | 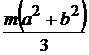 |  | 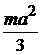 |
 | 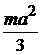 | 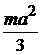 | |
 |  |  | 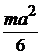 |
4.3. Пример выполнения задания
4.3.1. Условие примера
Тело D, имеющее форму прямоугольной пластины, показанной на рис. 4.2, массой 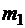 =20 кг вращается вокруг вертикальной оси z с угловой скоростью
=20 кг вращается вокруг вертикальной оси z с угловой скоростью 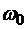 =2 с-1. При этом в точке M желоба AB тела D на расстоянии ÈAM=
=2 с-1. При этом в точке M желоба AB тела D на расстоянии ÈAM=  от точки A, отсчитываемом вдоль желоба, закреплена материальная точка K массой
от точки A, отсчитываемом вдоль желоба, закреплена материальная точка K массой  =8 кг. В момент времени
=8 кг. В момент времени 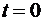 на систему начинает действовать пара сил с моментом
на систему начинает действовать пара сил с моментом  Нм. При t=t1=4 с действие пары сил прекращается; одновременно точка K начинает относительное движение по желобу согласно закону
Нм. При t=t1=4 с действие пары сил прекращается; одновременно точка K начинает относительное движение по желобу согласно закону  м.
м.
Определить угловые скорости тела D соответственно в моменты времени 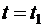 и t=t2=5 с, если R=0,6 м, a=1,2 м; b=0,9 м
и t=t2=5 с, если R=0,6 м, a=1,2 м; b=0,9 м

4.3.2. Решение примера
Запишем равенство, выражающее теорему об изменении кинетического момента механической системы относительно оси z
 , (4.1)
, (4.1)
где  - кинетический момент механической системы, состоящей в данном случае из кинетического момента тела D и кинетического момента точки К, относительно оси z;
- кинетический момент механической системы, состоящей в данном случае из кинетического момента тела D и кинетического момента точки К, относительно оси z;
 - главный момент внешних сил, приложенных к системе, относительно оси z.
- главный момент внешних сил, приложенных к системе, относительно оси z.
Рассмотрим движение системы в отрезке времени [0;t1].
В произвольный момент времени на систему действуют внешние силы 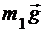 ,
,  ,
,  ,
,  ,
,  ,
, 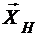 ,
, 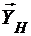 ,
,  (рис. 4.3), главный момент которых относительно оси z равен вращающему моменту
(рис. 4.3), главный момент которых относительно оси z равен вращающему моменту 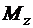 , то есть
, то есть
 . (4.2)
. (4.2)

Кинетический момент данной системы равен сумме
 ,
,
где 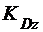
 - кинетические моменты тела D и точки K относительно оси z.
- кинетические моменты тела D и точки K относительно оси z.
Тело D вращается относительно неподвижной оси, поэтому
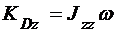 .
.
Здесь  - угловая скорость тела, а
- угловая скорость тела, а 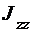 - его момент инерции относительно оси z.
- его момент инерции относительно оси z.
Момент инерции 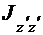 тела относительно оси
тела относительно оси  , параллельной оси z и проходящей через центр масс О тела, определяется по формуле (табл. 4.2)
, параллельной оси z и проходящей через центр масс О тела, определяется по формуле (табл. 4.2)
 .
.
По теореме Штейнера
 .
.
Таким образом
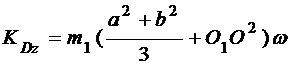 .
.
Кинетический момент материальной точки K, закрепленной в точке М желоба
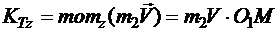 .
.
Скорость точки К
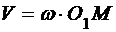 .
.
Очевидно, что  .
.
Согласно условию задачи длина дуги окружности  , тогда центральный угол
, тогда центральный угол  . Следовательно, в равнобедренном треугольнике ОМО1
. Следовательно, в равнобедренном треугольнике ОМО1 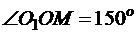 и
и  .
.
Имеем
 .
.
Окончательное выражение кинетического момента системы относительно оси z следующее
 (4.3)
(4.3)
Подставляя выражения (4.2) и (4.3) в равенство (4.1), имеем
 ,
,
откуда
 .
.
Разделяем в последнем уравнении переменные и интегрируем левую и правую части уравнения:
 .
.
Тогда
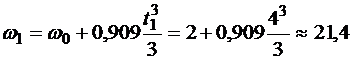 с-1.
с-1.
В момент времени t1 из выражения (4.3) имеем
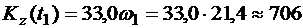 Нмс.
Нмс.
Рассмотрим теперь движение системы в отрезке времени 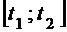 .
.
После прекращения действия момента  на тело D, главный момент внешних сил относительно оси z
на тело D, главный момент внешних сил относительно оси z  (см. рис. 4.4).
(см. рис. 4.4).
Тогда равенство (4.1) примет вид
 ,
,
то есть 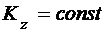 .
.
Это означает, что кинетические моменты системы относительно оси в начале t1 и в конце t2 отрезка времени [t1; t2] равны
 .
.

В момент времени t2 тело D вращается с угловой скоростью  (см. рис. 4.4). При этом точка К, совершая сложное движение, оказывается в точке В желоба. Действительно, центральный угол
(см. рис. 4.4). При этом точка К, совершая сложное движение, оказывается в точке В желоба. Действительно, центральный угол
 .
.
Кинетический момент системы 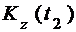 относительно оси в конце t2 отрезка времени [t1; t2] также равен сумме кинетических моментов тела
относительно оси в конце t2 отрезка времени [t1; t2] также равен сумме кинетических моментов тела 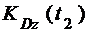 и точки
и точки  :
:
 .
.
Очевидно, что
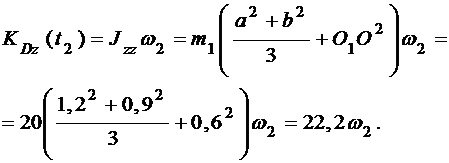
По теореме о сложении скоростей:
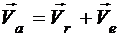 ,
,
где  ,
, 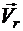 ,
, 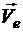 - абсолютная, относительная и переносная скорости точки.
- абсолютная, относительная и переносная скорости точки.
Умножая обе части этого равенства на m2, получаем:
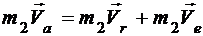 .
.
Следовательно, кинетический момент точки К в конце отрезка времени t2 равен сумме моментов векторов  и
и  относительно оси z
относительно оси z
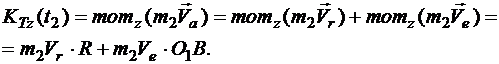
Относительная скорость точки К
 .
.
При t=t2=5 c найдем величину относительной скорости точки К
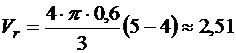 м/с.
м/с.
Переносная скорость точки К
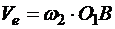 .
.
Из прямоугольного треугольника О1ОВ по теореме Пифагора имеем:
 .
.
Окончательно получаем

Тогда
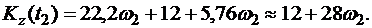
Приравнивая 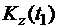 и
и  :
:
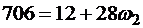 ,
,
находим
 с-1.
с-1.
5. Задание №4. Применение теоремы об изменении
кинетической энергии к изучению движения механической системы
5.1. Содержание задания
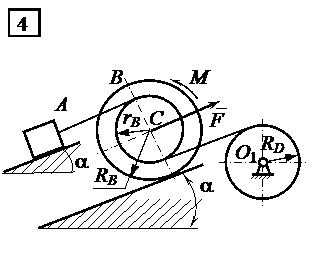
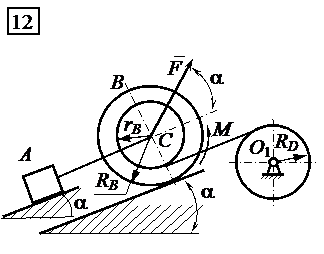
Механическая система, изображенная на рис. 5.1, приводится в движение из состояния покоя. При этом колесо В катится без скольжения по плоскости. Массы тел А, В и D (  ,
,  ,
, 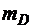 ), заданная нагрузка (
), заданная нагрузка (  и
и 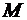 ) приведены в табл. 5.1. Радиусы колеса В и блока D соответственно равны
) приведены в табл. 5.1. Радиусы колеса В и блока D соответственно равны 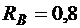 м,
м, 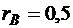 м,
м,  м. Радиус инерции колеса В:
м. Радиус инерции колеса В:  м. Углы
м. Углы 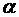 и
и  имеют значения:
имеют значения: 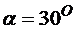 ,
,  . Коэффициент трения качения колеса В равен
. Коэффициент трения качения колеса В равен 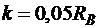 ; коэффициент трения скольжения тела А равен
; коэффициент трения скольжения тела А равен  .
.
Используя теорему об изменении кинетической энергии системы, определить скорость и ускорение тела А после того, как оно переместится на расстояние 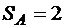 м. Блок D считать однородным сплошным диском; силами сопротивления движению, трением в подшипниках, массой троса, его растяжением и проскальзыванием по ободу блока пренебречь.
м. Блок D считать однородным сплошным диском; силами сопротивления движению, трением в подшипниках, массой троса, его растяжением и проскальзыванием по ободу блока пренебречь.
5.2. Краткие указания к выполнению задания
5.2.1. Прежде, чем приступить к выполнению задания, необходимо проработать соответствующие разделы лекций и рекомендуемой литературы [1 – 4].
5.2.2. Записать равенство, выражающее теорему об изменении кинетической энергии механической системы.
5.2.3. Записать выражения кинетической энергии механической системы в начальном и конечном положениях, как функции искомой скорости тела А.
5.2.4. Определить суммарную работу внешних и внутренних сил на перемещениях их точек приложения при переходе системы из начального положения в конечное и выразить ее в зависимости от перемещения тела А.
5.2.5. Определить скорость и ускорение тела А.
Таблица 5.1
Варианты числовых значений параметров задания №4
| № Вар. | № Подвар. | № Дан. |  , кг , кг |  , кг , кг | 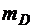 , кг , кг | M, Hм | F, Н |
| 1. | 0,5 | ||||||
| 0,4 | |||||||
| 0,6 | |||||||
| 0,3 | |||||||
| 0,7 | |||||||
| 0,2 | |||||||
| 2. | 0,8 | ||||||
| 0,5 | |||||||
| 0,4 | |||||||
| 0,3 | |||||||
| 0,6 | |||||||
| 0,7 | |||||||
| 3. | 0,6 | ||||||
| 0,3 | |||||||
| 0,7 | |||||||
| 0,2 | |||||||
| 0,8 | |||||||
| 0,5 | |||||||
| 4. | 0,4 | ||||||
| 0,3 | |||||||
| 0,6 | |||||||
| 0,7 | |||||||
| 0,4 | |||||||
| 0,6 | |||||||
| 5. | 0,3 | ||||||
| 0,7 | |||||||
| 0,2 | |||||||
| 0,8 | |||||||
| 0,5 | |||||||
| 0,4 |
Продолжение табл. 5.1
| № Вар. | № Подвар. | № Дан. |  , кг , кг |  , кг , кг | 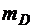 , кг , кг | M, Hм | F, Н | |
| 6. | 0,3 | |||||||
| 0,6 | ||||||||
| 0,7 | ||||||||
| 0,6 | ||||||||
| 0,3 | ||||||||
| 0,7 | ||||||||
| 7. | 0,2 | |||||||
| 0,8 | ||||||||
| 0,5 | ||||||||
| 0,4 | ||||||||
| 0,3 | ||||||||
| 0,6 | ||||||||
| 8. | 0,7 | |||||||
| 0,3 | ||||||||
| 0,7 | ||||||||
| 0,2 | ||||||||
| 0,8 | ||||||||
| 0,5 | ||||||||
| 9. | 0,4 | |||||||
| 0,3 | ||||||||
| 0,6 | ||||||||
| 0,7 | ||||||||
| 0,4 | ||||||||
| 0,6 | ||||||||
| 10. | 0,3 | |||||||
| 0,7 | ||||||||
| 0,2 | ||||||||
| 0,8 | ||||||||
| 0,5 | ||||||||
| 0,4 |
Продолжение табл. 5.1
| № Вар. | № Подвар. | № Дан. |  , кг , кг |  , кг , кг | 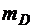 , кг , кг | M, Hм | F, Н |
| 11. | 0,6 | ||||||
| 0,7 | |||||||
| 0,6 | |||||||
| 0,3 | |||||||
| 0,7 | |||||||
| 0,2 | |||||||
| 12. | 200- | 0,8 | |||||
| 0,5 | |||||||
| 0,4 | |||||||
| 0,3 | |||||||
| 0,6 | |||||||
| 0,4 | |||||||
| 13. | 0,3 | ||||||
| 0,6 | |||||||
| 0,7 | |||||||
| 0,3 | |||||||
| 0,7 | |||||||
| 0,2 | |||||||
| 14. | 0,8 | ||||||
| 0,5 | |||||||
| 0,4 | |||||||
| 0,3 | |||||||
| 0,6 | |||||||
| 0,7 | |||||||
| 15. | 0,4 | ||||||
| 0,6 | |||||||
| 0,3 | |||||||
| 0,7 | |||||||
| 0,2 | |||||||
| 0,8 |
Продолжение табл. 5.1
| № Вар. | № Подвар. | № Дан. |  , кг , кг |  , кг , кг | 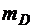 , кг , кг | M, Hм | F, Н |
| 16. | 0,5 | ||||||
| 0,4 | |||||||
| 0,3 | |||||||
| 0,6 | |||||||
| 0,7 | |||||||
| 0,6 | |||||||
| 17. | 0,3 | ||||||
| 0,7 | |||||||
| 0,2 | |||||||
| 0,8 | |||||||
| 0,5 | |||||||
| 0,4 | |||||||
| 18. | 0,3 | ||||||
| 0,6 | |||||||
| 0,4 | |||||||
| 0,3 | |||||||
| 0,6 | |||||||
| 0,7 | |||||||
| 19. | 0,3 | ||||||
| 0,7 | |||||||
| 0,2 | |||||||
| 0,8 | |||||||
| 0,5 | |||||||
| 0,4 | |||||||
| 20. | 0,3 | ||||||
| 0,6 | |||||||
| 0,7 | |||||||
| 0,4 | |||||||
| 0,6 | |||||||
| 0,3 |
Продолжение табл. 5.1
| № Вар. | № Подвар. | № Дан. |  , кг , кг |  , кг , кг | 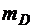 , кг , кг | M, Hм | F, Н |
| 21. | 0,7 | ||||||
| 0,2 | |||||||
| 0,8 | |||||||
| 0,5 | |||||||
| 0,4 | |||||||
| 0,3 | |||||||
| 22. | 0,6 | ||||||
| 0,7 | |||||||
| 0,6 | |||||||
| 0,3 | |||||||
| 0,7 | |||||||
| 0,2 | |||||||
| 23. | 0,8 | ||||||
| 0,5 | |||||||
| 0,4 | |||||||
| 0,3 | |||||||
| 0,6 | |||||||
| 0,7 | |||||||
| 24. | 0,2 | ||||||
| 0,8 | |||||||
| 0,5 | |||||||
| 0,4 | |||||||
| 0,3 | |||||||
| 0,6 | |||||||
| 25. | 0,7 | ||||||
| 0,6 | |||||||
| 0,3 | |||||||
| 0,7 | |||||||
| 0,2 | |||||||
| 0,8 |
Окончание табл. 5.1
| № Вар. | № Подвар. | № Дан. |  , кг , кг |  , кг , кг | 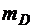 , кг , кг | M, Hм | F, Н |
| 26. | 0,5 | ||||||
| 0,4 | |||||||
| 0,3 | |||||||
| 0,6 | |||||||
| 0,7 | |||||||
| 0,4 | |||||||
| 27. | 0,6 | ||||||
| 0,3 | |||||||
| 0,7 | |||||||
| 0,2 | |||||||
| 0,8 | |||||||
| 0,5 | |||||||
| 28. | 0,4 | ||||||
| 0,3 | |||||||
| 0,6 | |||||||
| 0,7 | |||||||
| 0,6 | |||||||
| 0,3 | |||||||
| 29. | 0,7 | ||||||
| 0,2 | |||||||
| 0,8 | |||||||
| 0,5 | |||||||
| 0,4 | |||||||
| 0,3 | |||||||
| 30. | 0,6 | ||||||
| 0,7 | |||||||
| 0,3 | |||||||
| 0,7 | |||||||
| 0,2 | |||||||
| 0,8 |
 |  |
 |  |
 |  |
| Рис. 5.1 | |
 | 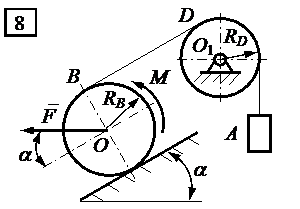 |
 | 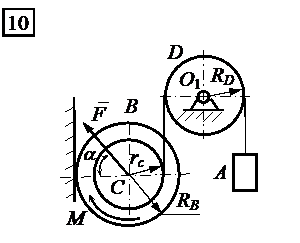 |
 |  |
| Продолжение рис. 5.1 | |
 |  |
 |  |
 |  |
| Продолжение рис. 5.1 | |
 |  |
 |  |
 |  |
| Продолжение рис. 5.1 | |
 |  |
 |  |
 |  |
| Окончание рис. 5.1 |
5.3 Пример выполнения задания
5.3.1. Условие примера
Рассматривается движение механической системы, изображенной на рис. 5.2. Даны следующие значения параметров: 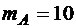 кг,
кг,  кг,
кг,  кг,
кг,  Н,
Н, 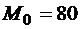 Нм,
Нм,
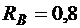 м,
м, 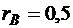 м,
м, 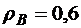 м,
м, 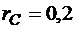 м,
м, 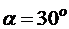 ,
,  ,
, 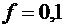 ,
,  м,
м, 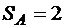 м,
м,  м/с2.
м/с2.
Определить скорость  и ускорение
и ускорение 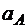 тела А.
тела А.
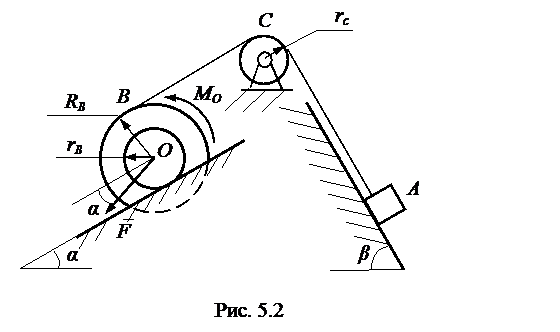
5.3.2. Решение примера
Равенство, выражающее теорему об изменении кинетической энергии механической системы, имеет вид
 , (5.1)
, (5.1)
где  и
и 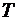 - кинетическая энергия системы в начальном и конечном положениях,
- кинетическая энергия системы в начальном и конечном положениях,
 и
и  - суммарные работы внутренних и внешних сил, приложенных к системе, при ее переходе из первого положения во второе.
- суммарные работы внутренних и внешних сил, приложенных к системе, при ее переходе из первого положения во второе.
На рис. 5.3 условно изображены начальное и конечное положения данной системы.

Согласно условию задачи система начинает движение из состояния покоя, поэтому  .
.
Кроме того, поскольку тела, образующие систему, абсолютно твердые и трос не растягивается, то 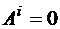 .
.
Таким образом, равенство (5.1) запишется
 . (5.2)
. (5.2)
Кинетическая энергия системы равна

Груз А движется поступательно со скоростью  , поэтому
, поэтому
 (5.3)
(5.3)
Шкив С вращается с угловой скоростью  , следовательно,
, следовательно,
 (5.4)
(5.4)
Момент инерции 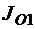 шкива С относительно оси, проходящей через точку О1, определяется по формуле:
шкива С относительно оси, проходящей через точку О1, определяется по формуле:
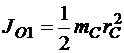 (5.5)
(5.5)
Угловая скорость  шкива С равна
шкива С равна
 . (5.6)
. (5.6)
Подставляя выражения (5.5) и (5.6) в равенство (5.4), получаем:
 . (5.7)
. (5.7)
Кинетическую энергию колеса В, совершающего плоское движение, находим по формуле:
 . (5.8)
. (5.8)
Здесь  - линейная скорость центра О масс колеса В,
- линейная скорость центра О масс колеса В,
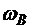 - мгновенная угловая скорость колеса В,
- мгновенная угловая скорость колеса В,
 - момент инерции колеса В относительно оси, проходящей через центр О.
- момент инерции колеса В относительно оси, проходящей через центр О.
На рисунке 5.3 буквой  обозначен мгновенный центр скоростей колеса В. Очевидно, что мгновенная угловая скорость колеса В
обозначен мгновенный центр скоростей колеса В. Очевидно, что мгновенная угловая скорость колеса В
 .
.
Но для нормальной работы системы скорости  , а
, а  , тогда
, тогда
 . (5.9)
. (5.9)
Скорость центра О колеса В равна
 . (5.10)
. (5.10)
Момент инерции колеса В равен
 . (5.11)
. (5.11)
После подстановки выражений (5.9) и (5.10) в формулу (5.8), получаем:
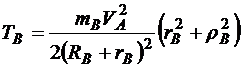 . (5.12)
. (5.12)
Далее, суммируя выражения (5.3),(5.7) и (5.12), окончательно имеем
 . (5.13)
. (5.13)
Внешние силы, действующие на рассматриваемую механическую систему, показаны на рисунке 5.3. Причем сила трения скольжения действующая на тело А имеет максимальное значение, которое находится по формуле Кулона:
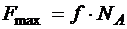 . (5.14)
. (5.14)
Здесь  - нормальная реакция плоскости находится по формуле
- нормальная реакция плоскости находится по формуле
 . (5.15)
. (5.15)
Суммарная работа внешних сил действующих на рассматриваемую механическую систему равна
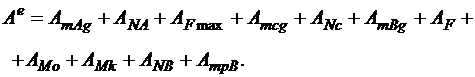 (5.16)
(5.16)
Работа силы тяжести 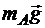 тела А:
тела А:
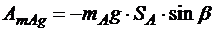 . (5.17)
. (5.17)
Работа максимальной силы трения скольжения  тела А:
тела А:
 .
.
С учетом равенств (5.14) и (5.15), последнее выражение примет вид
 . (5.18)
. (5.18)
Работа нормальной реакции  :
:
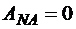 , (5.19)
, (5.19)
так как 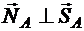 .
.
Точки приложения сил 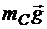 и
и  не перемещаются, поэтому
не перемещаются, поэтому
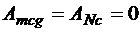 . (5.20)
. (5.20)
Работа силы тяжести 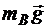 колеса В:
колеса В:
 . (5.21)
. (5.21)
Работа постоянной силы 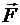 :
:
 . (5.22)
. (5.22)
Работа постоянного момента  :
:
 . (5.23)
. (5.23)
Работа нормальной реакции  наклонной плоскости:
наклонной плоскости:
 , (5.24)
, (5.24)
так как эта сила перпендикулярна вектору перемещения ее точки приложения.
Сила трения скольжения колеса В приложена в мгновенном центре скоростей колеса В, поэтому:
 . (5.25)
. (5.25)
Работа максимально момента трения качении 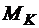 :
:
 . (5.26)
. (5.26)
Величина максимального момента трения качения дается формулой
 . (5.27)
. (5.27)
Для определения зависимостей перемещения  центра О и угла
центра О и угла  поворота колеса В от перемещения
поворота колеса В от перемещения 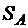 тела А умножим обе части выражений (5.9), (5.10) на
тела А умножим обе части выражений (5.9), (5.10) на 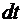 . Имеем
. Имеем
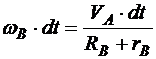 ,
, 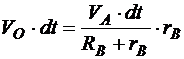 .
.
Или
 ,
,  .
.
Интегрируя обе части последних двух уравнений, получаем
 ,
,  . (5.28)
. (5.28)
Подставляя выражения (5.17)-(5.26) в сумму (5.16), с учетом формул (5.27), (5.28), имеем
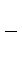

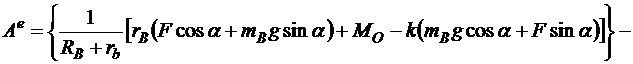

 (5.29)
(5.29)
Тогда равенство (5.2) с учетом выражений (5.13) и (5.29) примет вид




