Физика атома. Спектры атомов

1. Полная энергия электрона в состоянии, характеризуемом главным квантовым числом n

, (3)

где E_i = Rhc– энергия ионизации атома водорода;Z– порядковый номер элемента в таблице Менделеева;Е_i=13,5эВ.

2. Энергия, излучаемая или поглощаемая атомом водорода или водородоподобным ионом

E = h ,

где n₁ и n₂ – главные квантовые числа, соответствующие энергетическим состояниям, между которыми совершается переход электрона.

3. Сериальная формула для определения длины волны спектра излучения атома водорода (или водородоподобного иона)

= RZ² ,

где l– длина волны фотона;R– постоянная Ридберга.

Примеры решения задач

Задача 1

Атом водорода перешел из возбужденного состояния, характеризуемого главным квантовым числом, равным трем, в основное. Определить возможные спектральные линии в спектре излучения водорода. Найти максимально возможную энергию фотона.

Дано:	Решение:
n1 = 1 n2 = 3	n = 3   n = 2     n = 1 Рис. 1
- ? - ?

Из рисунка видно, что при переходе атома из состояния, характеризуемого главным квантовым числом n=3, в основное (n=1), возможно излучение трех спектральных линий.

Для определения длины волны воспользуемся сериальной формулой для водородоподобных ионов

,

где l– длина волны фотона; R– постоянная Ридберга; Z– заряд ядра в относительных единицах (при Z=1 формула переходит в сериальную формулу для водорода); n₁ – главное квантовое число состояния, в которое перешел атом; n₂– главное квантовое число исходного состояния.

Найдем длину волны линии, излученной при переходе атома из состояния n₂=3 в состояние n₁=2, приняв постоянную Ридберга м^-1:

, мкм.

Аналогично находим длину волны спектральной линии, излученной атомом при переходе из состояния n₂ =2 в состояние n₁=1.

, мкм.

При переходе из состояния n₂ =3 в состояние n₁ =1 длина волны линии равна

, мкм.

Энергия фотона определяется из выражения

_ф = hc/ ,

гдеh–постоянная Планка, h= 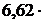10^-34 Дж , с–скорость света в вакууме,с= 10⁸м/с.

Максимальная энергия фотона соответствует минимальной длине волны, следовательно

_ф = hc/ .

Элементы квантовой механики

1. Длина волны де Бройля

,

где p– импульс частицы.

2. Если кинетическая энергия частицы много меньше энергии покоя (Е_k<<E₀), то для определения импульса частиц можно пользоваться классическим выражением, т.е.

p = mv = ,

где кинетическая энергия частицы .

3. Если кинетическая энергия частицы E_k 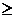E₀, то импульс частицы следует вычислять по формуле релятивистской механики, т.е.

,

где Е_о–энергия покоя частицы;Е_к– кинетическая энергия частицы, равная

Е_к= m₀c² ,

где m₀– масса покоя частицы;v– скорость частицы.

4. Соотношения неопределенностей:

а) для координаты и импульса ∆p_x∆x≥ћ/2,

где – неопределенность проекции импульса на ось x;

– неопределенность координаты x;

б) для энергии и времени ∆E∆t≥ћ/2,

где – неопределенность энергии; t– время жизни квантовой системы в данном энергетическом состоянии.

Примеры решения задач

Задача 1

Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля для двух случаев: 1) U₁ = 51 B; 2) U₂ = 510 кВ.

Дано:	Решение:
U1 = 51 B U2 = 510 кВ = 105 В	Длина волны де Бройля для частицы зависит от ее импульса р и определяется формулой , (1) где h – постоянная Планка.

Импульс частицы можно определить, если известна ее кинетическая энергия Е_к. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше энергии ее покоя) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы):

- в нерелятивистском случае

,(2)

- в релятивистском случае

,(3)

где – энергия покоя частицы.

Формула (1) с учетом соотношений (2) и (3) запишется:

- в нерелятивистском случае

, (4)

- в релятивистском случае

. (5)

Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U₁ = 51 В и U₂ = 510 кВ, с энергией покоя электрона и, в зависимости от этого, решим, которую из формул – (4) или – (5) следует применить для вычисления длины волны де Бройля.

Как известно, кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, равна

E_к = eU.

В первом случае

Е_к = eU₁ = 51 эВ = 10^-4 МэВ, что много меньше энергии покоя электрона, равной МэВ.

Следовательно, в этом случае можно применить формулу (4). Для упрощения расчетов заметим, что Е_к= 10^-4m₀c². Подставив это выражение в формулу (4), перепишем ее в виде

.

Учитывая, что h/m_oc есть комптоновская длина волны , получим:

.

Так как =2,43 пм, то

пм = 171 пм.

Во втором случае кинетическая энергия

E_к = eU₂ = 510 кэВ = 0,51 МэВ,

т.е. равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (5). Учитывая, что Е_к= 0,51МэВ = m_oc², по формуле (5) найдем

,

или .

Подставив значение и произведя вычисления, получим:

пм = 1,40 пм.

Задача 2

Кинетическая энергия электрона в атоме водорода составляет величину порядка 10 эВ. Используя соотношение неопределенностей, оценить минимальные размеры атома.

Дано:	Решение:
Ек= 10 эВ	Соотношение неопределенностей для координаты и импульса имеет вид ∆px∆x ≥ ħ/2, где ∆px – неопределенность импульса частицы (электрона); ∆x – неопределенность
lmin - ?

координаты частицы (в данном случае электрона); ħ = h/2p– приведенная постоянная Планка h.

Из соотношения неопределенностей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в пределах области с неопределенностью

Δx = l / 2.

Cоотношение неопределенностей можно записать в этом случае в виде

,

откуда

Физически разумная неопределенность импульса Δp, во всяком случае, не должна превышать значение самого импульса p, т. е. Δp ≤ p.

Импульс р связан с кинетической энергией Е_к соотношением

р = .

Заменим р значением (такая замена не увеличит l). Перейдем к равенству

.

Подставив числовые значения и произведя вычисления, получим:

l_min = м = 10^-10 м = 116 пм.

Задача 3. Оценить относительную ширину испускаемой спектральной линии, длина волны которой составляет 0,6 мкм, при переходе атома из возбужденного в основное состояние. Время жизни атома в возбужденном состоянии оставляет приблизительно .

Дано:	Решение:
∆t=	Выразим ширину испускаемой спектральной линии через энергию фотона с помощью формулы Планка: , где – частота фотона;h – постоянная Планка; ε – энергия фотона, откуда .

Частота испускаемого фотона связана с длиной волны соотношением

,

где с – скорость света в вакууме.

Искомая величина равна .

Для нахождения Δε воспользуемся соотношением неопределенностейдля энергии и времени ∆ε∆t≥ћ/2,

где – неопределенность энергии; t– время жизни атома в возбужденном энергетическом состоянии.

∆ε=ћ/2∆t.

Подставим ∆ε в искомую величину, получим:

.

Подставим числовые значения и находим

.

Физика твердого тела

1. Удельная электропроводность полупроводника

e(nu_n + pu_p),

где е – заряд электрона;n и p– концентрация носителей заряда (подвижных электронов и дырок);u_n и u_p– подвижности электронов и дырок.

В случае проводимости одного типа одним из слагаемых в выражении (1) можно пренебречь. Для чистого, беспримесного полупроводника проводимость называется собственной и в формуле для следует положить n = p.

2. Зависимость собственной удельной электропроводности полупроводника от температуры

,

где Е– ширина запрещенной зоны полупроводника; – константа, почти не зависящая от температуры; k– постоянная Больцмана.

3. Холловская разность потенциалов равна

U_н = R_н I,

где В– индукция магнитного поля;а– толщина образца; I– сила тока в образце; – постоянная Холла.

4. Для полупроводника с кристаллической решеткой типа алмаза (Ge, Si) с примесной проводимостью одного типа постоянная Холла равна

.

Примеры решения задач

Задача 1

До какой температуры нужно нагреть образец из арсенида галлия, находящегося при температуре 0 , чтобы его проводимость возросла в 4 раза?

Дано:	Решение:
Т = 273К	Удельная проводимость полупроводников связана с температурой соотношением ,
Т = ?

где постоянная; ширина запрещенной зоны; k– постоянная Больцмана.

Таким образом, .

Прологарифмируем выражение и получим:

,

откуда

.

Полагая для арсенида галлия DЕ=1,43 эВ, произведем вычисления

.

Задача 2

Некоторый примесный полупроводник имеет решетку типа алмаза и обладает только дырочной проводимостью. Определить концентрацию носителей и их подвижность, если постоянная Холла равна м³/Кл. Удельная проводимость полупроводника 110 .

Дано:	Решение:
м3/Кл = 110 Ом-1	Концентрация р дырок связана с постоянной Холла, которая для полупроводников с решеткой типа алмаза, обладающих носителями только одного знака, выражается формулой
np - ? up - ?

R_н= ,

где е – элементарный заряд.

Отсюда

. (1)

Запишем все величины в единицах СИ: е = 10^-19 Кл; 10^-4 м³/Кл.

Подставим числовые значения величин в формулу (1) и произведем вычисления

.

Удельная проводимость полупроводников выражается формулой

= e(nu_n+ pu_p), (2)

где n и p– концентрации электронов и дырок; u_n и u_p– их подвижности.

При отсутствии электронной проводимости первое слагаемое в скобках равно нулю и формула (2) примет вид

= epu_p.

Отсюда искомая подвижность

u_p= . (3)

Подставим в (3) выражение р по формуле (1)

u_p= . (4)

Подставив в (4) значения и и произведя вычисления, получим:

_.