Основы механики жидкостей и газов

Предмет гидроаэромеханики

Гидроаэромеханика – раздел механики, посвящённый изучению равновесия и движения жидких и газообразных сред и их взаимодействия между собой и обтекаемыми ими твёрдыми телами.

Движение несжимаемой жидкости изучается в гидродинамике, а газов – в аэродинамике.

Газ и жидкость в гидроаэромеханике

Газ (от греч. chaos – хаос) – агрегатное состояние вещества, в котором его частицы не связаны или слабо связаны силами взаимодействия и движутся свободно, занимая весь предоставленный им объём.

В отличие от твёрдых тел и жидкостей объём газа существенно зависит от давления и температуры.

Жидкость – это агрегатное состояние вещества, промежуточное между твёрдым и газообразным.

Жидкости присущи некоторые черты твёрдого тела (сохраняет свой объём, образует поверхность, обладает определённой прочностью на разрыв) и газа (принимает форму сосуда, в котором находится, может непрерывно переходить в газ); в то же время она обладает рядом только ей присущих особенностей, из которых наиболее характерной является текучесть.

Нормальные жидкости макроскопически однородны и изотропны при отсутствии внешних воздействий. Последнее так же сближает их с газами.

В гидроаэромеханике жидкости и газы рассматривают как сплошную, непрерывную среду, отвлекаясь от их молекулярного строения.

Хотя свойства жидкостей и газов во многом отличаются, в ряде механических явлений их поведение описывается одинаковыми параметрами и идентичными уравнениями.

Предмет гидроаэромеханики

Гидростатика – раздел гидроаэромеханики, в котором изучаются равновесие жидкости и воздействие покоящейся жидкости на погруженные в неё тела, жидкость при этом считается практически несжимаемой.

Аэростатика – раздел гидроаэромеханики, в котором изучается равновесие газообразных сред, в основном атмосферы.

При этом необходимо учитывать, что сжимаемость газов во много раз превосходит сжимаемость жидкостей.

Основными законами гидроаэростатики являются закон Паскаля[18] и закон Архимеда[19].

Давление покоящейся жидкости (газа). Закон Паскаля

Закон был установлен экспериментально французским учёным Б.Паскалем в 1648 г.: давление, производимое на покоящуюся жидкость (газ) внешними силами передаётся жидкостью (газом) одинаково во всех направлениях (рис. 86): P = , Па, где P – это давление, F – приложенная сила, S – площадь поверхности, на которую действует сила давления .

Рис. 86.

Это утверждение объясняется подвижностью частиц жидкостей и газов во всех направлениях. Из формулы мы видим, что при увеличении силы воздействия при той же площади сосуда давление на его стенки будет увеличиваться.

Действительно, если в покоящуюся жидкость (газ) поместить небольшую тонкую пластинку, то части жидкости (газа), находящиеся по разные стороны от неё, будут действовать на каждый её элемент ∆S с силами ∆ , которые независимо от того, как пластинка ориентирована, будут равны по модулю и направлены перпендикулярно площадке ∆S, т.к. наличие касательных сил привело бы частицы жидкости в движение (рис. 87).

Рис. 87.

Для сжимаемых жидкостей (газов) закон Паскаля, вообще говоря, несправедлив.

Закон Паскаля неприменим в случае движущейся жидкости (газа), а также в случае, когда жидкость (газ) находится в гравитационном поле; так, известно, что атмосферное и гидростатическое давление уменьшается с высотой.

На основе закона Паскаля работают различные гидравлические устройства: тормозные системы, гидравлические прессы и др., например, гидравлический мультипликатор (рис. 88), гидравлический пресс (рис. 89).

Гидравлический мультипликатор предназначен для увеличения давления (Р₂ > Р₁, так как при одинаковой силе давления S₁> S₂ ).

Рис. 88.

Рис. 89.

Гидростатическое давление

Рассмотрим равновесие однородной жидкости, находящейся в поле тяготения Земли. На каждую частицу жидкости, находящейся в поле тяготения Земли, действует сила тяжести. Жидкости и газы передают по всем направлениям не только оказываемое на них внешнее давление, но и то давление, которое существует внутри их благодаря весу собственных частей. Верхние слои жидкости давят на средние слои, те - на нижние, а последние - на дно.

Давление, оказываемое покоящейся жидкостью, называется гидростатическим.

Получим формулу для расчета гидростатического давления жидкости на произвольной глубине h в окрестности точки А ( рис. 90).

Рис. 90.

Сила давления, действующая в этом месте со стороны вышележащего узкого вертикального столба жидкости, может быть выражена двумя способами:
во-первых, как произведение давления в основании этого столба на площадь его сечения:
F = Р S;

во-вторых, как вес того же столба жидкости, т. е. произведение массы жидкости на ускорение свободного падения g: F = mg = 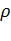Sgh.

Приравняем оба выражения для силы давления: PS = 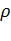Sgh.

Разделив обе части этого равенства на площадь S, найдем давление жидкости на глубине h: P = gh,

где P = 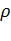gh — гидростатическое давление, — плотность жидкости, h — высота столба жидкости.

Мы получили формулу гидростатического давления:гидростатическое давление на любой глубине внутри жидкости не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободного падения и глубины, на которой рассматривается давление.

Одно и то же количество воды, находясь в разных сосудах, может оказывать разное давление на дно. Поскольку это давление зависит от высоты столба жидкости, то в узких сосудах оно будет больше, чем в широких. Благодаря этому даже небольшим количеством воды можно создать очень большое давление.

Давление жидкости на дно не зависит от формы сосуда, а определяется только высотой уровня жидкости и ее плотностью. Во всех случаях, приведенных на рисунке 91, давление жидкости на дно сосудов одинаково.

Рис. 91.

Жидкость давит на данной глубине одинаково по всем направлениям — не только вниз, но и вверх, и в стороны. Следовательно, давление на стенку на данной глубине будет таким же, как и давление на горизонтальную площадку, расположенную на той же глубине.

Если над свободной поверхностью жидкости создается давление P₀ то давление в жидкости на глубине будет: P = P₀ + 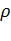gh.

Силы давления на дно и на стенки можно рассчитать по формулам:

F= 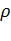ghS — сила давления жидкости на горизонтальное дно, где S_д — площадь дна;

F_ст. = S_ст. — сила давления жидкости на боковую прямоугольную вертикальную стенку сосуда, где S_ст. — площадь стенки.

Пример.В покоящейся жидкости свободная поверхность жидкости всегда горизонтальна. Нередко встречаются случаи, когда жидкость, покоясь относительно сосуда, движется вместе с ним. Если при этом сосуд движется равномерно и прямолинейно, то свободная поверхность жидкости будет горизонтальна. Но если сосуд движется с ускорением, то ситуация меняется и возникают вопросы о форме свободной поверхности жидкости, о распределении давления в ней.

Так, в случае горизонтального движения сосуда с ускорением в поле тяготения Земли любая часть жидкости массой m движется с тем же ускорением под действием равнодействующей силы давления , действующей со стороны остальной жидкости и силы тяжести m (рис. 92).

Рис. 92.

Основное уравнение динамики: m = + m .

В результате свободная поверхность жидкости не будет горизонтальна, а образует с горизонтом угол 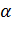, который можно легко найти, если спроецировать основное уравнение динамики на горизонтальную и вертикальную оси:

N 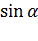= ma; N = mg.

Отсюда: tg = .

Давление на горизонтальную поверхность (горизонтальное дно) будет возрастать в направлении, противоположном ускорению.

Закон Архимеда. Условия плавания тел