Уравнение Менделеева – Клапейрона 98

Барометрическая формула. Распределение Больцмана 99

Средняя длина свободного пробега молекул 101

II. Термодинамика 103

Термодинамический метод 103

Внутренняя энергия 103

Обратимые и необратимые процессы 105

Работа расширения идеального газа. Графическое

Изображение работы 106

Круговые процессы (циклы) 107

Первое начало термодинамики 108

Полная энергия. Закон сохранения полной энергии 110

Теплоёмкость 110

Применение первого начала термодинамики к

Изопроцессам идеального газа 113

Применение первого закона термодинамики к

Адиабатному процессу 115

Термический КПД для кругового процесса 117

Тепловые двигатели 117

Цикл Карно 121

Второе начало термодинамики 123

Энтропия 125

Статистическая интерпретация второго начала

Термодинамики 131

Предисловие

Учебное пособие предназначено для курсантов и студентов всех специальностей МГТУ.

Цель данного учебного пособия – помочь курсантам и студентам при изучении теоретического курса механики, молекулярной физики и термодинамики.

Основной материал пособия набран обычным шрифтом, материал вспомогательного, информационного характера – более мелким шрифтом.

В конце к4аждого раздела приводятся контрольные вопросы для самопроверки, а также разобраны примеры решения некоторых задач.

Содержание пособия в основном соответствует требованиям ГОС ВПО по физике для студентов-бакалавров технических направлений и специальностей.

Часть I. МЕХАНИКА

Предмет механики

Механика – наука о движении материальных тел и происходящих при этом взаимодействиях между ними.

Классическая механика рассматривает движение макроскопических тел, происходящее со скоростями с, где с = 3•10⁸ м/с – скорость света в вакууме.

Механическое движение. Основные понятия механики

Механическое движение – изменение положения тел (или их частей) в пространстве относительно других тел.

Из этого определения следует, что механическое движение – движение относительное.

Тело, по отношению к которому рассматривается данное механическое движение, называется телом отсчёта.

Система отсчёта — это совокупность тела отсчёта, системы координат и системы отсчёта времени, связанных с этим телом, по отношению к которому изучается движение (или равновесие) каких-либо других материальных точек или тел (рис.1).

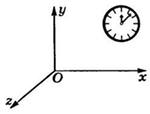
Рис.1.

Выбор системы отсчёта зависит от целей исследования. При кинематических исследованиях все системы отсчёта равноправны. В задачах динамики преимущественную роль играют инерциальные системы отсчёта.

Инерциальная система отсчёта (и.с.о.) – система отсчёта, в которой справедлив закон инерции: материальная точка, когда на неё не действуют никакие силы (или действуют силы взаимно уравновешенные), находится в состоянии покоя или равномерного прямолинейного движения.

Всякая система отсчёта, движущаяся по отношению к и. с. о. поступательно, равномерно и прямолинейно, есть также и. с. о. Следовательно, теоретически может существовать сколько угодно равноправных и. с. о., обладающих тем важным свойством, что во всех таких системах законы физики одинаковы (так называемый принцип относительности). Если система отсчёта движется по отношению к и. с. о. неравномерно и прямолинейно, то она являетсянеинерциальнойи закон инерции в ней не выполняется. Объясняется это тем, что по отношению к неинерциальной системе отсчёта материальная точка будет иметь ускорение даже при отсутствии действующих сил вследствие ускоренного поступательного или вращательного движения самой системы отсчёта. Понятие об и. с. о. является научной абстракцией. Реальная система отсчёта связывается всегда с каким-нибудь конкретным телом (Землёй, корпусом корабля или самолёта и т. п.), по отношению к которому и изучается движение тех или иных объектов. Поскольку в природе нет неподвижных тел (тело, неподвижное относительно Земли, будет двигаться вместе с нею ускоренно по отношению к Солнцу и звёздам и т. д.), то любая реальная система отсчёта является неинерциальной и может рассматриваться как и. с. о. лишь с той или иной степенью приближения. С очень высокой степенью точности и. с. о. можно считать так называемую гелиоцентрическую (звёздную) систему с началом в центре Солнца (точнее, в центре масс Солнечной системы) и с осями, направленными на три звезды. Для решения большинства технических задач и. с. о. практически может служить система, жестко связанная с Землёй, а в случаях, требующих большей точности (например, в гироскопии), — с началом в центре Земли и осями, направленными на звёзды. При переходе от одной и. с. о. к другой в классической механике Ньютона для пространственных координат и времени справедливы преобразования Галилея, а в релятивистской механике (т. е. при скоростях движения, близких к скорости света) — преобразования Лоренца.

Материальная точка – тело, размерами, формой и внутренней структурой которого можно пренебречь в условиях данной задачи.

Материальная точка – объект абстрактный.

Абсолютно твёрдое тело (АТТ) – тело, расстояние между двумя любыми точками которого остаётся неизменным (деформацией тела можно пренебречь).

АТТ – объект абстрактный.

Финитное движение – движение в ограниченной области пространства, инфинитное движение – неограниченное в пространстве движение.

Положение точки А в пространстве задается радиус – вектором или тремя его проекциями на оси координат (рис.2).

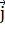Следовательно, закон движения – это зависимость радиус-вектора от времени или зависимость координат во времени, где = x + y + z 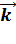- радиус-вектор, x, y, z – координаты точки;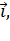 , – единичные орты[1]:

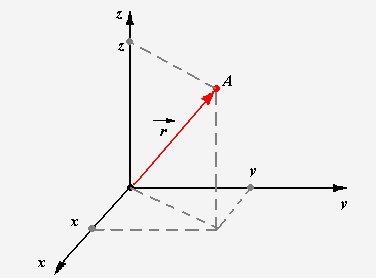
Рис.2.

= r(t) или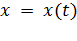

Кинематика

Кинематика – раздел механики, посвящённый изучению законов движения тел без учёта их масс и действующих сил.

Основные понятия кинематики

Траектория (лат. trajectorius – относящийся к перемещению)– непрерывная линия, которую описывает точка при своём движении (рис.4)

Рис.4.

Если траектория прямая линия, то движение называется прямолинейным, если кривая линия – то криволинейным. Траектория – понятие относительное, т.к. вид траектории зависит от выбранной системы отсчёта. Вид траектории зависит так же от наложенных связей.

Например, по отношению к Земле (если пренебречь её суточным вращением) траектория свободной материальной точки, отпущенной без начальной скорости и движущейся под действием силы тяжести, будет прямая линия (вертикаль), а если точке сообщить начальную скорость 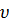₀ не направленную вдоль вертикали, то при отсутствии сопротивления воздуха её траектория будет парабола (рис. 5).

Рис. 5. Параболическая траектория.

Путь (S, l)– скалярная физическая величина, равная длине участка траектории, пройдённого материальной точкой за рассматриваемый промежуток времени; в СИ: [S, l] = м (метр[2]).

Перемещение(∆ 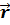) – вектор, соединяющий положение движущейся точки в начале и конце некоторого промежутка времени (рис.5);в СИ: [(∆ 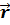]= м.

Рис.6.

Из рис. 7 видно, что ∆ 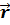= 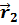– 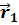,причём S, где S – длина пути:

- перемещение, ABCD – путь.

Рис.7.

Пример .Движение точки задано уравнениями:

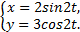
Написать уравнение траектории движения точки и определить её координаты через 1с после начала движения.

Решение

Чтобы исключить время, параметр t, найдём из первого уравнения sin2t = x/2, из второго cos2t = y/3. Затем возведём в квадрат и сложим. Так как sin²2t + cos²2t=1, получим + 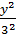= 1. Это уравнение эллипса с полуосями 2 см и 3 см (рис.8).

Начальное положение точки M₀ (при t = 0) определяется координатами x₀ =0, y₀=3 см. Через 1 сек. Точка будет в положении M₁ с координатами: x₁= 2sin2 = 2∙0,91= 1,82 см, y₁=2cos2=3∙(-0,42)=-1,25 см.

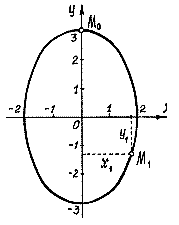
Рис.8.

Время (t) – одна из категорий (наряду с пространством), обозначающая форму существования материи; форма протекания физических и психических процессов; выражает порядок смены явлений; условие возможности изменения, а также одна из координат пространства-времени, вдоль которой протянуты мировые линии физических тел; в СИ: [t] = c – секунда[3].

В классической физике неявно предполагалось, что время величина абсолютная, т.е. одинаково во всех инерциальных системах отсчёта (t = t′). Однако, в специальной теории относительности была доказана зависимость времени от выбора инерциальной системы отсчёта: t′ = 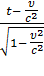, где t – время, измеренное по часам наблюдателя, движущегося вместе с системой отсчёта. Отсюда следовал вывод об относительности одновременности, а именно: в отличие от классической физики, где предполагалось, что события одновременные в одной инерциальной системе отсчёта одновременны и в другой инерциальной системе отсчета, в релятивистском[4] случае пространственно разобщённые события одновременные в одной инерциальной системе отсчёта могут быть неодновременными в другой системе отсчёта.

З.2. Скорость

Скорость(часто обозначается , 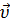или от англ. velocity или фр. vitesse) – векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта.

Мгновенная скорость – векторная величина, равная первой производной радиус вектора 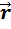движущейся точки по времени (скорость тела в данный момент времени или в данной точке траектории):

= = , ( ).

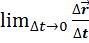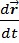Вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки (рис.9).

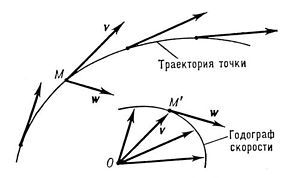
Рис. 9.

В прямоугольной декартовой системе координат:

= + + .

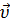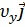В то же время 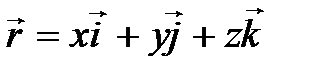, поэтому

= .

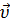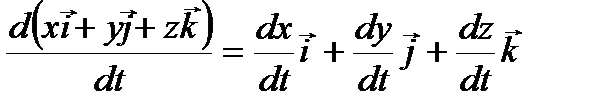Таким образом, координаты вектора скорости – это скорости изменения соответствующей координаты материальной точки:

,

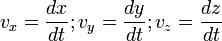или в обозначениях: = =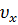

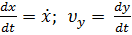Тогда модуль скорости можно представить: =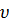

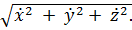
В общем случае путь S отличен от модуля перемещения |Δ 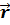|. Одинаково, если рассматривать путь dS, проходимый точкой за малый промежуток времени dt, то dS=|d 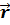|. Поэтому модуль вектора скорости равен первой производной от длины пути по времени: = = .

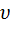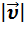Если модуль скорости точки не изменяется с течением времени ( 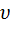= const), то движение называется равномерным.

Для равномерного движения справедливо соотношение: =

Если модуль скорости изменяется со временем ( 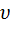= f(t)), то движение называется неравномерным.

Неравномерное движение характеризуется средней скоростью (< 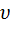>) и ускорением ( ).

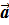Средней путевой скоростью неравномерного движения точки на данном участке ее траектории называется скалярная величина < 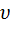>, равная отношению длины этого участка, траектории к продолжительности времени ∆ t прохождения его точкой (рис.10): < 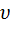> = 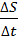, где ∆S – путь, пройдённый точкой за время ∆t.

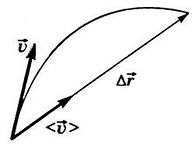
Рис. 10. Мгновенная и средняя скорости.

В общем случае зависимость скорости неравномерного движения от времени изображена на рис.11, где площадь закрашенной фигуры численно равна пройдённому пути S.

Рис. 11.

В классической механике скорость – величина относительная, т.е. преобразуется при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея.

При рассмотрении сложного движения (то есть когда точка или тело движется в одной системе отсчёта, а она движется относительно другой) возникает вопрос о связи скоростей в 2 – х системах отсчёта, который устанавливает классический закон сложения скоростей:

скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно движущейся системы и скорости самой движущейся системы относительно неподвижной:

= ,

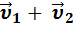где скорость точки относительно неподвижной системы отсчёта, 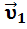–скорость движущейся системы отсчёта относительно неподвижной системы, скорость точки относительно движущейся системы отсчёта.

Пример .

1. Абсолютная скорость мухи, ползущей по радиусу вращающейся граммофонной пластинки, равна сумме скорости её движения относительно пластинки и той скорости, которую имеет точка пластинки под мухой относительно земли (то есть с которой её переносит пластинка за счёт своего вращения).

2. Если человек идёт по коридору вагона со скоростью 5 километров в час относительно вагона, а вагон движется со скоростью 50 километров в час относительно Земли, то человек движется относительно Земли со скоростью 50 + 5 = 55 километров в час, когда идёт по направлению движения поезда, и со скоростью 50 — 5 = 45 километров в час, когда он идёт в обратном направлении. Если человек в коридоре вагона движется относительно Земли со скоростью 55 километров в час, а поезд со скоростью 50 километров в час, то скорость человека относительно поезда 55 — 50 = 5 километров в час.

Если волны движутся относительно берега со скоростью 30 километров в час, и корабль также со скоростью 30 километров в час, то волны движутся относительно корабля со скоростью 30 — 30 = 0 километров в час, то есть относительно корабля они становятся неподвижными.

В релятивистском случае ( 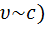применяется релятивистский закон сложения скоростей:

= .

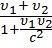Из последней формулы следует, что скорость света – максимальная скорость передачи взаимодействий в природе.

Ускорение

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Ускорение(обычно обозначается ) — производная скорости по времени, векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).

Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,81 м/с каждую секунду, то есть, его ускорение, называемое ускорением свободного падения g = 9,81 м/с².

Производная ускорения по времени, т.е. величина, характеризующая скорость изменения ускорения, называется рывок.

Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:

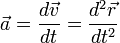, ( м/с²).

Модуль ускорения а величина алгебраическая:

а >0 – движение ускоренное (скорость возрастает по величине);

a < 0 – движение замедленное (скорость уменьшается по величине);

а = 0 – движение равномерное.

Если а = const – движение равнопеременное (равноускоренное или равнозамедленное).

Среднее ускорение

Среднее ускорение < 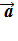> – это отношение изменения скорости к промежутку времени, за который это изменении произошло:

< >= ,

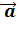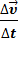где < 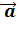>– вектор среднего ускорения.

Направление вектора ускорения совпадает с направлением изменения скорости Δ 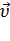= 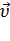- 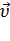₀ (здесь 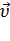₀ – это начальная скорость, то есть скорость, с которой тело начало ускоряться).

В момент времени t₁ тело имеет скорость 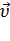₀. В момент времени t₂ тело имеет скорость 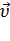(рис.12).Согласно правилу вычитания векторов найдём вектор изменения скорости Δ 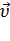= 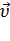- 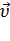₀ . Тогда определить ускорение можно так:

.

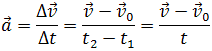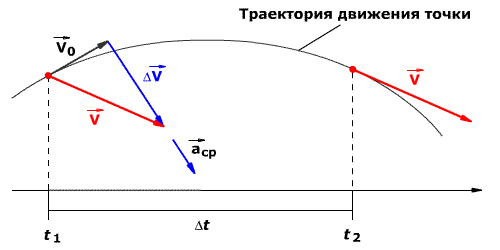
Рис. 12.

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

.

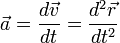Направление ускорения также совпадает с направлением изменения скорости Δ 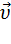при очень малых значениях промежутка времени, за который происходит изменение скорости.

Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта:

a_x = 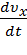= = ; a_y = 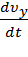= = 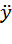; a_z = = = .

т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул: a = ,

= , = , = ,

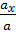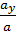где α, β, γ – углы, образуемые вектором ускорения с координатными осями.